斐波那契数-leetcode509-动态规划

1、题目

斐波那契数，通常用 F(n) 表示，形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1

F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给你 n ，请计算 F(n) 。

示例 1：

输入：2

输出：1

解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

输入：3

输出：2

解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：

输入：4

输出：3

解释：F(4) = F(3) + F(2) = 2 + 1 = 3

2、讲解

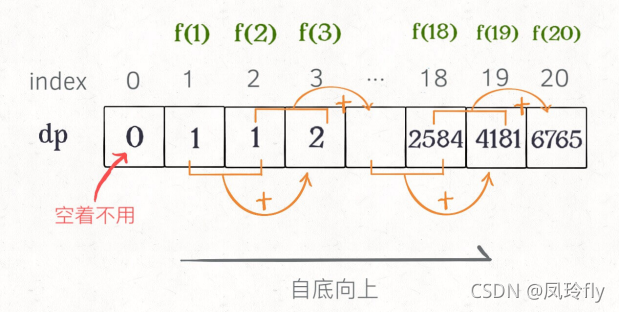
由于斐波那契数存在递推关系，因此可以使用动态规划求解，动态规划的状态转移方程即为F(n) = F(n - 1) + F(n - 2)，边界条件为 F(0)和F(1)

class Solution:
    def fib(self, n: int) -> int:
        if n == 0:
            return 0
        if n <= 2:
            return 1
        dp = [0 for _ in range(n)]
        dp[0] = 0
        dp[1] = 1
        for i in range(2, n):
            dp[i] = dp[i - 1] + dp[i - 2]
        return dp[-1]

复杂度分析

时间复杂度：O(n)

空间复杂度：O(1)

 

欢迎关注我的微信公众号，在你碎片化的时间内也可以学习刷题