merge()这个算法是将两个区间的元素合并(准确的说应该是得到两个已序区间内的所有元素)
OutputIterator merge(InputIterator source1Beg,InputIterator source1End,
InputIterator source2Beg,InputIterator source2End,
OutputIterator destBeg)
OutputIterator merge(InputIterator source1Beg,InputIterator source1End,
InputIterator source2Beg,InputIterator source2End,
OutputIterator destBeg,BinaryPredicate op)
- 两者都是将源区间[ source1Beg, source1End),[ source2Beg,source2End)内的元素合并,使得“以destBeg起始的目标区间”内 含两个源区间的所有元素
- 目标区间的所有元素都将按顺序排列
- 两者都返回目标区间“最后一个被复制元素”的下一位置(即第一个未被覆盖的元素)
- 根据标准,调用者应确保两个源区间一开始就是已序的
- 应确保目标区间足够大,否则需要使用插入型迭代器
- 目标区间与源区间不得重复
- 如果想让“两个源区间中都存在的元素”在目标区间中只出现一次,应使用set_union()
- 如果只想获得“同时存在于两个源区间内的”所有元素,应使用set_intersection()
下面的例子展示merge()的用法
#include"algostuff.h"
#include<iostream>
#include<iterator>
using namespace std;
int main()
{
list<int> col1;
set<int> col2;
INSERT_ELEMENTS(col1, 1, 6);
INSERT_ELEMENTS(col2, 3, 8);
PRINT_ELEMENTS(col1, "col1: ");
PRINT_ELEMENTS(col2, "col2: ");
cout << "merged: ";
merge(col1.begin(), col1.end(), col2.begin(), col2.end(), ostream_iterator<int>(cout, " "));
}运行结果如下
 (其中出现的第一个.h头文件在这里algostuff.h )
(其中出现的第一个.h头文件在这里algostuff.h )
注意在使用merge()算法的时候,对两个源区间内的元素顺序是有要求的,它们内部必须是已经排好序的,否则会出现程序错误
这里我们展示用两个没有内部排序的序列,再对其使用merge()算法后,会出现如下情况
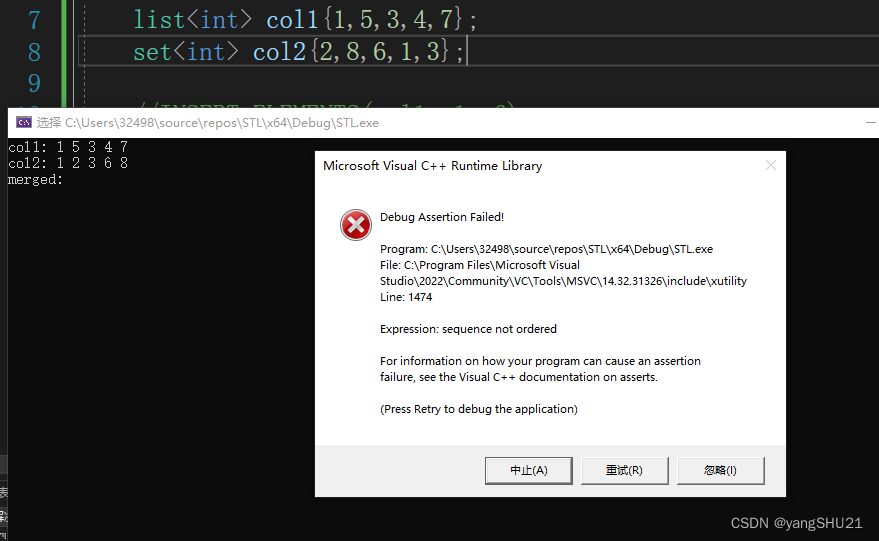
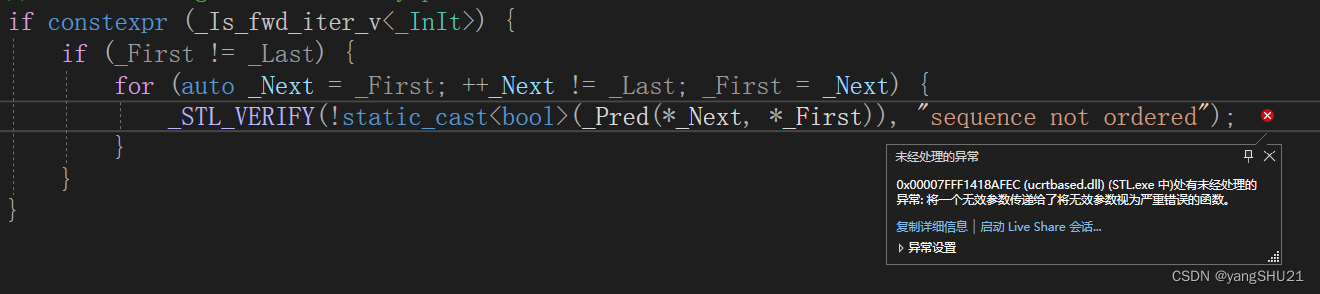
这里显示“sequence not ordered"
我们对两组数据进行修改,按照大小顺序拍好再进行merge()
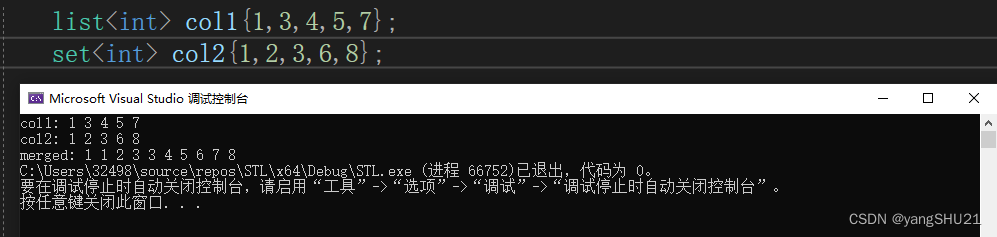
这个时候就可以得到正确的结果了。
两个已序集合的并集(union)
OutputIterator set_union(InputIterator source1Beg,InputIterator source1End,
InputIterator source2Beg,InputIterator source2End,
OutputIterator destBeg)
OutputIterator set_union(InputIterator source1Beg,InputIterator source1End,
InputIterator source2Beg,InputIterator source2End,
OutputIterator destBeg,BinaryPredicate op)- 将已序的源区间 [ source1Beg, source1End),[ source2Beg,source2End)内的元素合并,得到”以destBeg起始“的目标区间——这个区间内包含的元素要么来自第一个区间,要么来自第二个区间,或者是同时来自两个区间
- 目标区间内的所有元素都按顺序排列
- 同时出现于两个源区间内的元素,在目标区间中将只出现一次。但是假如原来的某个区间原本就存在重复元素,则目标区间也会有重复元素——重复的个数是两个源区间内的重复个数的较大值
如对1 2 2 4 6 7 7 9 和2 2 2 3 6 6 8 9这两个序列调用set_union()得到的结果是 1 2 2 2 3 4 6 7 7 8 9
- op是一个可有可无的操作,二元判断式,被当作排序准则
- 应确保两个源区间一开始就是已序的,同时还要保证目标区间够大,目标区间和源区间不得重叠
两个已序集合的交集(intersection)
OutputIterator set_intersection(InputIterator source1Beg,InputIterator source1End,
InputIterator source2Beg,InputIterator source2End,
OutputIterator destBeg)
OutputIterator set_intersection(InputIterator source1Beg,InputIterator source1End,
InputIterator source2Beg,InputIterator source2End,
OutputIterator destBeg,BinaryPredicate op)- 将已序的源区间 [ source1Beg, source1End),[ source2Beg,source2End)内的元素合并,得到”以destBeg起始“的目标区间——这个区间内包含的元素同时存在于两个区间。如对1 2 2 4 6 7 7 9 和2 2 2 3 6 6 8 9这两个序列调用set_intersection()得到的结果是2 2 6 9
- 目标区间的所有元素都是按顺序排列的
- 如果某个源区间内本来就存在有重复元素,则目标区间内也会有重复元素——重复的个数是两个源区间内重复个数的较小值
两个已序区间集合的差集(difference)
OutputIterator set_difference(InputIterator source1Beg,InputIterator source1End,
InputIterator source2Beg,InputIterator source2End,
OutputIterator destBeg)
OutputIterator set_difference(InputIterator source1Beg,InputIterator source1End,
InputIterator source2Beg,InputIterator source2End,
OutputIterator destBeg,BinaryPredicate op)- 将已序的源区间 [ source1Beg, source1End),[ source2Beg,source2End)内的元素合并,得到”以destBeg起始“的目标区间——这个区间内包含的元素只存在于第一源区间,不存在于第二源区间。如对1 2 2 4 6 7 7 9 和2 2 2 3 6 6 8 9这两个序列调用set_difference()得到的结果是1 4 7 7
- 目标区间的所有元素都是按顺序排列的
- 如果某个源区间内本来就存在有重复元素,则目标区间内也会有重复元素——重复的个数是第一源区间内的重复个数减去第二源区间内相应的重复个数,如果第二源区间内的重复个数大于第一源区间内的相应重复个数,目标区间内的对应重复个数将会是0
- 两者都返回目标区间内”最后一个合并元素“的下一位置
OutputIterator set_symmetric_difference(InputIterator source1Beg,InputIterator source1End,
InputIterator source2Beg,InputIterator source2End,
OutputIterator destBeg)
OutputIterator set_symmetric_difference(InputIterator source1Beg,InputIterator source1End,
InputIterator source2Beg,InputIterator source2End,
OutputIterator destBeg,BinaryPredicate op)- 将已序的源区间 [ source1Beg, source1End),[ source2Beg,source2End)内的元素合并,得到”以destBeg起始“的目标区间——这个区间内包含的元素或存在于第一源区间,或存在于第二源区间,但不同时存在于两源区间内。如对1 2 2 4 6 7 7 9 和2 2 2 3 6 6 8 9这两个序列调用该算法得到的结果是1 2 3 4 6 7 7 8
- 目标区间的所有元素都是按顺序排列的
- 如果某个源区间内本来就存在有重复元素,则目标区间内也会有重复元素——重复的个数是两个源区间内的对应重复元素的个数差额
- 两者都返回目标区间内”最后一个合并元素“的下一位置
下面我们展示上述提到的几种算法
#include"algostuff.h"
#include<iostream>
#include<iterator>
using namespace std;
int main()
{
int c1[] = { 1,2,2,4,6,7,7,9 };
int num1 = sizeof(c1) / sizeof(c1[0]);
int c2[] = { 2,2,2,3,6,6,8,9 };
int num2 = sizeof(c2) / sizeof(c2[0]);
cout << "c1: ";
copy(c1, c1 + num1, ostream_iterator<int>(cout, " "));
cout << endl;
cout << "c2: ";
for (auto c : c2)
{
cout << c << " ";
}
cout << endl;
//for_each(c2, c2 + num2, [](int a) {cout << a << " "; });
//merge
cout << "merge: ";
merge(c1, c1 + num1, c2, c2 + num2, ostream_iterator<int>(cout, " "));
cout << endl;
//set_union
cout << "set_union: ";
set_union(c1, c1 + num1, c2, c2 + num2, ostream_iterator<int>(cout, " "));
cout << endl;
//set_intersection
cout << "set_intersection: ";
set_intersection(c1, c1 + num1, c2, c2 + num2, ostream_iterator<int>(cout, " "));
cout << endl;
//set_difference
cout << "set_difference: ";
set_difference(c1, c1 + num1, c2, c2 + num2, ostream_iterator<int>(cout, " "));
cout << endl;
//set_symmetric_difference
cout << "set_symmetric_difference: ";
set_symmetric_difference(c1, c1 + num1, c2, c2 + num2, ostream_iterator<int>(cout, " "));
cout << endl;
}运行结果如下:
 这里我们再将这几种算法做以总结:
这里我们再将这几种算法做以总结:
merge()直接合并两个已序区间内的所有元素,最终得到的目标区间元素个数一定是两个源区间元素个数的和
set_union()算法是求两个已序区间的并集,对于重复元素的处理办法是,找两个区间内对应重复元素多的,比如例子中c1序列有两个元素”2“,c2序列有3个元素”2“,则最终目标序列就有3个”2“元素
set_intersection()算法是求两个已序区间的交集,最终得到的目标区间的元素,既是源区间1中的也是源区间2中的
set_difference()算法是求只存在于第一序列而不存在于第二序列中的元素,对于两个序列的重复元素,最终目标区间的个数=第一序列该元素个数-第二序列该元素个数,如果结果为负,则目标区间不存在该元素,(注意只能是第一序列-第二序列)
set_symmetric_difference()算法,目标区间的元素不能同时存在于两个区间中,只能是其中某一序列的元素
对于这几个算法我们可以结合数学中集合的相关概念进行学习

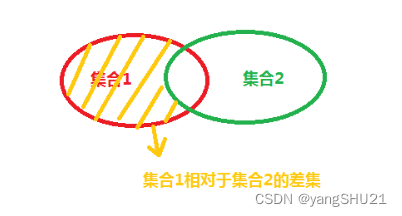
这样大家就会对这几个算法有深入的了解。





 文章介绍了C++中用于处理已排序区间元素的几个关键算法:merge()用于合并两个已排序区间,set_union()求并集,set_intersection()求交集,set_difference()求差集,以及set_symmetric_difference()求对称差集。每个算法都要求输入区间是有序的,并详细说明了它们的输出和处理重复元素的方式。
文章介绍了C++中用于处理已排序区间元素的几个关键算法:merge()用于合并两个已排序区间,set_union()求并集,set_intersection()求交集,set_difference()求差集,以及set_symmetric_difference()求对称差集。每个算法都要求输入区间是有序的,并详细说明了它们的输出和处理重复元素的方式。
















 4144
4144

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








