LDA_lda 分类数比维度多-优快云博客

关于降维算法
机器学习领域中所谓的降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : x->y，其中x是原始数据点的表达，目前最多使用向量表达形式。 y是数据点映射后的低维向量表达，通常y的维度小于x的维度（当然提高维度也是可以的）。f可能是显式的或隐式的、线性的或非线性的。
目前大部分降维算法处理向量表达的数据，也有一些降维算法处理高阶张量表达的数据。之所以使用降维后的数据表示是因为在原始的高维空间中，包含有冗余信息以及噪音信息，在实际应用例如图像识别中造成了误差，降低了准确率；而通过降维,我们希望减少冗余信息所造成的误差,提高识别（或其他应用）的精度。又或者希望通过降维算法来寻找数据内部的本质结构特征。

LDA与PCA都是常用的降维方法，二者的区别在于：

出发思想不同。PCA主要是从特征的协方差角度，去找到比较好的投影方式，即选择样本点投影具有最大方差的方向（在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。）；而LDA则更多的是考虑了分类标签信息，寻求投影后不同类别之间数据点距离更大化以及同一类别数据点距离最小化，即选择分类性能最好的方向。
学习模式不同。PCA属于无监督式学习，因此大多场景下只作为数据处理过程的一部分，需要与其他算法结合使用，例如将PCA与聚类、判别分析、回归分析等组合使用；LDA是一种监督式学习方法，本身除了可以降维外，还可以进行预测应用，因此既可以组合其他模型一起使用，也可以独立使用。
降维后可用维度数量不同。LDA降维后最多可生成C-1维子空间（分类标签数-1），因此LDA与原始维度N数量无关，只有数据标签分类数量有关；而PCA最多有n维度可用，即最大可以选择全部可用维度。

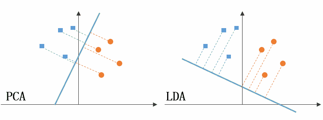
上图左侧是PCA的降维思想，它所作的只是将整组数据整体映射到最方便表示这组数据的坐标轴上，映射时没有利用任何数据内部的分类信息。因此，虽然PCA后的数据在表示上更加方便（降低了维数并能最大限度的保持原有信息），但在分类上也许会变得更加困难；上图右侧是LDA的降维思想，可以看到LDA充分利用了数据的分类信息，将两组数据映射到了另外一个坐标轴上，使得数据更易区分了（在低维上就可以区分，减少了运算量）。

接下来着重介绍LDA
LDA的全称是Linear Discriminant Analysis（线性判别分析），是一种supervised learning。有些资料上也称为是Fisher’s Linear Discriminant，因为它被Ronald Fisher发明自1936年，Discriminant这次词我个人的理解是，一个模型，不需要去通过概率的方法来训练、预测数据，比如说各种贝叶斯方法，就需要获取数据的先验、后验概率等等。LDA是在目前机器学习、数据挖掘领域经典且热门的一个算法，据我所知，百度的商务搜索部里面就用了不少这方面的算法。
LDA的原理是，将带上标签的数据（点），通过投影的方法，投影到维度更低的空间中，使得投影后的点，会形成按类别区分，一簇一簇的情况，相同类别的点，将会在投影后的空间中更接近。要说明白LDA，首先得弄明白线性分类器(Linear Classifier)：因为LDA是一种线性分类器。对于K-分类的一个分类问题，会有K个线性函数：
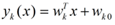
在这里插入图片描述
当满足条件：对于所有的j，都有Yk > Yj,的时候，我们就说x属于类别k。对于每一个分类，都有一个公式去算一个分值，在所有的公式得到的分值中，找一个最大的，就是所属的分类了。
上式实际上就是一种投影，是将一个高维的点投影到一条高维的直线上，LDA最求的目标是，给出一个标注了类别的数据集，投影到了一条直线之后，能够使得点尽量的按类别区分开，当k=2即二分类问题的时候，如下图所示：
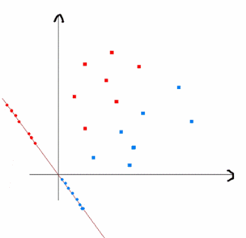
在这里插入图片描述
红色的方形的点为0类的原始点、蓝色的方形点为1类的原始点，经过原点的那条线就是投影的直线，从图上可以清楚的看到，红色的点和蓝色的点被原点明显的分开了，这个数据只是随便画的，如果在高维的情况下，看起来会更好一点。下面我来推导一下二分类LDA问题的公式：
假设用来区分二分类的直线（投影函数)为：
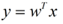
在这里插入图片描述
LDA分类的一个目标是使得不同类别之间的距离越远越好，同一类别之中的距离越近越好，所以我们需要定义几个关键的值。
类别i的原始中心点为：（Di表示属于类别i的点)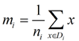
类别i投影后的中心点为：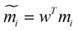

衡量类别i投影后，类别点之间的分散程度（方差）为：

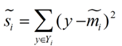
在这里插入图片描述
最终我们可以得到一个下面的公式，表示LDA投影到w后的损失函数：

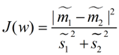
我们分类的目标是，使得类别内的点距离越近越好（集中），类别间的点越远越好。分母表示每一个类别内的方差之和，方差越大表示一个类别内的点越分散，分子为两个类别各自的中心点的距离的平方，我们最大化J(w)就可以求出最优的w了。想要求出最优的w，可以使用拉格朗日乘子法，但是现在我们得到的J(w)里面，w是不能被单独提出来的，我们就得想办法将w单独提出来。
我们定义一个投影前的各类别分散程度的矩阵，这个矩阵看起来有一点麻烦，其实意思是，如果某一个分类的输入点集Di里面的点距离这个分类的中心店mi越近，则Si里面元素的值就越小，如果分类的点都紧紧地围绕着mi，则Si里面的元素值越更接近0.
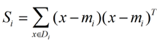
在这里插入图片描述
带入Si，将J(w)分母化为：

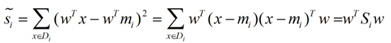
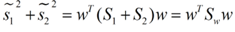
同样的将J(w)分子化为：
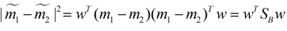
在这里插入图片描述
这样损失函数可以化成下面的形式：

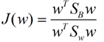
这样就可以用拉格朗日乘子法了，但是还有一个问题，如果分子、分母是都可以取任意值的，那就会使得有无穷解，我们将分母限制为长度为1（这是用拉格朗日乘子法一个很重要的技巧，在下面将说的PCA里面也会用到，如果忘记了，请复习一下高数），并作为拉格朗日乘子法的限制条件，带入得到：
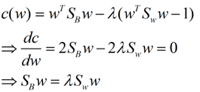
在这里插入图片描述
这样的式子就是一个求特征值的问题了。
对于N(N>2)分类的问题，我就直接写出下面的结论了：

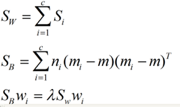
这同样是一个求特征值的问题，我们求出的第i大的特征向量，就是对应的Wi了。
这里顺便谈谈特征值，特征值在纯数学、量子力学、固体力学、计算机等等领域都有广泛的应用，特征值表示的是矩阵的性质，当我们取到矩阵的前N个最大的特征值的时候，我们可以说提取到的矩阵主要的成分（这个和之前的PCA相关，但是不是完全一样的概念）。在机器学习领域，不少的地方都要用到特征值的计算，比如说图像识别、pagerank、LDA、还有之前提到的PCA等等。

为了直观比较LDA与PCA的区别，我们这次实验还是使用iris数据集，数据集的背景知识在PCA的实验中已经提过，这里不再指出。

首先导入库
在这里插入图片描述
载入数据集

数据预处理
将数据集加载到pandas数据对象后，第一步是将数据集划分为特征和相应的标签，然后将结果数据集划分为训练集和测试集。以下代码将数据划分为标签和特征集：

上面的代码将特征集分配给X变量，而将第五列（标签）中的值分配给y变量。
以下代码将数据划分为训练集和测试集：
在这里插入图片描述
接下来为LDA执行特征缩放

然后就可以使用LDA了
只需要四行代码即可使用Scikit-Learn执行LDA。 sklearn.discriminant_analysis库的LinearDiscriminantAnalysis类用于执行LDA。

在上面的代码中，LinearDiscriminantAnalysis类作为LDA导入。与PCA一样，我们必须传递LDA的n_components参数的值，该参数指的是我们需要的线性判别的数量。我们将n_components设置为1，因为我们首先要使用单个线性判别式来检查分类器的性能。然后执行fit和transform。

注意，在LDA的情况下，transform方法有两个参数：X_train和y_train。然而，在PCA的情况下，transform方法仅需要一个参数，即X_train。这说明LDA在选择线性判别式时考虑输出类标签，而PCA不依赖于输出标签。

由于我们想要将带有一个线性判别式的LDA的性能与具有一个主成分的PCA的性能进行比较，所以我们使用与用于评估PCA的性能相同的随机森林分类器。
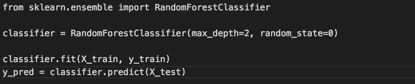
在这里插入图片描述
最后一步是在通过混淆矩阵评估算法的性能，并计算预测的准确率

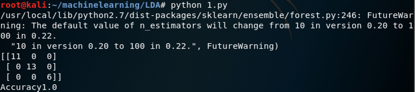
可以看到，使用一个线性判别式，算法实现了100％的精度，这大于PCA一个主成分所达到的精度，即93.33％。
那么我们以后就一定使用LDA吗?就不需要PCA了吗？
我们应该明白这两个算法的原理是不一样的，pca是选择投影后使得数据方差最大的方向来投影，假设就是方差越大，信息量越多，pca是一种无监督算法，没有类别信息，而lda是选择投影后使得类内方差小而类间方差大的方向来投影，用到了类别信息，所以选择用哪种算法来降维应该是根据具体的目的和场景来的，如果你的目的就是分类，那么显然lda的选择标准更合理，如果没有类别信息（无监督），那就只能选pca，总之，两者选择投影的方向的标准是不一样的，看哪个和我们的需要更契合

参考：
1．《机器学习》（西瓜书）
2. https://www.zhihu.com/question/35666712
3. https://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html
4. https://cloud.tencent.com/developer/article/1106120
5. https://stackabuse.com/