每日一题

最新推荐文章于 2023-03-07 18:22:05 发布

原创最新推荐文章于 2023-03-07 18:22:05 发布 · 310 阅读

CC 4.0 BY-SA版权

技术人除了焦虑，你还要每日一题。每日会持续更新...

一、题目：

var arr = [1, 2, 3];
arr[10] = 10;
var  filtered = arr.filter((x) => x === undefined)
console.log(filtered);
arr.map(x => console.log(x))
console.log(arr)

答案（Chrome输出）

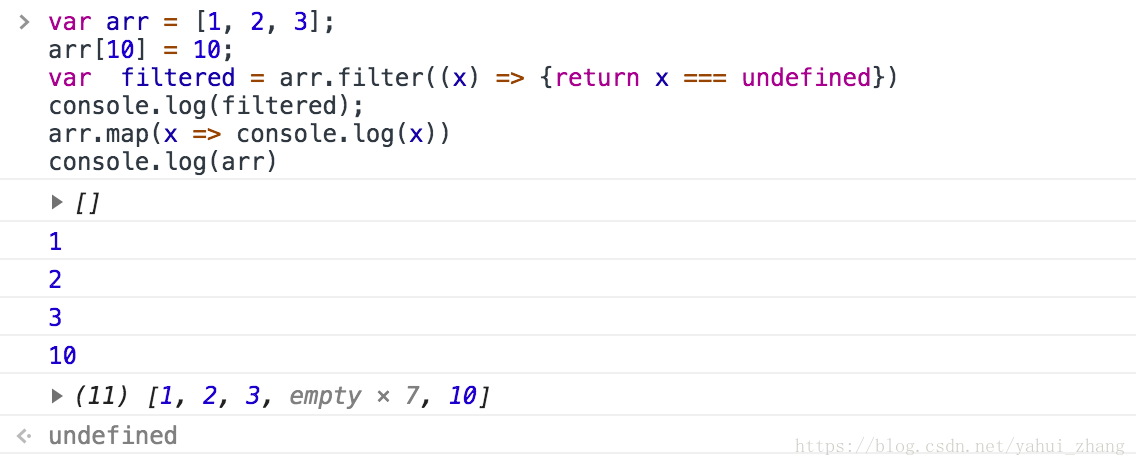
知识点：js对于数组中被跳过的位置放的是empty items，不是undefined, empty items遍历的时候会被跳过；

二、题目

async function async1(){
  console.log('async1 start')
  await async2()
  console.log('async1 end')
}
async function async2(){
  console.log('async2')
}
console.log('script start')
setTimeout(function(){
  console.log('setTimeout') 
},0)  
async1();
new Promise(function(resolve){
  console.log('promise1')
  resolve();
}).then(function(){
  console.log('promise2')
})
console.log('script end')

答案（Chrome输出）

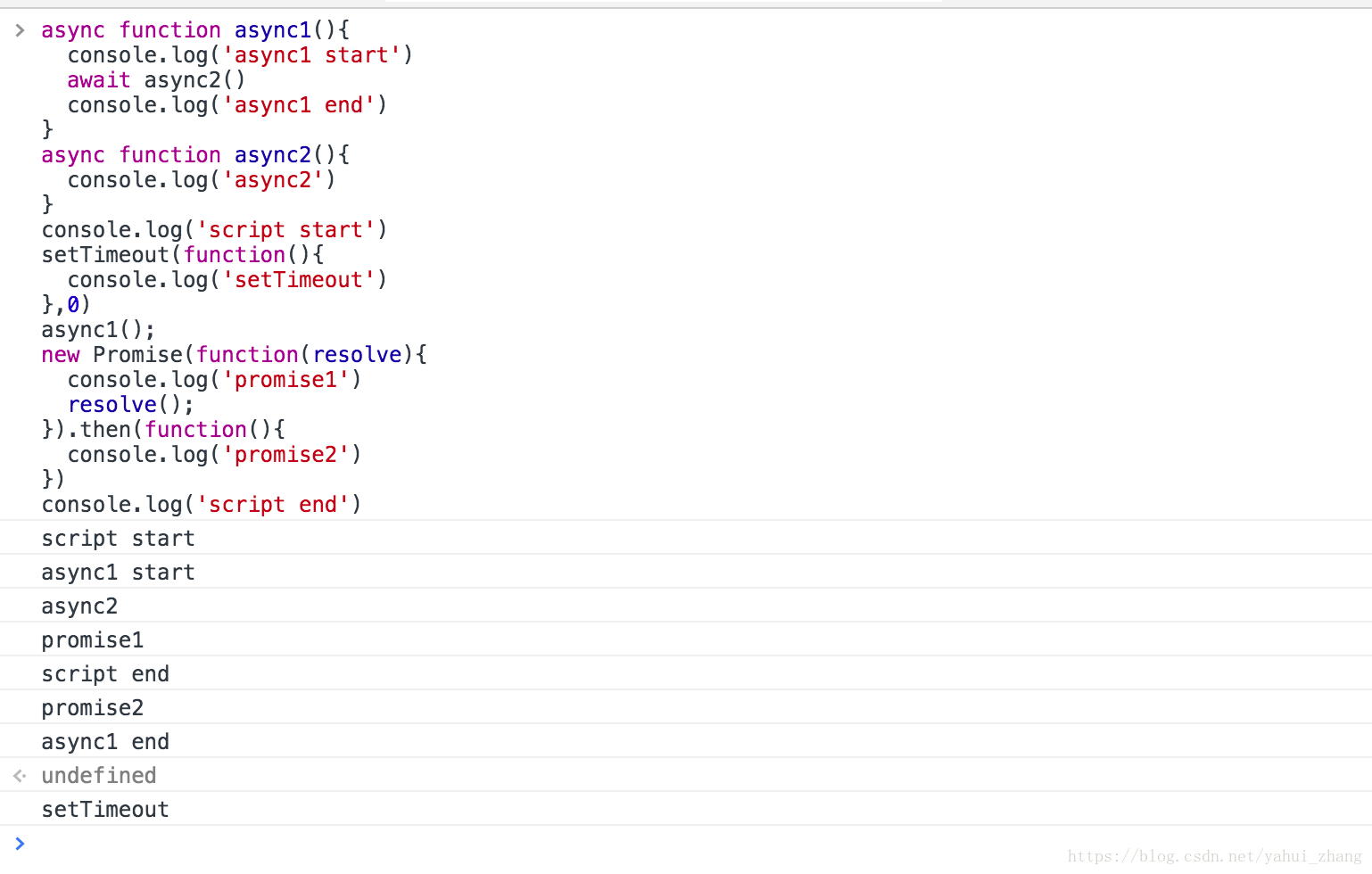
知识点：

js是单线程的。
promise被定义后是立即执行的，但它返回的resolve是异步的。
promise的异步优先级高于setTimeout（这个如果不懂可以看下js的Event loop和task queue）
async会返回一个promise对象，await关键字会让出线程。

下面分析下代码执行流程：
1、执行console.log('script start')，输出script start；
2、执行setTimeout，是一个异步动作，放入异步队列中；
3、执行async1()，输出async1 start，继续向下执行；
4、执行async2()，输出async2，并返回了一个promise对象，await让出了线程，把返回的promise加入了异步队列，所以async1()下面的代码也要等待上面完成后继续执行;
5、执行 new Promise，输出promise1，然后将resolve放入异步队列；
6、执行console.log('script end')，输出script end；
7、到此同步的代码就都执行完成了，然后去异步队列里去获取任务，现在队列中有一个promise（async2返回的），resolve（new Promise的），和setTimeout，先取出promise执行，默认返回resolve，再次加入了异步队列，现在就队列就变成了resolve（new Promise的），resolve（async2返回的promise返回的），setTimeout。
8、然后执行resolve（new Promise的），输出了promise2。
9、接下来执行resolve（async2返回的promise返回的），输出了async1 end。
10、最后执行setTimeout，输出了settimeout。
以上是我个人理解，如有错误欢迎指正；