快速排序

快速排序是一种最坏情况时间复杂度为Θ($n^2$)的排序算法，其最坏情况的时间复杂度很差，但是快速排序通常是实际排序应用中最好的选择，在面试过程中也会经常被提到，它的平均性能非常好。它的期望时间复杂度为Θ($nlogn$)，而且Θ($nlogn$)中隐含的常数因子非常小；另外，它还能进行原址排序（In-place sort ：在排序算法中。如果输入数组中仅有常数个元素需要在排序过程中存储在数组之外，则称排序算法是原址排序）
快速排序也用到了分治的思想，首先，它将待排序数组 A[p….r] 划分为两个子数组：A[p….q-1]和 A[q+1….r]，前者所有元素小于等于 A[q] ,后者所有元素大于等于 A[q] ；其次通过递归调用快速排序过程，对上面两个子数组进行排序；最后，由于数组使用原址排序，不需要合并，数组 A[p….r] 就已经排好序了。
下面是快速排序的伪代码，A为待排序数组，p为A的起始位置，从1开始，r为A的终止位置，r = A.length ：

QuickSort(A,p,r)
    if p < r:
        q = Partition(A,p,r)
        QuickSort(A,p,q-1)
        QuickSort(A,q+1,r)

Partition(A,p,r)
    x = A[r]
    i = p-1
    for j = p to r-1
        if A[j] <= x
            i = i+1
            exchange A[i] with A[j]
    exchange A[i+1] with A[r]
    return i+1

算法解释：
快速排序的思想就是选择数组中最后一个元素(这个可随机选取)，用这个元素对待排序数组进行划分，这个元素的左边都是小于等于这个元素的，右边都是大于等于这个元素的。
上述的伪代码过程包含了两个指针，一个是 i ，一个是 j ；算法首先选取A数组最后一个元素，假设为元素a，然后遍历整个排除a元素的数组，在 i 指针左边的元素(包括 i 指针)都是小于等于所选a元素的，在 i+1 指针到 j 指针之间的元素都是大于等于所选a元素的，j 指针指向的是待比较的元素，j 指针右侧是未做比较的元素。当 j 所指的元素小于a元素时，i 加一，让 i+1 指向元素与 j 指向元素互换，这样就将小于a元素的元素包含在 i 及 i 的左侧元素中；若 j 所指元素大于a元素时，j 加一，即将这个元素包含在 i 和 j 指针之间，当 j 达到A.length - 1时，比较停止。这个时候将a元素和 i + 1 元素做对调，对调之后 i+1 位置为a元素，其左侧是小于等于a的元素集合，右侧是大于等于a的元素集合，一轮比较结束。

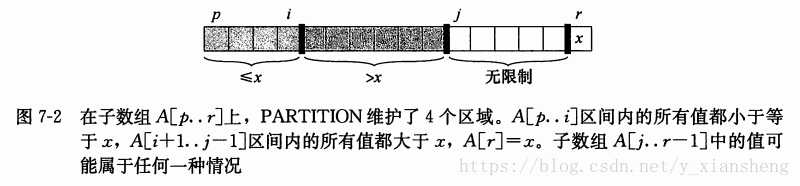
上述过程结束后，将数组从a元素处切割成两个数组，小于等于a的集合和大于等于a的集合，然后利用递归，对这两个数组再进行上述的排序，直到不满足递归条件，即 p < r，排序结束。
快速排序的过程可结合下图进行学习。

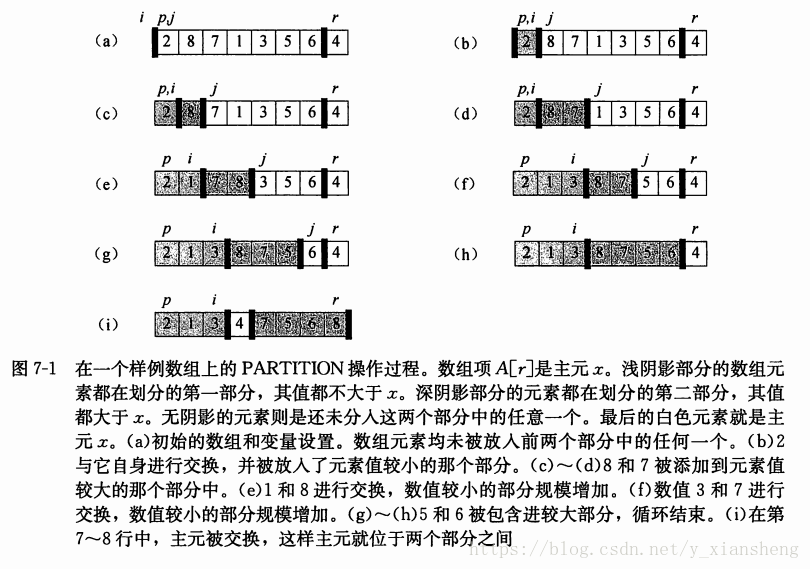
参考文献： 算法导论第三版