| 如何证明Coq标准库中filter引理 |
|---|
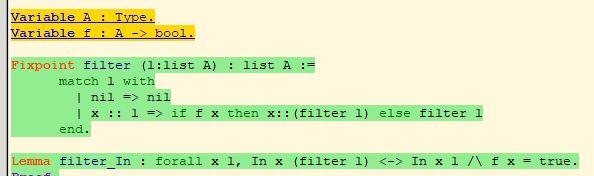
| Require Import Arith. Require Import ZArith. Require Import Bool. Require Import List. Variable A : Type. Variable f: A -> bool. Fixpoint filter (l:list A) : list A := \quad match l with \quad | nil => nil \quad | x ::l => if f x then x :: (filter l) \qquad \qquad else filter l \quad end. Lemma or_and : forall P Q R : Prop, (P / Q) /\ R <-> (P /\ R) / (Q /\ R). Proof . \quad unfold iff. \quad intros P Q R. \quad split. \quad - intros [[H | H0] H1]. \qquad + left. \qquad \quad Search and. \qquad \quad apply conj. \qquad \quad * apply H. \qquad \quad * apply H1. \qquad + right. \qquad \quad apply conj. \qquad \quad * apply H0. \qquad \quad * apply H1. \quad - intros [[H H0] | [H1 H2]]. \qquad + apply conj. \qquad \quad * left. \qquad \qquad apply H. \qquad \quad * apply H0. \qquad + apply conj. \qquad \quad * right. \qquad \qquad apply H1. \qquad \quad * apply H2. Qed . Lemma filter_in : forall x l, In x (filter l) <-> In x l /\ f x = true. Proof . \quad intros x l. \quad generalize dependent x. \quad induction l as [| n l’ IHl’]. \quad - intro x. \qquad split. \qquad + intro H0. \qquad \quad simpl in H0. \qquad \quad inversion H0. \qquad + intros [H0 H1]. \qquad \quad simpl. \qquad \quad inversion H0. \quad - intro x. \qquad split. \qquad + simpl. \qquad \quad intro H0. \qquad \quad destruct (f n) eqn : H. \qquad \quad * rewrite -> or_and. \qquad \qquad simpl in H0. \qquad \qquad destruct H0. \qquad \qquad { left. \qquad \qquad \quad rewrite H0 in H. \qquad \qquad \quad apply conj. \qquad \qquad \quad apply H0. \qquad \qquad \quad apply H. \qquad \qquad } \qquad \qquad { right. \qquad \qquad \quad apply IHl’. \qquad \qquad \quad apply H0. \qquad \qquad } \qquad \quad * rewrite -> or_and. \qquad \qquad right. \qquad \qquad apply IHl’. \qquad \qquad apply H0. \qquad + simpl. \qquad \quad intros [[H | H0] H1]. \qquad \quad * destruct (f n) eqn : H2. \qquad \qquad { simpl. \qquad \qquad \quad left. \qquad \qquad \quad apply H. \qquad \qquad } \qquad \qquad { rewrite H in H2. \qquad \qquad \quad rewrite H1 in H2. \qquad \qquad \quad inversion H2. \qquad \qquad } \qquad \quad * destruct (f n) eqn : H2. \qquad \qquad { simpl. \qquad \qquad \quad right. \qquad \qquad \quad apply IHl’. \qquad \qquad \quad apply conj. \qquad \qquad \quad apply H0. \qquad \qquad \quad apply H1. \qquad \qquad } \qquad \qquad { apply IHl’. \qquad \qquad \quad apply conj. \qquad \qquad \quad apply H0. \qquad \qquad \quad apply H1. \qquad \qquad } Qed . |

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








