带写入驱动器的RRAM架构

带写入驱动器的阻变式RAM架构

1. 引言

在过去35年中，基于MOS晶体管中电荷俘获的闪存发展迅速，甚至超越了摩尔定律。当尺寸缩小至20 nm以下时，面临诸多挑战，主要是误码率上升和写入耐久性下降；而当尺寸低于15 nm时，这些挑战变得难以承受[1]。近年来，为了寻找比闪存更理想的替代技术，人们开发了多种新技术，这些技术具备非易失性、高密度、较高的写入耐久性、在15 nm以下具有良好的可扩展性、快速读写等共同特性，其中一些技术还具备足够高的速度和耐久性，可作为SRAM和DRAM的替代方案，从而实现通用存储器的应用[2]。RRAM具备高开关速度[7], 、低功耗以及高封装密度[8]等多种优势，因此被视为硅基闪存的替代选择[9]。此外，由于RRAM与CMOS[10], CNFET[11],兼容且具有高度可扩展性[9], ，在纳米尺度下有望超越传统高性能内存（如传统SRAM）的性能。因此，RRAM被认为是内存应用领域最有前景的技术[12, 13]。这些特性使得忆阻器被广泛应用于非易失性内存设计[3], 、神经形态系统[4], 、可编程逻辑[5], 、非线性电路[6],以及模拟和数字电路[7]等多个领域。

1971年，莱昂·楚阿基于对四个基本变量——电压 (V)、电流 (I)——之间关系的六种可能组合的对称性考虑，提出了缺失的电路元件（除电阻、电容器和电感 [8]  之外）存在的理由，磁通量（ϕ），以及电荷（q）。电荷和磁通量分别是电流和电压对时间的积分。电阻通过欧姆定律将电压与电流关联（V =  IR），电容器通过（q =  CV）将电荷与电压关联，电感器通过（ϕ=  LI）将电流与磁通量关联。由于存在第六种关系的可能性，蔡提出了一个能够关联电荷与磁通量的第四种基本电路元件，并将该器件命名为忆阻器（memristor），即“记忆电阻”。基于忆阻器的存储器可实现100 Gbits/cm²的集成密度，因为可以利用现有的CMOS制造技术进行三维集成。此外，其在CMOS逻辑模块上方的交叉阵列架构可能使其比3D NAND闪存技术更加密集。

在光照下 ，上述 ove讨论本文论文做出以下贡献 ions:

(1) 第2节对两种忆阻器模型进行了详细研究。(2) 第3节清楚地解释了忆阻器的工作原理。(3) 第4节说明了使用写驱动器的提出的读写电路。(4) 第5节解释了8 × 8 RRAM的提出架构及其工作原理。(5) 第6节包含基于PVT变化的提出电路的稳定性分析。(6) 第7节给出了仿真结果以及提出的存储器与其他存储器（基于NAND和NOR的闪存、双极性存储器和MCAM）的比较。

2. 忆阻器模型

与其它两端电路元件（即电阻、电容器和电感）相关，蔡提出忆阻器作为磁通量与电荷之间的缺失环节，即 M dq= dϕ ，其中‘M’为忆阻值。

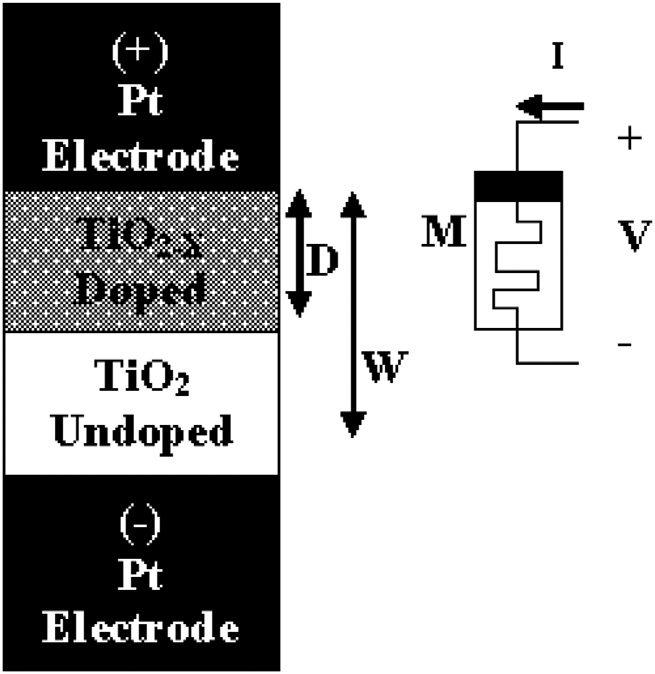
斯特鲁科夫等人 [10]提出了忆阻器的物理模型，该模型由夹在两个金属触点之间的薄半导体薄膜（可电切换）构成。该半导体薄膜长度为 D，由两层不同的二氧化钛薄膜组成。其中一层是纯 TiO₂（未掺杂层），具有高电阻率；另一层是富含氧空位的高导电掺杂层。状态变量‘W’表示掺杂区（TiO₂₋ₓ层）的宽度。当在忆阻器两端施加外加电压时，电场排斥掺杂层中带正电的氧空位，导致长度发生变化，从而改变忆阻值，即忆阻器总电阻。当掺杂区完全扩展（即 D/W = 1）时，忆阻值记为 R ON；当未掺杂区完全扩展（即 D/W = 0）时，则记为 R OFF。氧空位在未再次施加电压前保持不移动，从而使忆阻器具有非易失性。

2.1. 理想忆阻器模型 for ideal memristor

在 a电流‐受控忆阻器[9],的忆阻值 R仅取决于电荷 ，并可表示为 ,

$$ V_m = R(q(t)) \times I $$ (1)

虽然电荷与电流的关系为 I= dq/dt。通常，一种流行的模型[10]基于以下考虑：忆阻型器件由两个不同的区域组成（一个是低阻态，另一个是高阻态），其间具有变化的边界。

忆阻器的总忆阻值可以表示为低电阻状态和高电平电阻状态的电阻之和，如下所示

$$ R(x) = R_{on}(x) + R_{off}(1 - x) $$ (2)

此处， $x \in [0,1]$给出从一端起的边界位置，而 $R_{ON}$ （低电平电阻状态下的电阻）和 $R_{OFF}$ （高电平电阻状态下的电阻）是忆阻值的边界值。

运动的方程可以使用窗函数W(x)来表示

$$ \frac{dx}{dt} = k \times W(x) \times I(t) $$ (3)

其中，k = u V R on D2  是仅依赖于忆阻器参数的常数，如 [11], μv ≈ 10⁻¹⁴ m² s⁻¹ V⁻¹  所述，即所谓的掺杂剂迁移率，W(x) 是通常选为 [12] 的窗函数

$$ W(x) = 1 - (2x - 1)^{2p} $$ (4)

其中W(x)由参数p控制。本文考虑了各种忆阻器模型[17–24] ，并在本研究的仿真中采用了[24]的最先进的忆阻器模型。若干研究小组提出的忆阻器模型[18, 19]存在一些问题，因为这些模型会陷入端态，且缺乏可扩展性。尽管[17],的模型具有一定的可扩展性，但其边界处的不连续性使该模型变得脆弱。另一方面，在[20]中采用反馈实现后，端态问题得到了解决。如所见，本研究采用了[24]的最先进的忆阻器模型作为基于物理与本征状态变量的模型，该模型采用非线性变换函数来克服上述问题，而不是使用窗函数。

此处 p 是一个正整数，用于描述开关线性度；通常，具有较高开关线性度的物理器件其 p 值也较大。特性：窗函数 w(x) 取忆阻值的边界值。该函数没有开关阈值，对忆阻器中的波动不稳定，并表现出更高的延迟开关 [13] 。公式 (2)–(4) 描述了一个理想的电流控制型忆阻器。一般情况下，对于任意函数 W(x)，可对 (3) 进行积分，从而将“x”表示为电荷量 q 的函数。例如，如果 W(x) 由 (4) 给出且 p = 1，则可得到如 (5) 所示的关系。

$$ \frac{1}{4} \ln \left( \frac{x}{1 - x} \right) = k [q(t) + q(0)] $$ (5)

其中 电荷量 q(0) 是 the 积分 常数 （初始 条件）。 因此 entl y

$$ R(q(t)) = R_{off} + \frac{R_{on} - R_{off}}{e^{-4k[q(t) + q(0)]} + 1} $$ (6)

它可以更方便地用初始忆阻值和初始 memristance $R_{initial}=R(q(0)$来重写，从而得到

$$ R(q(t)) = R_{off} + \frac{R_{on} - R_{off}}{a e^{-4k \times q(t)} + 1} $$ (7)

其中，

$$ a = \frac{R_{initial} - R_{on}}{R_{off} - R_{initial}} $$ (8)

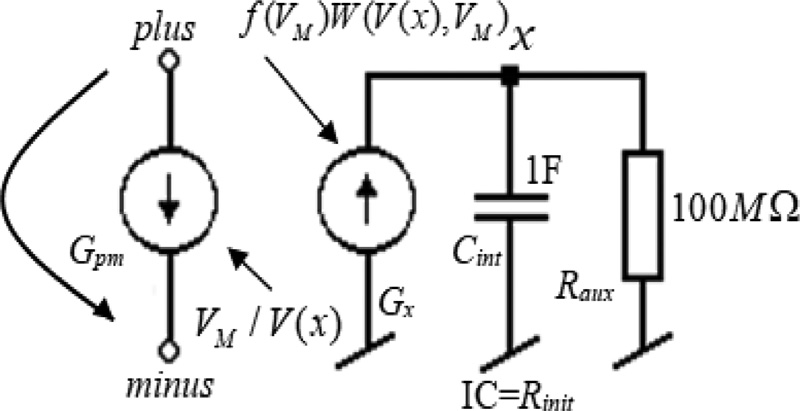
公式 (7) 表示适用于 SPICE仿真 的模型：忆阻值被表示为状态变量 q 的函数，因此与 (3) 相比，该状态方程对截断误差不敏感。在 SPICE 中，电荷可以通过积分电容 C_int 对端口电流 I 进行积分得到，如 图 2 所示。然后，以库仑为单位的电荷等于节点 Q 以伏特为单位的电压。从 公式 (7) 可以明显看出，忆阻元件可以被建模为一个固定的 R OFF 电阻和一个受控电压源的串联连接（见 图 2）。

第二节‐IIA 中解释的简单模型考虑了忆阻器的边界电阻值。该模型未考虑开关阈值，对参数变化不具有免疫性，并且表现出更长的开关延迟 [13, 25] 。尽管该模型本质上很简单，但它存在一个固有的问题。当两端施加较大的电场时，它无法捕捉到非线性效应 [13, 25] 。

2.2. 具有阈值的双极性忆阻器模型

文献中提出了多种方法，用于处理阈值电压型开关 [14–18] 。由于实际的忆阻型器件是因器件两端电场变化而发生开关（而非因其流过电流的变化），并由此引发原子迁移，导致忆阻器电阻发生变化。因此，电压控制模型 [14, 16, 18] 比电流控制模型 [17, 15]  更加符合实际情况。本研究采用文献 [14, 16, 18]  中提出的电压控制模型。在该模型中，忆阻值 R 充当内部状态变量 x，即 x≡ R，该变量通过以下方程定义器件的状态

$$ I = x^{-1} V_M $$ (9)

$$ \frac{dx}{dt} = f(V_M) W(x, V_M) $$ (10)

其中 f(.)是一个函数 ，用以建模器件的阈值特性 （参见 Fig. 3 ） ，而W(.) 是 窗函数：

$$ f(V_M) = \beta(V_M - 0.5[ |V_M + V_t| - |V_M - V_t| ]) $$ (11)

$$ W(x, V_M) = \theta(V_M) \theta(R_{off} - x) + \theta(-V_M) \theta(x - R_{on}) $$ (12)

这里 θ(• ) 是阶跃函数，β  是一个正的常数，用于表征当 |V M| > V t 时忆阻值变化速率，V t 是（正或负的）阈值电压，R ON 和 R OFF 是忆阻值 R 的限幅值。在 (12) 中，θ‐函数的作用是确保忆阻值的变化保持在 R ON 和 R OFF 的区间内。

近年来已研究了多种金属氧化物基忆阻器器件，每种器件根据所用材料的不同具有独特的R_ON / R_OFF 比值和开关阈值[18] 。此外，随着器件尺寸的减小，忆阻器件的V t显著降低。因此，遵循当前趋势，我们选择了100 Ω /10k Ω的R_ON / R_OFF 比值和0.2 V的阈值电压。所使用的模型参数如表1所示。

参数	值描述
R_ON(欧姆)	100最小电阻
R_OFF(欧姆)	10K最大电阻
Vt (volts)	0.2电阻变化阈值
β	10¹³忆阻值变化率

公式 (9)–(12) 对双极性忆阻器进行了紧凑且真实的描述。该模型考虑了忆阻值的边界值以及具有阈值特性的开关自然。在大多数实际的忆阻器中，电阻的变化是由于外加电场引起的原子迁移，而不是由电流流动导致的。因此，具有电压阈值 [14][16],  的模型在物理上优于具有电流阈值 [15, 17]的模型。

在此模型中，忆阻值的导数（10）由受控源 G x 的电流建模，其积分即为以欧姆为单位的忆阻值，等于节点x的电压（见图4）。根据公式（9），忆阻端口通过电流源 G pm 建模，其电流计算为端电压与忆阻值之比。方程（11）和（12）包含不连续函数（阶跃函数）以及具有不连续导数的函数（绝对值项），这些可能引发严重的收敛问题，特别是在使用大规模模型的应用中。在这种情况下，可采用基于S型函数对阶跃函数进行平滑建模的平滑函数，其公式如下所示

$$ \theta_s(x) = \frac{1}{1 + e^{-x/b}} $$ (13)

其中 b是一个平滑参数。然后，绝对值函数 abs S ( x ) 的平滑版本可以 e

$$ abs_S(x) = x[\theta_S(x) - \theta_S(-x)] $$ (14)

如果出现收敛问题，通常可以通过改进和微调b参数，在精度与可靠性之间找到适当的折中方案。为简便起见，相应的平滑函数stp S(x)、abs S(x)以及由它们导出的函数f S(x)和W S(x)直接在各个子电路的HSPICE代码中定义。

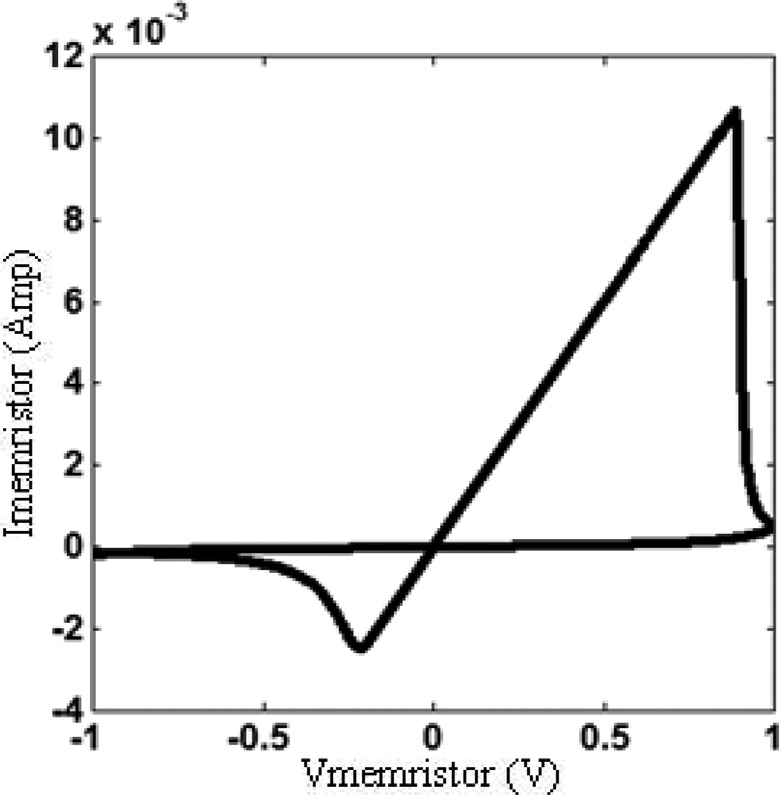
结果：如图3所示，当忆阻型器件受到幅值为Vmax > V_tp的正弦波电压V_M激励时，函数f(V_M)会产生窄脉冲。考虑图5中的正脉冲，它将被积分到节点x的电压中，直到忆阻值R = V(x)接近其边界值R_ON。此时，窗函数W以及源G_x的电流被设为零，忆阻值被固定在R_OFF。该状态将持续到电压V_M下降至负阈值电平V_tn以下。随后，函数f(V_M)变为负，导致源G_x产生负电流脉冲，其积分将使忆阻值向R_OFF减小。显然，尽管忆阻值尚未降至下限，但在电压V_M超过阈值V_t（无论是正还是负）的瞬间，电流被切断，即窗函数W的作用。当电压V_M在两个阈值电平之间的稳定区内变化时，忆阻值始终保持在低电平。此后系统在其周期稳态范围内继续运行。

3. 忆阻器工作原理

忆阻器模型可以如[3]中所述，采用忆阻器作为压控电流源或流控电压源来建立。我们在工作中使用的模型是压控电流源型。因此，流经G x的电流取决于施加在忆阻器两端的电势差，该电势差会改变电容器(C_x)中存储的电荷，因为其非零，且由于V (x) = q / C(x) = R mem使得忆阻值依赖于其电压差，从而证明了该模型名称的合理性。

因此，在单元中写入时，应改变电容器中存储的电荷，以覆盖先前存储的数据。写入的是零还是取决于忆阻器两端电势差的符号。当V(负极) ‐ V(正极) > |V t| 时，通过Gx的电流将非零且正，导致Cx放电。此过程将持续，直到V(x)降至最小值R_ON，之后由θ S(x)将其置为零，从而实现成功写操作。当V(负极) ‐ V(正极) ≤ |V t| 时，G_x将给电容器充电，直到V(x)达到最大值R_OFF，类似地完成写操作。

然而，在读取的情况下，由于我们不想覆盖数据，G x 的值应为零。这可以通过两种方式实现， either by making f S ( x ) zero or θS ( x ) zero。这样可以防止数据损坏，并成功进行读操作。

忆阻器的特性I‐V曲线（见图5）描述了由于其电阻变化，流经忆阻器的电流随其两端电源电压的变化情况。当忆阻器两端施加的电压在正方向增加（超过正阈值电压V tp）时（见图1和图3），掺杂层的宽度增大，使器件进入导通状态，从而导致电流迅速增加。然而，当在忆阻器两端施加负方向的电压（低于负阈值电压V tn）时，掺杂层的宽度减小，使器件进入关断状态，导致电流迅速减小并反向流动。如果所施加的电压介于V tp和V tn之间，则器件保持在相同的电阻状态。该曲线的非对称性是由于R ON与R OFF的值差异较大所致，这种差异提高了系统的鲁棒性，因为若要引起数据损坏，需要有大量电流在相反方向上流动。忆阻器的特性曲线，即捏滞回线，表明当其两端电压为零时，电流也为零。

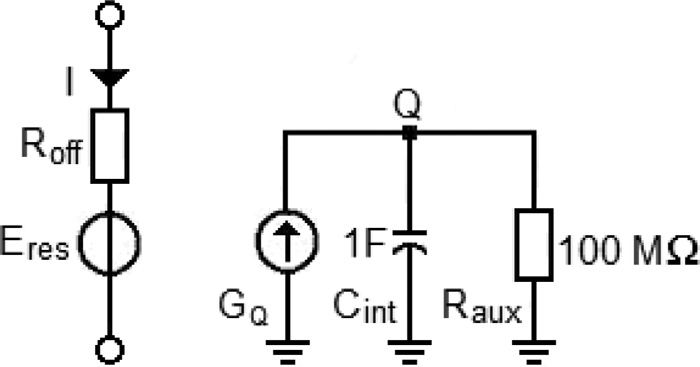
图5中的I‐V特性曲线以忆阻器两端的电压（x轴）和流过忆阻器的电流（y轴）绘制，两个值均通过双极性阈值模型（在第II‐B节中解释）获得。

从图5可以看出，在V tp（正向阈值）和V tn（负向阈值）之间没有电阻变化。

4. 使用写入驱动器的读取和写入电路

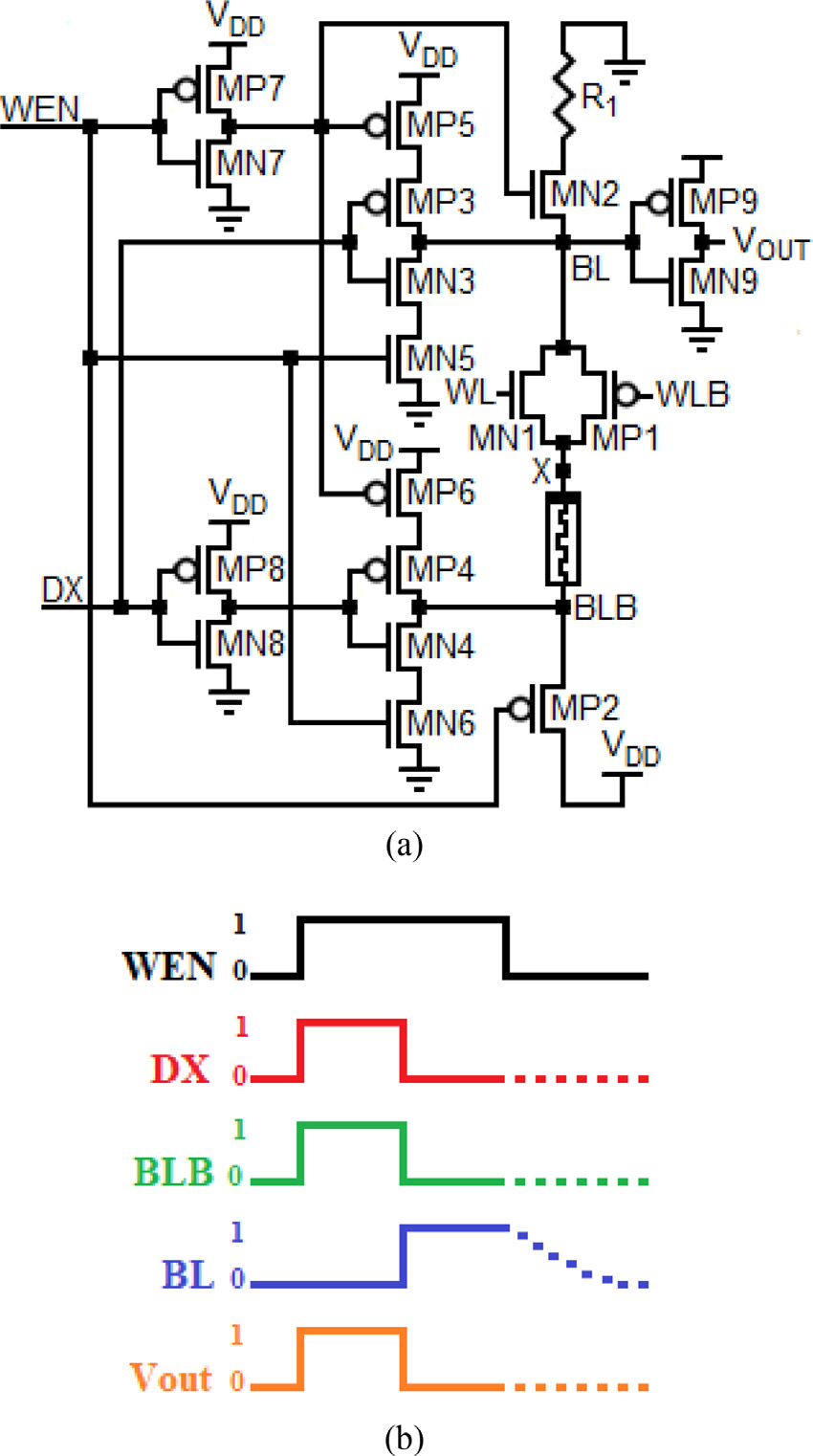
在图6(a)所示的提出的电路中，忆阻器与传输晶体管构成RRAM单元。晶体管MP1和MN1为访问晶体管（因此由WL和WLB控制信号控制）。这些晶体管根据当前操作为读写电路提供对忆阻元件的信息存储/读取访问。同时，在保持操作期间，它们阻止对该忆阻元件的访问，从而防止数据损坏。图6(b)展示了当提出的电路被激励时每个变量的波形。

使用写驱动器的读写电路以及 (b) 电路激励时每个变量的波形)

提出的电路包括写驱动器，该写驱动器由MN3、MN4、MN5、MN6、MN8、MP3、MP4、MP5、MP6和MP8组成。MN7和MP7未包含在写驱动器模块中，因为该反相器的输出需要被读取电路中的MN2访问，以在读操作期间导通，并在写操作期间保持关断状态。除MN7、MN8、MP7和MP8外，其余所有晶体管的尺寸均为400 × W/L（其中W/L为= 32 nm/32 nm）。W和L分别表示晶体管的沟道宽度和沟道长度。较大的尺寸要求是由于流经忆阻器所需的电流较大。较大的电流会增加或减小掺杂区的宽度，从而使忆阻值达到R ON / R OFF状态。而MP8和MN8、MP7和MN7的尺寸为W/L = 32 nm/32 nm，因为它们的作用不是驱动忆阻元件，而是实现导通与关断状态之间的切换。晶体管使其尺寸变得不重要。写驱动器确保当写使能(WEN)为高电平时，BL和BLB分别被驱动为DX和DXB的互补状态，其中DX表示要写入RRAM单元的数据。当使能为低电平时，MN3、MN4、MP3和MP4的源极将悬空，从而使BL和BLB悬空，进而将写驱动器与其余电路隔离。合理设置MN3、MN4、MN5、MN6、MN7、MN8、MP3、MP4、MP5、MP6、MP7和MP8的尺寸可确保在写操作期间忆阻器两端电压的幅值大于开关阈值电压。

例如，如果需要向RRAM单元中写入数据= 1 ，则WEN为一，因为这是一个写操作，且DX为一，因为DX代表数据。这导致忆阻器两端电压大于零（且高于|V t|），从而使忆阻值从初始状态变为R OFF。类似地，如果需要写入数据= 0 ，则WEN为一，DX为零，使BL驱动至V DD，BLB驱动至地。这导致忆阻器两端电压小于零（且低于‐|V t|），从而使忆阻值从R OFF变为R ON。

读取电路由晶体管MP9、MN9、MN2和MP2组成。MN2和MP2负责在忆阻器两端产生负电位差。在读操作期间，WEN接地，MP2导通，通过MP2的源极将V DD连接到BLB。这导致电流从V DD经MP2、忆阻器、TG（即MN1||MP1）、MN2和R1流向地。在读操作期间，我们必须注意两件事

(a) 数据必须不被覆盖且 (b) 存储的数据应该反映在输出行中。

为了了解如何确保第一件事，我们将分别查看read1和read0周期。在read1期间，由于忆阻值已处于R OFF状态，由于θ S (x)函数的作用，通过G x的电流变为零，从而防止了数据被覆盖。而在read 0中，忆阻值处于R ON状态，但路径中的电阻和晶体管的尺寸设计使得忆阻器两端电压不超过|V t| ，导致G x为零，因此此处也不会发生数据覆写。

现在，为了确认第二点如何实现，我们将关注节点X电压，因为该节点的电压取决于忆阻器中写入的数据（即忆阻值）。因此，我们应当测量节点X以了解存储单元中写入的数据（或忆阻值）。但由于无法直接访问忆阻器，我们必须通过测量位线BL上的电压来读取数据，该电压由以下方程给出，

$$ V_{BL} = I_{memristor} \times (R_{MN2} + R_1) $$ (15)

$$ I_{memristor} = \frac{V_{DD}}{R_t} $$ (16)

其中，

$$ R_t = R_{MP2} + R + (R_{MP1} || R_{MN1}) + R_{MN2} + R_1 $$ (17)

其中 R是忆阻器的电阻。

$$ V_{BL} \geq V_{tn}, \text{如果存储的数据为} 0 $$ (18)

$$ V_{tp} \leq V_{BL} \leq V_{tn}, \text{如果存储的数据为} 1 $$ (19)

其中 $V_{tn}$、$V_{tp}$分别为 N型和 P型 MOSFET的阈值电压。

由(17)和(15)可知，忆阻器的电阻对电流具有反向影响，因此流经忆阻器的电流在导通状态下的值大于关断状态下的值（因为R ON = 100且R OFF = 10k）。由(15)可知，V BL也受到忆阻值的反向影响。显然，V BL的值永远不会是良好的“0 ′′ 或良好的“1 ′′ ，而只能是介于两者之间的中间值。因此，如果我们想要读取忆阻器中写入的数据，则必须连接一个附加电路，该电路能够根据忆阻器之前写入的数据，在输出端产生良好的“0”或良好的“1 ′′ ”。例如，假设存储单元中写入的数据为一，这意味着忆阻器处于关断状态，即V BL为低电平。由于要读取的数据与V BL互为互补，因此所需的附加电路是一个反相器，其栅极电压为V BL，而待读取的数据将作为其漏极电压输出。当然，为了使该电路正常工作，必须确保V BL能够超过反相器的阈值，这可通过MP9和MN9实现，如公式(18)和(19)所示，而该阈值由电阻R 1的值决定。

在传统的6T SRAM单元中，使用单个NMOS晶体管来访问存储单元内容，并通过灵敏放大器进行读取。如果位线和位线反相（BL与BLB）之间存在50毫伏的差异，灵敏放大器便可感知并解码存储单元内容。然而，所提出的设计在传输门（TG）中使用了两个晶体管。这是因为在通过感知反相器读取时，需要栅极电压> V_M（开关阈值电压= 0.49 V）才能使感知反相器发生翻转。在执行读操作时，V_DD通过MP2、忆阻器、TG和MN2连接到地。MP2和忆阻器上存在非零的电压降。因此，反相器栅极处可获得的电压低于V_DD。如果像SRAM单元一样仅使用一个NMOS访问晶体管，则在其上还会产生额外的V_tn压降。该压降将导致无法在反相器栅极获得高于V_M的电压。为了避免这种情况，采用传输门（TG）代替单一的NMOS访问晶体管。当然，使用两个MOSFET也存在缺点，其优势是以面积开销为代价的。

5. RRAM架构

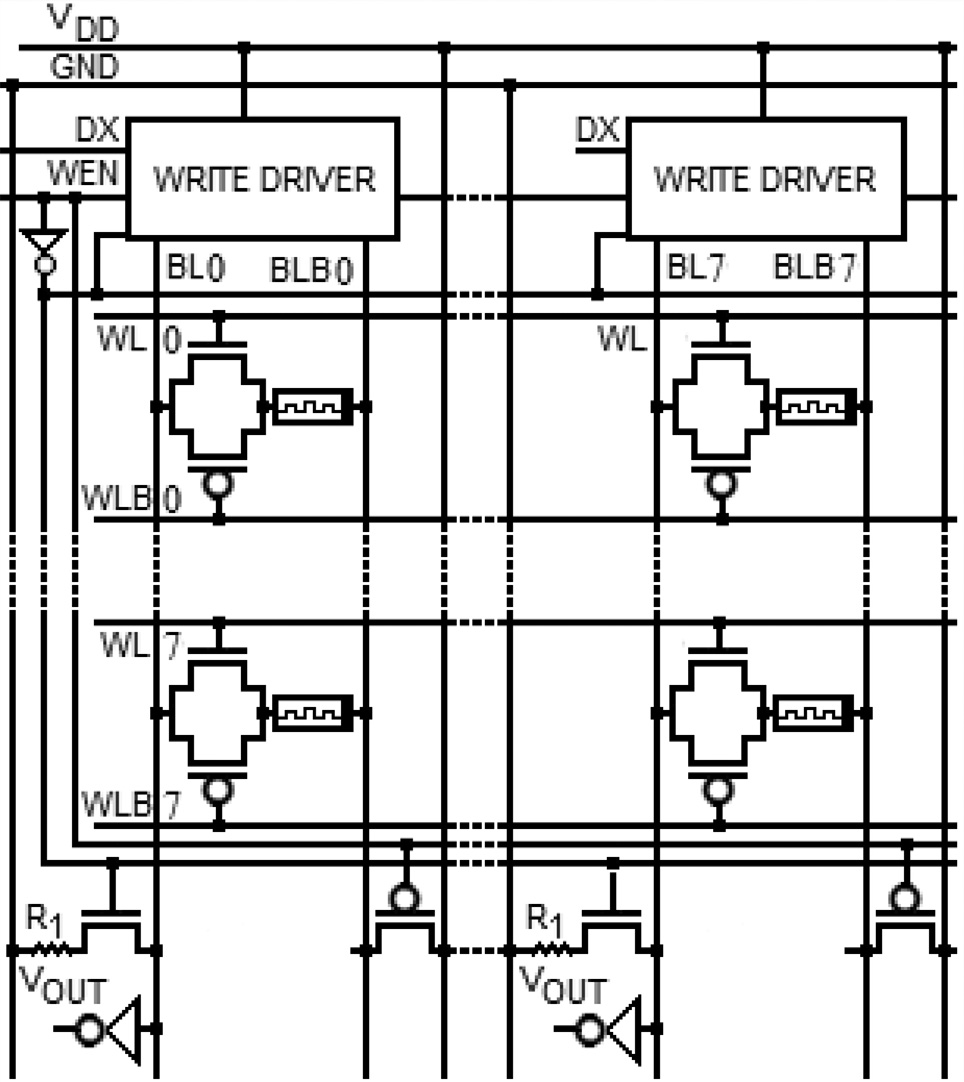
图7展示了所提出的8 × 8 RRAM单元的架构，其中每个RRAM单元可以通过字线和位线，利用列和行译码器进行访问。晶体管MN3、MN4、MN5、MN6、MN8、MP3、MP4、MP5、MP6和MP8被包含在写驱动器模块中，每一个的输入为DX、WEN和时钟信号，输出线为BL和BLB。晶体管MP7和MN7未包含在写驱动器模块中，因为该反相器的输出需要分别在读取和写入操作时控制读取电路中的晶体管MN2的导通与关断。由于在同一时刻仅有一行单元通过一条字线被选中，并激活一列中的一个单元，因此同一列的RRAM单元无需使用独立的位线。因此，每列单元配置一个写驱动器就已足够。同样，在读取操作中也只需要将读取电路连接到BL和BLB，因此每列单元只需一个读取电路即可，因为在同一时刻BL和BLB上的电压值仅由该列中唯一激活的RRAM单元的忆阻值决定。

该架构的整体位线和字线电容分别为104.8fF和5.832fF。由于对于任何内存架构而言，最小面积都是首要考虑因素（当然前提是存储单元正常工作），而RRAM单元仅包含一个忆阻器和一对访问晶体管，因此能够在很大程度上减小面积。由于写驱动器也是内存的关键部分，在其中选择晶体管的最小尺寸时，读取时间、写入时间与稳定性（与R ON和R OFF值之间的差异成正比）之间的平衡，对于任何架构同样重要。已进行相关仿真，下结果在表2中列出并展示（尺寸指写驱动器中晶体管的尺寸，W = L = 32 nm）。

Size	写0时间（纳秒）	写1时间（纳秒）	读0时间（纳秒）	读1时间（纳秒）
40 × W/L	8.5	5.4	8.2	5.1
60 × W/L	8.4	4.9	7.3	2.4
80 × W/L	7.6	4.9	2.1	2.4
100 × W/L	2.8	2.6	2	2.1

由于忆阻器与访问晶体管串联，流过访问晶体管的电流即为流过忆阻器的电流。由于访问晶体管的PMOS工作在线性区，因此有

$$ I_D = \mu C_{ox} \frac{W}{L} \left[ (V_{GS} - V_T)V_{DS} - \frac{V_{DS}^2}{2} \right] $$ (20)

其中 $I_D$为漏极电流 ， $\mu$为迁移率 ， $W$为晶体管的宽度 ， $L$为晶体管的长度 ，而 $V_T$为MOSFET的阈值电压 。

根据公式(20)，漏极电流取决于源极电压，在我们的电路中，该电压取决于写驱动器中晶体管的强度（尺寸= W/L）。晶体管尺寸越大，漏极电压向源极电压驱动的速度就越快。因此，晶体管尺寸与电流流动所需建立目标电压的时间之间形成反比关系（在写入情况下），这解释了随着晶体管尺寸增大，写入时间减少的原因（表2）。类似地，读取时间的减少也与晶体管尺寸相关。

保持功耗是指存储单元未被访问时内存所消耗的功率；即既不进行读操作也不进行写操作，而只是保持或存储单元内容时的功耗。大多数时间和内存中的大多数行都处于保持模式，因为在任一时刻只有一行被访问（即读取或写入）。然而，由于纳米级MOSFET中的漏电流，会产生静态或保持功耗。尽管待机模式最常用于处理器，但对于磁盘、有线和无线接口以及输入/输出设备等外围设备而言更为有意义，因为它们都是以突发模式运行的。例如，手机大部分时间都处于待机状态，即使在活动状态下，数据也只是周期性地传输。如果唤醒延迟和面积开销可以接受，那么使用睡眠晶体管的电源门控技术是降低功耗最有效的方法。然而，进入睡眠模式的电路模块必须能够在恢复时保留其先前的状态。这要求电路模块中包含非易失性元件[26, 27] 。我们提出的存储元件是忆阻器，它本质上具有非易失性。因此，可以采用电源门控技术来降低静态或保持功耗，从而实现较低的功耗。

6. 基于工艺、电压和温度参数变化的所提出电路的稳定性

如上所述，忆阻器是莱昂·楚阿（Leon Chua）于1971年预测的缺失的第四种基本无源电路元件[8] ，并由威廉姆斯等人在 2008 [10] , 中通过实验实现，近年来因其广泛的应用前景而开始受到越来越多的关注。目前，TiO₂薄膜的制造主要采用溅射沉积或原子层沉积（ALD）方法[9 , 10] ，这些沉积方法成本较高。因此，文献[18]中的作者通过热氧化沉积的Ti薄膜制备了基于TiOx的忆阻器，该方法是一种低温制造工艺（400°C），因而成本较低，并且与CMOS技术兼容。本工作中所使用的忆阻器模型[9 , 16]具有高可靠性，采用该模型设计的RRAM特性稳定。

PVT 变化基于 32纳米技术（所使用的 MOSFET 参数的 CMOS模型为亚利桑那州立大学（ASU）纳米级集成与建模组（NIMO）开发的 32 纳米预测技术模型（PTM））。忆阻器的尺寸为 100 × W/L（其中 W/L 为 = 32 nm/32 nm），开关阈值电压为 0.2 V。

)

的表示。)

6.1. 电压参数变化的影响

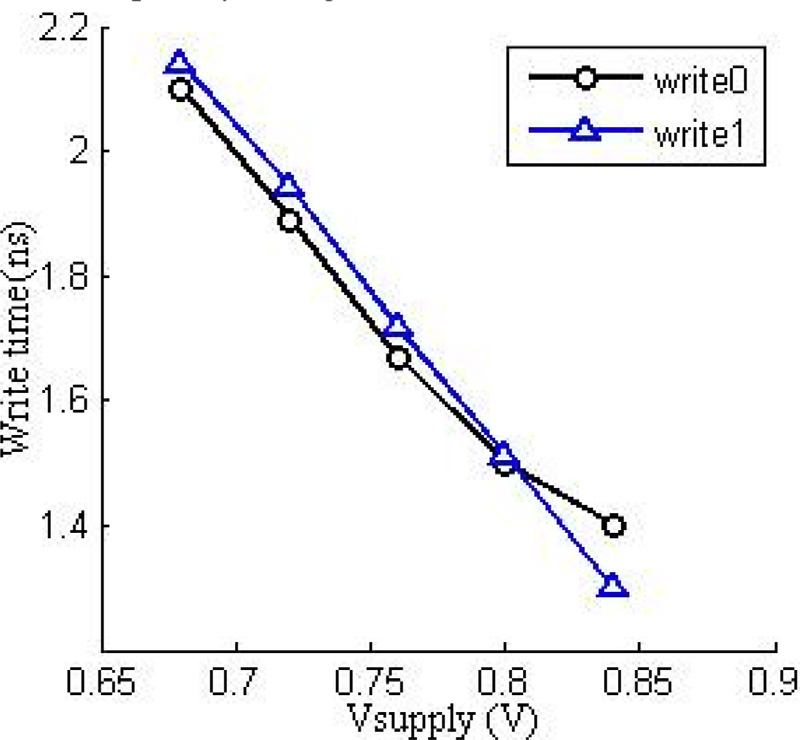
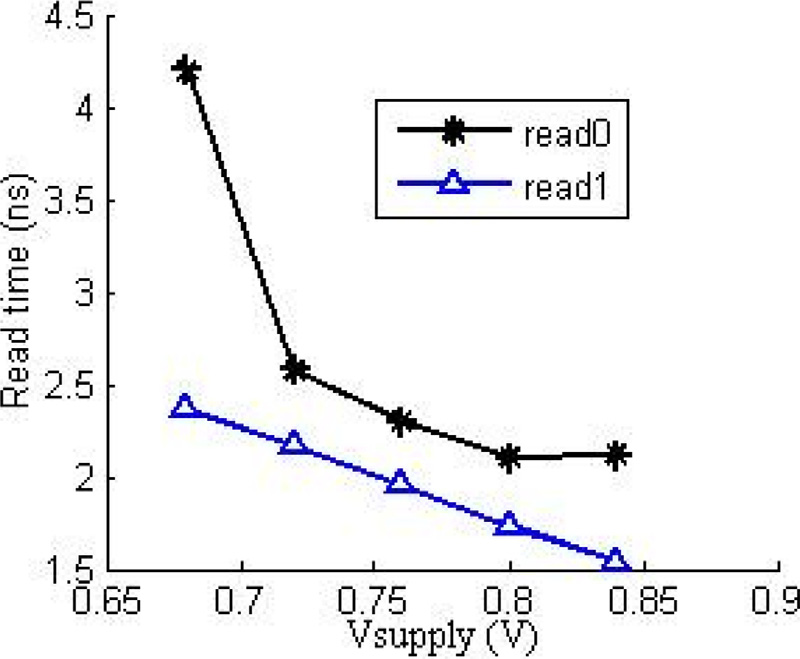
为了分析电路在电压变化下的稳定性，绘制了图8和图9所示的曲线。随着电源电压的增加，Vgs增大，导致写驱动器中PMOS电路初始流过忆阻器的饱和电流增加，同时Vds也增大，使线性电流增加。因此，流过忆阻器的总电流增加。由于写入电流(I(t))增大，掺杂层的变化率加快，写入时间减少。关于对读周期的影响，电源电压的增加会提升漏极电流，有助于BL节点处的电容器更快充电，从而更快地在位线BL上建立电压，进而缩短读取时间。

6.2. 温度参数变化

CMOS晶体管的阈值电压（V_T）随温度的变化特性被建模为[28]

$$ V_T(T) = V_T(T_0) + \alpha V_T (T - T_0) $$ (21)

其中 αVT 是阈值电压的温度系数，且 T₀ = 300 K。αVT 被假定为一个常数，其值在 −1 mV/°C 到 −4 mV/°C 之间变化，最常用的值为 −2 mV/°C [29] 。类似地，迁移率的温度依赖性建模为 [29]

$$ \mu_N(T) = \mu_N(T_0) \left( \frac{T}{T_0} \right)^{\alpha_\mu} $$ (22)

这里， αμ 是一个提取的参数，称为迁移率温度指数。此外，αμ 被建模为 s

$$ \alpha_\mu = \alpha_{\mu0} + \alpha_{\mu1} \left( \frac{\Delta T}{T_0} \right) $$ (23)

对于n沟道器件，αμ0 和αμ1 在NMOSFET [30] 中分别处于从−2.1到−1.9以及从−0.05到−0.01范围内的负值。然而，在建模时αμ 通常被视为常数。

式(21)和(22)表明，迁移率μ和阈值电压V_T均随温度升高而降低。然而，它们对CMOS晶体管的漏源电流I_DS具有相反的影响，该电流被建模为

$$ I_{DS} \propto \mu_N(T)[V_{GS} - V_T(T)]^\alpha $$ (24)

的写入时间表示。)

。)

其中，α被称为速度饱和指数。由于V_T 随温度升高而降低，导致I_DS 随温度升高而增加，但迁移率随温度升高而退化会降低I_DS 。然而，与V_T 变化对I_DS 的影响相比，迁移率随温度变化的影响占主导地位。因此，随着温度升高，电路的写入时间与读取时间（即写延迟和读延迟）因访问传输门（传输门）提供的驱动电流降低而增加（见图10和图11）。

因此，由式(3)我们可以得出 （假设 dx/dt= z ）如下结论

$$ \frac{dz}{dT} = \left( \frac{\partial z}{\partial u_v} \times \frac{du_y}{dT} \right) + \left( \frac{\partial z}{\partial I(t)} \times \frac{dI(t)}{dT} \right) $$ (25)

其中， du_v/dT为正[19]且 d(I(t))/dT为负[20] 。

$$ \frac{\partial z}{\partial u_v} = \frac{R_{on}}{D^2} \times W(x) \times I(t) $$ (26)

$$ \frac{\partial z}{\partial I(t)} = \frac{R_{on} \times u_y}{D^2} \times W(x) $$ (27)

因此，

$$ \frac{\partial z / \partial u_v}{\partial z / \partial I(t)} = \frac{I(t)}{u_v} $$ (28)

由于 I(t)是漏极电流 ，因此它将处于 范围 为 10⁻⁴安培[20], ，而 u_v的范围为 10⁻¹² m² s⁻¹ V⁻¹ [19] 。

因此,的范围为

$$ \frac{\partial z / \partial u_v}{\partial z / \partial I(t)} \leq 10^8 $$ (29)

因此，由于掺杂层的变化率随温度降低，du_v/dT 的影响大于 d(I(t))/dT，导致写入时间“t”随温度升高而增加。由于漏极电流随温度呈负向变化，读取时间在相对于温度作图时也呈现正斜率，如图10和图11所示。

的读0和读1的读取电流示意图)

6.3. 氧化物厚度参数变化的影响

32纳米技术代的纳米级CMOS晶体管的氧化层厚度小于一毫米，仅有几个原子距离。在制造CMOS晶体管时，精确地在多晶硅栅极下方施加相同数量的SiO₂原子层几乎是不可能的。制造过程中总会存在多形成或少形成一到两个原子层SiO₂的可能性。换句话说，在先进的CMOS工艺中，氧化层厚度的变化是不可避免的。这意味着位于硅衬底上相邻的CMOS晶体管可能具有不同的氧化层厚度，从而导致V_T变化。因此，为了考虑工艺变异的影响，我们通过改变氧化层厚度来估算读取电流。

为了分析存储单元对工艺变异（如tox变化）的稳定性（图12），绘制了写入电流与tox的关系图。由于氧化层的电容随tox增加而减小[19] ，导致写入时间减少。此外，tox的增加也会降低读取电路中MOSFET的漏极电流，从而如前所述缩短读取时间。这表明，提出的存储器单元由于在工艺变异（如氧化层厚度变化）下具有较低的读取电流变化，因而具备更好的稳定性。

7. 仿真方法与结果分析

为了模拟我们提出的忆阻器器件，采用了惠普实验室（HP Lab）提出的具有阈值电压型开关的双极性忆阻模型（在第二节B部分中说明）。提出存储器的读写时间已在上文列出（表3、表4）。该时间是在32纳米和45纳米技术节点下计算的（使用由亚利桑那州立大学（ASU）纳米级集成与建模组（NIMO）开发的预测技术模型（PTM）），电源电压分别为0.9 V、1 V、1.1 V，尺寸为100 × W/L（其中W/L为= 32 nm/32 nm），阈值电压为0.2 V。

所获得的结果与不同论文中提出的其他存储单元设计进行了比较，这些设计在结构中包含不同数量的忆阻器和晶体管，比较结果如下：

为评估所提出的存储单元架构的性能，本节对所提出的存储单元与其他已开发的基于忆阻器的存储器（如双极型晶体管存储单元[23]和MCAM[24] ）进行了比较（表6）。表5 [21]中将提出的存储器与另一种基于忆阻器的存储单元进行了对比。比较采用相同的工作电压0.9和32纳米技术的晶体管特征尺寸，结果如表6所示。由于所提出的存储单元中与忆阻器串联的晶体管数量较少，因此晶体管上的电压降较低，而忆阻器上的电压降较高，优于其他基于忆阻器的存储器架构[23] 。较大的电流使得掺杂层能根据电流方向快速增加或减少，从而在忆阻器两端电压较高的情况下实现忆阻值的快速变化

表 3 32纳米技术下的读写时间。
电压（Vdd）	写入1	写入0	读1	读0
0.9	2.28	2.9	4.10	2.89
1	2.27	2.9	3.78	2.78
1.1	2.34	2.71	3.74	2.71

表 4 在45纳米技术下的读写时间。
电压（Vdd）	写入1	写入0	读1	读0
0.9	2.28	2.89	3.74	3.28
1	2.28	2.88	3.73	3.18
1.1	2.26	2.77	3.10	3.11

表 5 基于写入和读取时间以及所用组件，将提出的存储器与其它 忆阻器基存储单元进行比较。
提出的存储器	内存 [21]
写入1(纳秒)	2.28	3.4
写入0(纳秒)	2.9	3.3
Read	3ns	100皮秒
晶体管	2	6
忆阻器	1	1

Table 6 基于读写时间与双极性存储器和MCAM的比较。
提出的存储器	内存 [22]	双极性存储器 [23]	MCAM [24]
Vdd	0.9V	0.9V	0.9V	0.9V
写入时间	2.8纳秒	10.04纳秒	219纳秒	51.2纳秒
读取时间	3.3 ns	0.6 ns	1.095 ns	12 ns

Table 7 与NAND和NOR闪存的读写时间比较。
提出的存储器	内存 [22]	NAND 闪存 [32, 33, 35]	NOR 闪存 [34, 36, 32]
写入时间	2.8纳秒	10.04纳秒	1/0.1毫秒	0.1毫秒/100毫秒
读取时间	3.3纳秒	0.6纳秒	0.1毫秒	100纳秒
写入电压	0.9	0.9	15	10
读取电压	0.9	0.9	1.8	1.8

在我们提出的设计中使用了忆阻器。这种高变化率的忆阻值有助于加快所提出电路的切换操作。数据检索通过检测所提出架构中的输出电压 V out 来完成。MCAM 中存储的数据需要与搜索数据进行匹配，以放电匹配线电压。因此，MCAM 中的状态检查通过搜索操作实现。所提出的存储单元不需要搜索操作，这使得读操作比 MCAM 更快 [24] 。此外，通过将所提出的存储单元与最近预测和制造的基于 NAND 和 NOR CMOS 的闪存进行比较来完成性能评估 [32–36] 。NAND 闪存的写入时间 1/0.1 ms 表示写入时间为 1 ms，擦除时间为 0.1 ms。

忆阻器的掺杂区包含氧空位（见图1），其行为类似于正电荷，当在其（+ ）端施加正电压时，这些氧空位被排斥，从而扩大掺杂区并降低其电阻值。氧空位的迁移率并不高，因此电阻变化发生得较慢，因而写入速度不高。尽管如此，与表7中比较的其他存储器（如NAND和NOR闪存）相比，所提出的存储单元的写入时间更短。

8. 结论

本文对基于传输门的2T1M RRAM位单元进行了分析。为了展示所提出位单元的鲁棒性和稳定性，在HSPICE中进行了仿真。SPICE仿真结果表明，由于所提出的存储单元在工艺变异下具有较低的读取电流变化，因此具备更好的稳定性。通过使用忆阻器作为存储元件并施加PVT变化，我们反映了读写时间等性能指标的改善。所提出的电路的读取时间相比传统SRAM显著更快，且功耗也较低。然而，由于我们所使用的SPICE模型中忆阻器的迁移率非常低，导致写入速度不够理想。最近的研究表明，通过采用最先进的制造技术和基于忆阻器的RRAM，可以将写入时间减少[23, 24] 。此外，在降低功耗方面仍有诸多研究空间。最后，可以说我们提出的基于忆阻器的RRAM结合了最新技术与创新设计，为存储器设计领域开辟了新的方向。因此，忆阻器内存可被视为现有动态随机存取存储器和闪存的有力竞争者，而基于忆阻器的RRAM位单元将在非易失性存储器件中变得更加流行。

所开发的电路在读操作期间能够防止存储单元最常见的状态漂移问题，并且在无需刷新的情况下连续读取操作时表现出很高的稳定性。该存储元件可用于加速高性能和高密度存储系统的设计与探索。