代码随想录算法训练营第24天

LeetCode 77. 组合

class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(int n,int k,int startindex){
    if(path.size()==k){
        result.push_back(path);
        return ;
    }
        for(int i=startindex;i<=n;i++){
            path.push_back(i);
            backtracking(n,k,i+1);
            path.pop_back();
        }
    }
    vector<vector<int>> combine(int n, int k) {
        backtracking(n,k,1);
        return result;
    }
};

剪枝优化

剪枝优化是理解的难点

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // 优化的地方
            path.push_back(i); // 处理节点
            backtracking(n, k, i + 1);
            path.pop_back(); // 回溯，撤销处理的节点
        }
    }
public:

    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;
    }
};

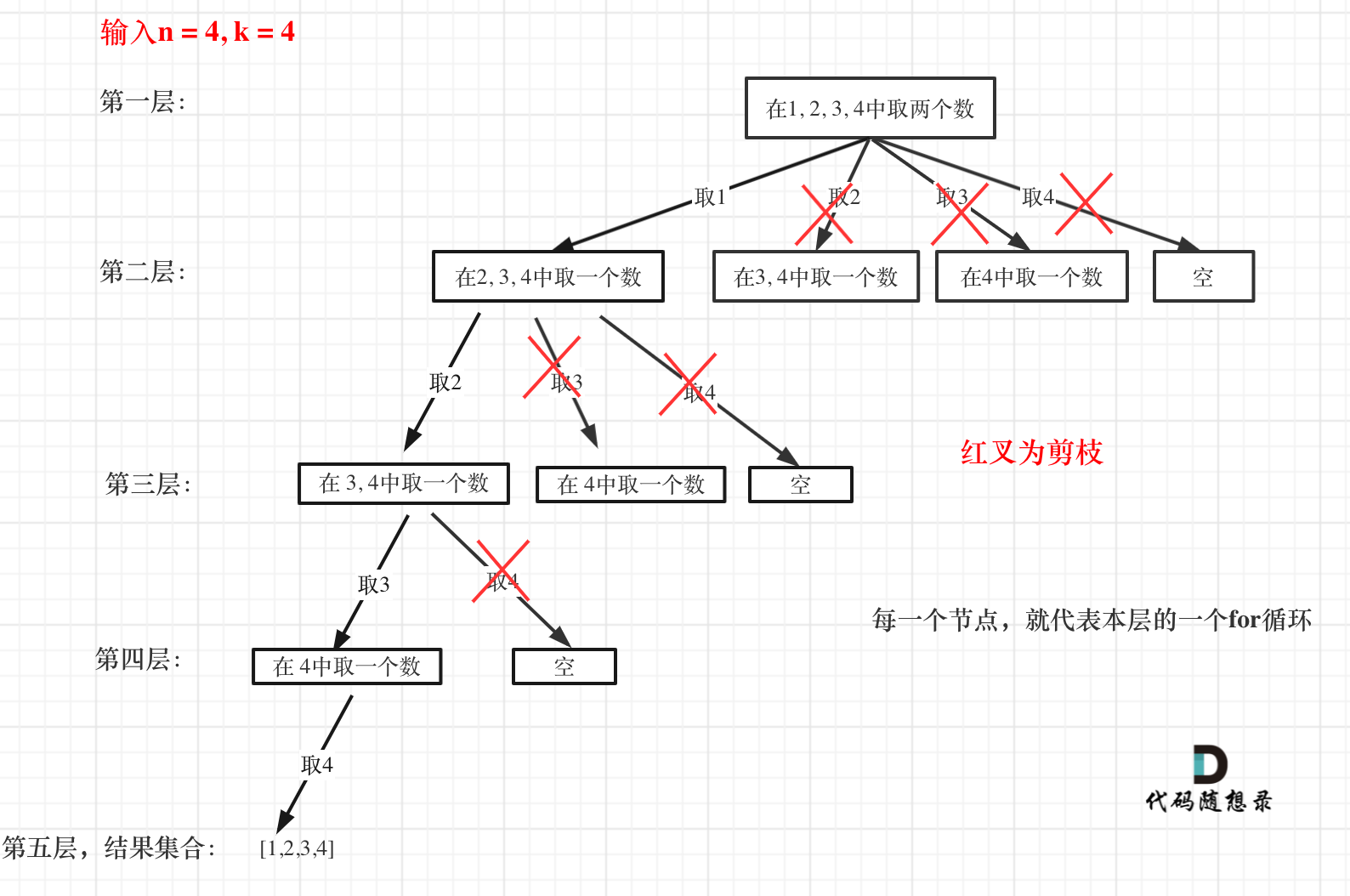
剪枝的依据原理：如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。

接下来看一下优化过程如下：

1. 已经选择的元素个数：path.size();
2. 还需要的元素个数为: k - path.size();
3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

1，2步都较为简单理解，但是第三步很难理解

理解：重点是上面的至多，说的比较抽象，自己想象一个数组，如1，2，3，4，n=4，k=4

设我们已经选取了1这个元素，path.size()=1，还需要的元素个数是3，

此时startindex位置就是2，2刚好是临界的n - (k - path.size()) + 1值

如果此时到3的话，就会到3，超出了2，此时直接可以舍去，就相当于此时树节点即以后的所有情况只保留一条边就行，其他的舍去，提高了效率。还是上面说的，n - (k - path.size()) + 1这个就是至多要开始的位置。