本文详细介绍了双指针技术在数组遍历、滑动窗口、有序数组合并及字符串处理等场景的应用，包括LeetCode上的经典问题。通过实例解析了如何使用双指针解决寻找两数之和、合并有序数组、最小覆盖子串等问题，以及如何优化算法以达到线性时间复杂度。同时，文章探讨了回文字符串验证、平方数之和判断等挑战，展示了双指针与其他数据结构结合的策略。
算法解释
双指针主要用于遍历数组，两个指针指向不同的元素，从而协同完成任务。也可以延伸到多个数组的多个指针。
若两个指针指向同一数组，遍历方向相同且不会相交，则也称为滑动窗口（两个指针包围的区域即为当前的窗口），经常用于区间搜索。
若遍历反向相反，则可以用来搜索有序数列。
指针有关内容复习
1.指针与常量
#define预处理与const关键字
要注意const类型定义的不能重定义，即不能修改
int *p=&x；//此种方式指针和值均可修改
const int *p2=&x;//此为一const int 类型的值，所以值不能被修改，指针可以
int * const p3=&x;//此为int类型的值，值可以被修改，而指针p3为const类型，不可修改
const int * const p4=&x;//此为const int 类型值，不可修改，为const类型指针，不可修改
2.指针与函数
指针函数是一个函数，返回的是指针，所以我们要用static或者new来防止局部变量地址不能被返回的问题。（详情见新发布的文章有讲new的）
而函数指针是一个指针，其指向某个函数。
int sub(int a,int b) //先定义一个普通减法
{
return a-b;
}
int (*m)(int,int)=sub; //m为一个函数指针，指向sub，参数为两个int
//接下来我们就可以定义某个操作，用函数指针调用
int operation(int x,int y,int (*func)(int,int))//定义操作，对象为xy，功能为指针型
{
return （*func)(x,y);//对xy进行func指向的函数的操作
}
//可以在main函数中如下使用：
int n=operation(3,5,m);
例：leetcode167.两数之和
给定一个已按照升序排列 的有序数组，找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。
说明:
返回的下标值（index1 和 index2）不是从零开始的。
你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。
分析：
因为数组已经升序，我们定义两个指针，一个在最左向右跑，一个在最右向左跑。
那么这两个指针对应的值的和，无非就三种情况：
1.两数之和刚好等于target，输出两指针位置，注意题目中从1开始数，所以每个指针都+1。
2.如果>target，说明右边大的数大了，把右指针左移一次即可。（这个很好理解，因为你左指针如果右移只会更大）。
3.如果<target，说明左边小的数小了，把左指针右移一次即可。
代码：
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
int s=numbers.size();
int l=0; int r=s-1;
int sum;
while(l<r)
{
sum=numbers[l]+numbers[r];
if(sum==target) break;
if(sum<target) l++;
else r--;
}
return vector<int>{l+1,r+1};
}
};
例：88合并两个有序数组
给你两个有序整数数组 nums1 和 nums2，请你将 nums2 合并到 nums1 中，使 nums1 成为一个有序数组。
初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。你可以假设 nums1 的空间大小等于 m + n，这样它就有足够的空间保存来自 nums2 的元素。
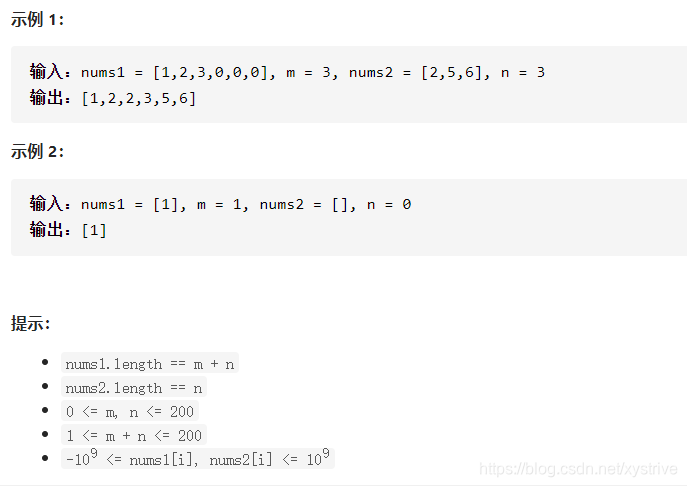
分析：这一题上来可能有想法从开头开始，按小的插入，但是这样比较的话有一个弊端在于，没有利用好他给的m和n，而且不太好判断何时结束。于是我们想到把m和n作为双指针p1,p2，并且在nums1的末尾再加入第三个指针p3。
我们每次比较p1,p2如果p2大，就把p3的位置变成p2，p2 p3都自减
如果p1大，把p3位置变成p1，p1 p3自减
所以这个循环用while比较合适，一直跑到while(m>=0 &&n>=0),但是，是不是这种情况就跑完了呢？非也
因为如果出现两个数组一长一短的情况，其中有一个会先跑完。我们来想一下这是个什么情况：
1.如果m长n短，因为我们每次是把n的元素插入m，这时必定已经插入完成了，而m本身已经是升序的，所以这是正常情况
2.如果n长m短呢，这个时候我们发现还有n的部分元素没有被插入进去第一个while已经结束，所以我们需要第二个while把n跑完，每次把p3的位置变成p2，然后p2p3自减一直到n=0。
我们发现逻辑是这样的，谁大p3=谁，且p3每次都自减，谁大谁自减，这个可以这样表达：（注意这里要用后加，因为是比较完了再进行自加和自减）
nums1[p3--]=nums1[m]>nums2[n]? nums1[m--]:nums2[n--];
代码：
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int p3=m+n-1;
m--;
n--;
while(m>=0 && n>=0)
{
nums1[p3--]=nums1[m]>nums2[n]? nums1[m--]:nums2[n--];
}
while(n>=0)
{
nums1[p3--]=nums2[n--];
}
}
};
滑动窗口：
例：76最小覆盖子串
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。
注意：如果 s 中存在这样的子串，我们保证它是唯一的答案。
进阶：你能设计一个在 o(n) 时间内解决此问题的算法吗？
分析：
首先是统计字符的情况，因为我们知道因为 ASCII 只有256个字符，所以用个大小为 256 的 int 数组即可代替 HashMap，但由于一般输入字母串的字符只有 128 个，所以也可以只用 128，所以我们建立一个数组来统计T种字符情况：
注意：T当中可能有重复字符的。
vector<int> chars(128,0);
for(char c:t) ++chars[c]; //统计t中每个字符有多少
这一题中我们使用滑动窗口的思想在于，我们先找到一个包含T中所有元素的最长字符串，然后再从左缩小窗口，得到最短字符串。即先扩大右边界，然后再收缩左边界。
开始遍历S串，对于S中的每个遍历到的字母，都在 chars数组中减1，如果减1后的映射值仍大于等于0，说明当前遍历到的字母是T串中的字母，使用一个计数器 cnt，使其自增1。当 cnt 和T串字母个数相等时，说明此时的窗口已经包含了T串中的所有字母。我们下一步只需要进行缩小左窗口。
没有必要每次都计算子串，只要有了起始位置和长度，就能唯一的确定一个子串。这里使用一个全局变量 minLeft 来记录最终结果子串的起始位置，初始化为 -1，最终配合上 minLen，就可以得到最终结果了。注意在返回的时候要检测一下若 minLeft 仍为初始值 -1，需返回空串，
代码：
class Solution {
public:
string minWindow(string s, string t) {
vector<int> chars(128,0);
for(char c:t) ++chars[c]; //统计t中每个字符有多少
int left=0,count=0,minleft=-1,minsize=s.size()+1;
for(int i=0;i<s.size();++i)//i代表右边界
{
//s中的每一个元素，对应到chars中，如果t中有，把chars减一，如果减一之后还大于0，计数器+1
if(--chars[s[i]]>=0)
++count;
//若r已经右移到右边界，但注意此时chars并不是所有元素都被取0了，可能有多出来的元素>0
//此时的count应该和t.size()相等
while(count==t.size())//开始左移左窗口以缩小得到最短字符串
{
if(minsize>i-left+1) //缩短minsize
{
minsize=i-left+1; //winsize就是-left+1
minleft=left; //更新左窗口指针
}
if(++chars[s[left]]>0) --count;
++left;
}
}
return minleft==-1? "":s.substr(minleft,minsize);//子串从minleft开始，长度为minsize
}
};
练习
633平方数之和
给定一个非负整数 c ，你要判断是否存在两个整数 a 和 b，使得 a2 + b2 = c 。
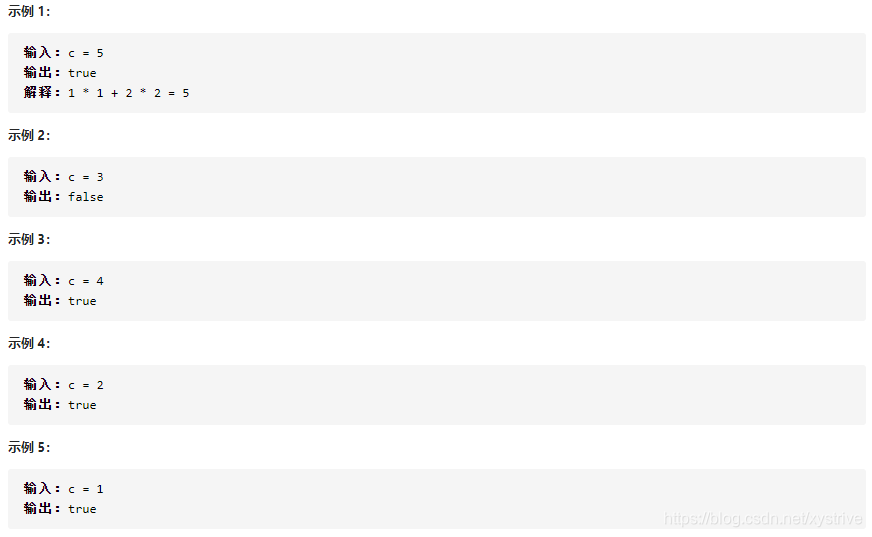
分析： 很明显用双指针，第一个指针自然是从0开始往右移动。
而至于b，b=c-a方 再开方，从这个点往左走。然后b又要是个整数，刚才开放之后不一定是整数，所以开方完了要向下取整，此时还得是个正数才行。
如果ab的平方和比c小，那左边加一。
如果ab的平方和比c大，那么右边减一。
注意：
因为他给出的测试用例很大，所以我们用int类型是不够的。所以我用的long int ，因为之前用int提交的溢出了。
代码：
class Solution {
public:
bool judgeSquareSum(int c)
{
long int a=0;
long int b=floor(sqrt(c-a*a));
long int d;
while(a<=b)
{
d=a*a+b*b;
if(d==c)
return true;
if(a*a+b*b<c)
++a;
if(a*a+b*b>c)
--b;
}
return false;
}
};
680验证回文字符串 Ⅱ
给定一个非空字符串 s，最多删除一个字符。判断是否能成为回文字符串。
分析：
其实这一题有两个需求，
- 第一个需求是要判断某一个字符串是不是回文字符串
- 第二个需求是我们删除一个字符其是不是。。。
所以感觉上加一个判断是否是回文字符串的子函数比较方便一些。
首先我个人觉得既然已经多写了一个函数，那么干脆多返回几个值，所以这个函数不光是要bool的结果，我还要两个不等的位置l和r。（另一方面这大大增加了空间开销）
函数返回多个值可以用
return std::make_tuple(x,x,x);
再用
auto[x,x,x]=f();
接回来返回的数值即可。
然后呢，如果其不是回文字符串，只有两个可能性：
- 删除左边l位的字符即可回文，所以此时我们只需要检查l+1到r
- 删除右边r位的字符即可回文，所以我们检查l到r-1
所以总代码如下：
class Solution {
public:
auto checkhw(string s,int l,int r)
{
while(l<=r)
{
if(s[l]!=s[r])
return std::make_tuple(0,l,r);
++l;--r;
}
return std::make_tuple(1,l,r);;
}
bool validPalindrome(string s)
{
auto [a,l,r]=checkhw(s,0,s.size()-1);
if(a) return true;
auto[a1,l1,r1]=checkhw(s,l+1,r);
if(a1) return true;
auto[a2,l2,r2]=checkhw(s,l,r-1);
if(a2) return true;
return false;
}
};
这个代码写的不好，空间开销太大了，但是时间开销非常不错，算是拿空间换时间吧。
524通过删除字母匹配到字典里最长单词
给定一个字符串和一个字符串字典，找到字典里面最长的字符串，该字符串可以通过删除给定字符串的某些字符来得到。如果答案不止一个，返回长度最长且字典顺序最小的字符串。如果答案不存在，则返回空字符串。
分析：
1.先给这个字典按长度排个序，如果出现一样长的就按升序排，题目给出的示例2应该是这个意思。
这个排序稍稍有些复杂，先写一下吧：
sort(dictionary.begin(),dictionary.end(),[](string a,string b)
{
if(a.size()!=b.size()) return a.size()>b.size();
return a<b;
}
);
2.对于排序好的d，里面每一个字符串，都双指针，一个指针i指在s开头，另一个指针j指在字符串p开头。
- if(i !=j) ++i;
- else ++i,++j;
- 如果i在s里先跑完，说明不是
- 如果j在p里先跑完,且s里后面能有和p的最后一个相等的，即s[i]==dictionary[p][j]，输出
代码：
class Solution {
public:
string findLongestWord(string s, vector<string>& dictionary)
{
sort(dictionary.begin(),dictionary.end(),[](string a,string b)
{
if(a.size()!=b.size()) return a.size()>b.size();
return a<b;
}
);
int l=s.size()-1;
for(int p=0;p<dictionary.size();++p)
{
int i=0,j=0;
while(i<s.size()&& j<dictionary[p].size())
{
if(j==dictionary[p].size()-1 &&s[i]==dictionary[p][j])
return dictionary[p];
if(s[i]!=dictionary[p][j]) ++i;
else
{
++i;++j;
}
}
}
return "";
}
};
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
