二叉树遍历--非递归

二叉树遍历–非递归
非递归vs递归
非递归 ：栈空间更容易控制，栈的空间在堆上，一般比较大。
递归 :    使用的栈是系统调用栈，往往空间比较小
        一般比较难固定大小。

前序遍历
访问根结点的操作发生在遍历其左右子树之前。（回溯）

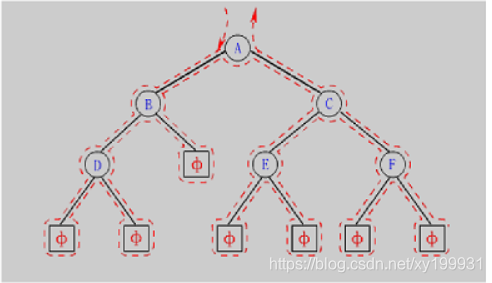
由上图，每个结点均被访问了三次，因遍历的时候遵循 根+左+右，即第一次访问时就打印，就是前序遍历。
思路

1. 从根结点 cur遍历，依次遍历每个结点的 left（如图左边的线路）
   两个操作：打印，入栈
2. 当cur == null 时，即每个结点的左子树那边访问了依次
   执行出栈检索
   访问结点的右子树线路
3. 循环条件
   栈不为空 或 cur != null

主要代码

public static void preorderNoR(TreeNode root){
    Stack<TreeNode> stack=new Stack<>();
    TreeNode cur=root;
    while(!stack.empty()||cur!=null){
        while(cur!=null){
            System.out.println(cur.val);
            stack.push(cur);
            cur=cur.left;
        }
        TreeNode top=stack.pop();
        cur=top.right;
    }
}

中序遍历
访问根结点的操作发生在其左右子树之间。
即上图的第二次访问（出栈）时打印

主要代码

public static void inorderNoR(TreeNode root){
    Stack<TreeNode> stack=new Stack<>();
    TreeNode cur=root;
    while(!stack.empty()||cur!=null){
        while(cur!=null){
            stack.push(cur);
            cur=cur.left;
        }
        TreeNode top=stack.pop();
        System.out.println(top.val);
        cur=top.right;
    }
}

后序遍历
第三次访问时打印
三次完整经过点：1. 出栈后 right==null
                 2. 结点的 right 是上一个被三次完整访问的点

主要代码

public static void postorderNoR(TreeNode root){
            Stack<TreeNode> stack=new Stack<>();
            TreeNode cur=root;
            TreeNode last=null; //上一个被三次完整经过的点
            while(!stack.empty()||cur!=null) {
                while (cur != null) {
                    stack.push(cur);
                    cur = cur.left;
                }
        TreeNode top = stack.peek();
        if (top.right == null || top.right == last) {
            stack.pop();
            System.out.println(top.val);
            last = top;
        }else{
            cur=top.right;
        }
    }
}