（1）插入排序、合并、快速排序运行时间与排序元素个数的统计比较；（2）阐述比较结果。（3）利用算法采用的设计方法，时间复杂度等分析得到该结果的原因。

插入排序代码：

// 直接插入排序
void insertionSort1(int A[], int n) {
    for (int i = 1; i < n; i++) {
        int temp = A[i];
        int j = i - 1;
        while (j >= 0 && A[j] > temp) {
            A[j + 1] = A[j];
            j = j - 1;
        }
        A[j + 1] = temp;
    }
}

插入排序结果（部分）：

合并排序代码：

// 合并排序
void merge(int B[], int p, int C[], int q, int A[]) {
    int i = 0, j = 0, k = 0;
    while (i < p && j < q) {
        if (B[i] <= C[j]) {
            A[k] = B[i];
            i++;
        }
        else {
            A[k] = C[j];
            j++;
        }
        k++;
    }
    while (i < p) {
        A[k] = B[i];
        i++;
        k++;
    }
    while (j < q) {
        A[k] = C[j];
        j++;
        k++;
    }
}

void mergeSort(int A[], int n) {
    if (n > 1) {
        int mid = n / 2;
        int* B = (int*)malloc(mid * sizeof(int)); // 动态分配内存给B
        int* C = (int*)malloc((n - mid) * sizeof(int)); // 动态分配内存给C

        for (int i = 0; i < mid; i++) {
            B[i] = A[i];
        }

        for (int i = mid; i < n; i++) {
            C[i - mid] = A[i];
        }

        mergeSort(B, mid);
        mergeSort(C, n - mid);

        merge(B, mid, C, n - mid, A);

        free(B); // 释放B数组的内存
        free(C); // 释放C数组的内存
    }
}

合并排序结果（部分）：

快速排序代码：

void swap(int* a, int* b) {
    int t = *a;
    *a = *b;
    *b = t;
}

int partition(int A[], int l, int r) {
    int p = A[l];
    int i = l, j = r + 1;

    while (1) {
        do {
            i++;
        } while (A[i] < p);

        do {
            j--;
        } while (A[j] > p);

        if (i >= j) {
            break;
        }
        swap(&A[i], &A[j]);
    }
    swap(&A[l], &A[j]);
    return j;
}

快速排序结果（部分）：

插入排序和合并排序、快速排序n（0<n<5000）个数时间效率对比:

实验结果：由运行结果可视化分析可以得出，当n逐渐增大后，直接插入排序所花费的时间明显高于合并和快速排序的时间。

原因分析：

1. 合并排序

合并排序将待排序的数组不断地分割成小的数组，然后再合并这些小数组以得到最终的有序数组。使得整体的时间复杂度较低。其时间复杂度为O(n log n)，因为每一次合并操作都涉及到n个元素，而总共需要进行log n次合并操作。

1. 插入排序：

由于直接插入排序每次只能将一个元素插入到已排序序列中，因此在平均情况下需要进行n^2/4次比较和n^2/4次移动。假设要被排序的序列中由n个数，遍历一趟的时间复杂度为O（n），一共需要遍历n-1次所以插入排序的时间复杂度是O(N^2)。

1. 快速排序：

在平均情况下，快速排序的时间复杂度为O(nlogn)，其中n是待排序数组的长度。因为在每一次分区操作中，将数组分成两部分的时间复杂度为O(n)，而整个数组需要进行logn次分区操作。在最坏情况下，快速排序的时间复杂度为O(n^2)。最坏情况发生在每次分区操作都选择了当前序列中的最大或最小元素作为基准元素，导致分区不平衡。

下图是nlogn和n^2复杂度算法效率对比

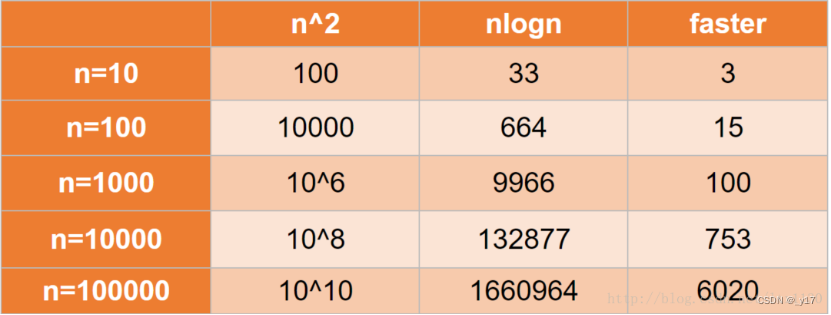
源码：

#include <stdio.h>
#include <time.h>
#include <stdlib.h>

void swap(int* a, int* b) {
    int t = *a;
    *a = *b;
    *b = t;
}

int partition(int A[], int l, int r) {
    int p = A[l];
    int i = l, j = r + 1;

    while (1) {
        do {
            i++;
        } while (A[i] < p);

        do {
            j--;
        } while (A[j] > p);

        if (i >= j) {
            break;
        }
        swap(&A[i], &A[j]);
    }
    swap(&A[l], &A[j]);
    return j;
}

void quickSort(int A[], int l, int r) {
    if (l < r) {
        int s = partition(A, l, r);
        quickSort(A, l, s - 1);
        quickSort(A, s + 1, r);
    }
}

int main() {
    int size = 1000;
    int* A = (int*)malloc(size * sizeof(int));
    // 生成随机数组A
    for (int i = 0; i < size; i++) {
        A[i] = rand();
    }

    clock_t start, end;

    // 快速排序算法
    printf("快速排序的运行时间:\n");
    for (int j = 0; j < size; j++) {
        start = clock();
        quickSort(A, 0,size-1);
        end = clock();
        printf("第%d个数的运行时间: %f 秒\n", j + 1, (double)(end - start) / CLOCKS_PER_SEC);
    }
    
    return 0;
}