一元线性回归是数据挖掘的基础模型,其中包含了非常重要的数学回归的概念,是学习多元回归,广义线性回归的基础。本文主要讲解1)基础原理2)数学推导3)R语言演示,来介绍一元线性回归。
整体思路:
根据已知点求一条直线,希望直线与各个点距离之和为最小,根据最小二乘法算出最小时直线的参数。
一、基础原理
例1 假设你想计算匹萨的价格。虽然看看菜单就知道了,不过也可以用机器学习方法建一个线性回归模
型,通过分析匹萨的直径与价格的数据的线性关系,来预测任意直径匹萨的价格。
| 直径(英寸) | 价格(美元) |
|---|---|
| 6 | 7 |
| 8 | 9 |
| 10 | 13 |
| 14 | 17.5 |
| 18 | 18 |
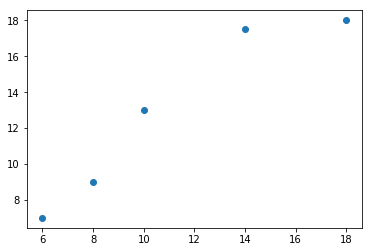
画出散点图
import matplotlib.pyplot as plt
import numpy as np
x=np.array([6,8,10,14,18])
y=np.array([7,9,13,17.5,18])
plt.scatter(x,y)
plt.show()
二 数学推导1
求J(θ)=12M∑i=1m(yi−a−bxi)2,θ={a,b}J(\theta)=\frac{1}{2M}\sum\limits_{i=1}^m(y_i-a-bx_i)^2,\theta=\{a,b\}J(θ)=2M1i=1∑m(yi−a−bxi)2,θ={a,b}的最小值?,这里J(θ)J(\theta)J(θ)称为损失函数.
求解过程:
$
\frac{\partial J(\theta)}{\partial a}=\frac{1}{2M}\sum\limits_{i=1}m2(y_i-a-bx_i)(-1)=-\frac{1}{M}\sum\limits_{i=1}m(y_i-a-bx_i)=-\frac{1}{M}(\sum\limits_{i=1}my_i-na-b\sum\limits_{i=1}mx_i)
$
$
\frac{\partial J(\theta)}{\partial b}=\frac{1}{2M}\sum\limits_{i=1}m2(y_i-a-bx_i)(-x_i)=-\frac{1}{M}\sum\limits_{i=1}m(y_i-a-bx_i)x_i
$
$
=-\frac{1}{M}\sum\limits_{i=1}m(x_iy_i-ax_i-bx_i2)=-\frac{1}{M}(\sum\limits_{i=1}mx_iy_i-a\sum\limits_{i=1}mx_i-b\sum\limits_{i=1}mx_i2)=0
$
即:
$
\left{\begin{array}{l}
\sum\limits_{i=1}my_i-ma-b\sum\limits_{i=1}mx_i=0\
\sum\limits_{i=1}mx_iy_i-a\sum\limits_{i=1}mx_i-b\sum\limits_{i=1}mx_i2=0
\end{array}\right.
$
解得:
$
a=\frac{\sum\limits_{i=1}my_i-b\sum\limits_{i=1}mx_i}{m}
$
$
b=\frac{m\sum\limits_{i=1}mx_iy_i-\sum\limits_{i=1}my_i\sum\limits_{i=1}mx_i}{m\sum\limits_{i=1}mx_i2-(\sum\limits_{i=1}mx_i)^2}
$
注: 上式可以写成
$
\left{\begin{array}{l}
a=\bar{y}-b\bar{x}\
b=\frac{\sum\limits_{i=1}^m(x_i-\bar x)(y_i-\bar{y})}{\sum\limits_{i=1}m(x_i-\bar{x})2}
\end{array}\right.
$
由下面可知,a,b的值还可写成
$
\left{\begin{array}{l}
a=\bar{y}-b\bar{x}\
b=\frac{cov(x,y)}{var(x)}
\end{array}\right.
$
利用公式
$
\left{\begin{array}{l}
a=\bar{y}-b\bar{x}\
b=\frac{cov(x,y)}{var(x)}
\end{array}\right.
$可得
xbar = (6+8+10+14+18)/5
ybar = (7 + 9 + 13 + 17.5 + 18) / 5
cov = ((6 - xbar) * (7 - ybar) + (8 - xbar) * (9 - ybar) + (10 - xbar) *(13 - ybar) +(14 - xbar) * (17.5 - ybar) + (18 - xbar) * (18 - ybar)) / 4
var_x=((6-xbar)**2+(8-xbar)**2+(10-xbar)**2+(14-xbar)**2+(18-xbar)**2)/4
print(cov,var_x)
结果为22.65,23.2.
Numpy里面有cov方法可以直接计算协方差
import numpy as np
xfc=np.cov([6, 8, 10, 14, 18], [7, 9, 13, 17.5, 18])
xfc
结果为
array([[23.2 , 22.65],
[22.65, 24.3 ]])
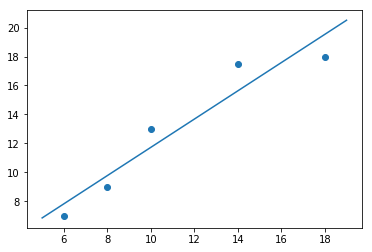
最后得到,b=cov(x,y)var(x)=22.6523.2=0.976,a=yˉ−axˉ=1.965b=\frac{cov(x,y)}{var(x)}=\frac{22.65}{23.2}=0.976,a=\bar{y}-a\bar{x}=1.965b=var(x)cov(x,y)=23.222.65=0.976,a=yˉ−axˉ=1.965,画出图形如下:
import matplotlib.pyplot as plt
import numpy as np
x=np.array([6,8,10,14,18])
y=np.array([7,9,13,17.5,18])
a=1.965;b=0.976
plt.scatter(x,y)
x1=np.linspace(5,19,100)
y1=a+b*x1
plt.plot(x1,y1)
plt.show()
在看一个例子.
例2 数据如下:
x,y
8.8,7.55
9.9,7.95
10.75,8.55
12.3,9.45
15.65,13.25
16.55,12.0
13.6,11.9
11.05,11.35
9.6,9.0
8.3,9.05
8.1,10.7
10.5,10.25
14.5,12.55
16.35,13.15
17.45,14.7
19.0,13.7
19.6,14.4
20.9,16.6
21.5,17.75
22.4,18.1
23.65,18.75
24.9,19.6
25.8,20.3
26.45,20.7
28.15,21.55
28.55,21.4
29.3,21.95
29.15,21.0
28.35,19.95
26.9,19.0
26.05,18.9
25.05,17.95
23.6,16.8
22.05,15.55
21.85,16.1
23.0,17.8
19.0,16.6
18.8,15.55
19.3,15.1
15.15,11.9
12.05,10.8
12.75,12.7
13.8,10.65
6.5,5.85
9.2,6.4
10.9,7.25
12.35,8.55
13.85,9.0
16.6,10.15
17.4,10.85
18.25,12.15
16.45,14.55
20.85,15.75
21.25,15.15
22.7,15.35
24.45,16.45
26.75,16.95
28.2,19.15
24.85,20.8
20.45,13.5
29.95,20.35
31.45,23.2
31.1,21.4
30.75,22.3
29.65,23.45
28.9,23.35
27.8,22.3
求出a,b的代码如下:
res=[]
with open('d:/shuju1.txt','r') as f:
lines=f.readlines()
for line in lines:
res.append(list(map(float,line.strip('\n').split(','))))
res=np.array(res)
xfc=np.cov(res[:,0],res[:,1])
x_mean=np.mean(res[:,0])
y_mean=np.mean(res[:,1])
b=xfc[0][1]/xfc[0][0]
a=y_mean-b*x_mean
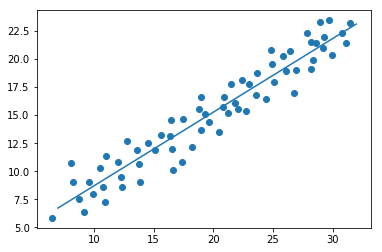
画出图如下:
plt.scatter(res[:,0],res[:,1])
x1=np.linspace(np.min(res[:,0])+0.5,np.max(res[:,0])+0.5,100)
y1=a+b*x1
plt.plot(x1,y1)
plt.show()
三 数学推导2
令J(θ)=12M∑i=1n(yi−(a+bxi))2=12M(y−xθ)T(y−xθ)J(\theta)=\frac{1}{2M}\sum\limits_{i=1}^n(y_i-(a+bx_i))^2=\frac{1}{2M}(y-x\theta)^T(y-x\theta)J(θ)=2M1i=1∑n(yi−(a+bxi))2=2M1(y−xθ)T(y−xθ),
对J(θ)J(\theta)J(θ)求一阶偏导得到梯度,
$
\begin{array}{lll}
\nabla_{\theta}J(\theta)&=&\nabla_{\theta}(\frac{1}{2}(y-x\theta)^T(y-x\theta))\
&=&\nabla_\theta(\frac{1}{2M}(yT-\thetaTx^T)(y-x\theta))\
&=&\frac{1}{2M}\nabla_\theta(yTy-yTx\theta-\thetaTxTy+\thetaTxTx\theta)\
&=&\frac{1}{2M}(-(yTx)T-xTy+2xTx\theta)\
&=&\frac{1}{M}(xTx\theta-xTy)=0
\end{array}
$
解得: θ=(xTx)−1xTy\theta=(x^Tx)^{-1}x^Tyθ=(xTx)−1xTy,这个结果对于多元线性回归也适用.
对于上面的例1,有
import matplotlib.pyplot as plt
import numpy as np
x=np.array([6,8,10,14,18])
y=np.array([7,9,13,17.5,18])
X=np.matrix([[1,6],[1,8],[1,10],[1,14],[1,18]])
Y=np.matrix([[7,9,13,17.5,18]]).T
theta=(X.T*X).I*(X.T*Y)
theta
结果为:
matrix([[1.96551724],
[0.9762931 ]])
对于上面的例2,有
res=[]
with open('d:/shuju1.txt','r') as f:
lines=f.readlines()
for line in lines:
res.append(list(map(float,line.strip('\n').split(','))))
res=np.array(res)
t=np.matrix([[1]*67])
X=np.hstack((t.T.A,np.matrix(res[:,0]).T.A))
X=np.matrix(X)
Y=np.matrix(res[:,1]).T.A
Y=np.matrix(Y)
(X.T*X).I*(X.T*Y)
结果为:
matrix([[2.10892056],
[0.65771558]])
3.1 梯度下降法
最小二乘法的弊端:最小二乘法可以一步到位,直接算出a和b,但他是有前提的,需要求(xTx)−1(x^Tx)^{-1}(xTx)−1,并且计算量大.
下面讨论不适用最小二乘法,而是梯度下降法来实现线性回归.
讨论损失函数J(θ)=12M∑i=1m(yi−(a+bxi))2J(\theta)=\frac{1}{2M}\sum\limits_{i=1}^m(y_i-(a+bx_i))^2J(θ)=2M1i=1∑m(yi−(a+bxi))2.
$
\frac{\partial J(\theta)}{\partial a}=\frac{1}{2M}\sum\limits_{i=1}m2(y_i-a-bx_i)(-1)=-\frac{1}{M}\sum\limits_{i=1}m(y_i-a-bx_i)
$
$
\frac{\partial J(\theta)}{\partial b}=\frac{1}{2M}\sum\limits_{i=1}m2(y_i-a-bx_i)(-x_i)=-\frac{1}{M}\sum\limits_{i=1}m(y_i-a-bx_i)x_i
$
我们要去找J(θ)J(\theta)J(θ)这个方程的最小值,最小值怎么求?按数学的求法就是最小二乘法呗,但是大家可以直观的想一下,很多地方都会用一个碗来形容,那我也找个碗来解释吧。

大家把这个Loss函数想象成这个碗,而我们要求的最小值就是碗底。假设我们现在不能用最小二乘法求极小值,但是我们的计算机的计算能量很强,我们可以用计算量换结果,不管我们位于这个碗的什么位置,只要我们想去碗底,就要往下走。
往下走????????这个下不就是往梯度方向走吗?
梯度不就是上面那两个公式呗。现在梯度有了,那每次滑多远呢,一滑划过头了不久白算半天了吗,所以还得定义步长,用来表示每次滑多长。这样我们就能每次向下走一点点,再定义一个迭代值用来表示滑多少次,这样我们就能慢慢的一点点的靠近最小值了,不出意外还是能距离最优值很近的。
具体实现如下:
每次向下滑要慢慢滑,就是要个步长,我们定义为learning_rate,往往很小的一个值。
向下滑动的次数,就是迭代的次数,我定义为num_iter,相对learning_rate往往很大。
定义好这两个,我们就可以一边求梯度,一边向下滑了。就是去更新a和b。
b=b+learning_rate∗∂J(θ)∂bb=b+learning\_rate*\frac{\partial J(\theta)}{\partial b}b=b+learning_rate∗∂b∂J(θ)
a=a+learning_rate∗∂J(θ)∂aa=a+learning\_rate*\frac{\partial J(\theta)}{\partial a}a=a+learning_rate∗∂a∂J(θ)
对于上面的例2,如下图所示,过程如下:
#step 1 get train data
res=[]
with open('d:/shuju1.txt','r') as f:
lines=f.readlines()
for line in lines:
res.append(list(map(float,line.strip('\n').split(','))))
res=np.array(res)
data=res
#step 2 define hyperparamters
#learning_rate is used to update gradient
#define the number that will iterate
#define y=a+bx
learning_rate=0.001
initial_b=0
initial_a=0
num_iter=1000
#step 3 optimize
[a,b]=optimizer(data,initial_a,initial_b,learning_rate,num_iter)
结果为:
(0.24852432182905326, 0.7411262595522877)
以下是用到的优化器函数,优化器就是去做梯度下降:
def optimizer(data,init_a,init_b,learning_rate,num_iter):
b=init_b
a=init_a
#gradient descent
for i in range(num_iter):
a,b=compute_gradient(a,b,data,learning_rate)
#if i%100==0:
#print('iter{0}:error={1}'.format(i,computer_error(a,b,data)))
return [a,b]
里面的compute_gradient方法就是去计算梯度做参数更新.
def compute_gradient(a_current,b_current,data,learning_rate):
a_gradient=0
b_gradient=0
M=float(len(data))
for i in range(len(data)):
x=data[i,0]
y=data[i,1]
a_gradient+= -(1/M)*(y-(a_current+b_current*x))
b_gradient+= -(1/M)*x*(y-(a_current+b_current*x))
new_b=b_current-(learning_rate*b_gradient)
new_a=a_current-(learning_rate*a_gradient)
return [new_a,new_b]
3.2 局部加权线性回归
给待测点附近的每个点赋予一定的权重。
损失函数为:J(θ)=12M∑i=1mωi(yi−(a+bxi))2J(\theta)=\frac{1}{2M}\sum\limits_{i=1}^m\omega_i(y_i-(a+bx_i))^2J(θ)=2M1i=1∑mωi(yi−(a+bxi))2,其中,ωi\omega_iωi表示第i个样本的权重。
局部加权线性回归使用”核“来对附近的点赋予更高的权重。核的类型可以自由选择,最常用的核就是高斯核,高斯核对应的权重如下:
ωi=exp(∣xi−x∣−2k2)\omega_i=exp(\frac{|x_i-x|}{-2k^2})ωi=exp(−2k2∣xi−x∣)
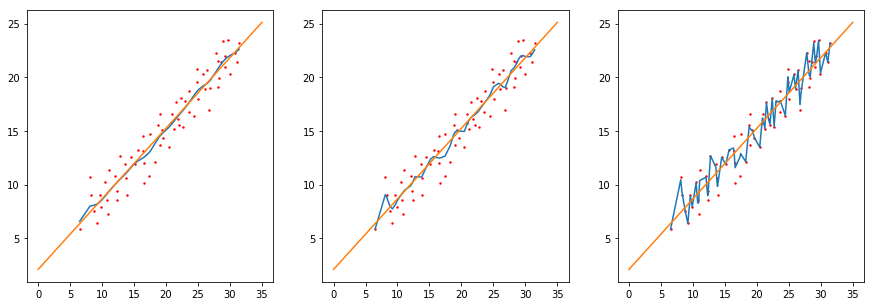
这样就有一个只含对角元素的权重矩阵W, 并且点xix_ixi与x 越近,ωi\omega_iωi也会越大。这里的参数k 决定了对附近的点赋予多大的权重,这也是唯一需要考虑的参数。
当k越大,有越多的点被用于训练回归模型;
当k越小,有越少的点用于训练回归模型。
下面给出局部加权线性回归的推导过程.这里,我们换一种写法.
目标函数定义为:hθ(x)=θ0+θ1x1=θ0x0+θ1x1=∑i=0mθixi=θTxh_{\theta}(x)=\theta_0+\theta_1x_1=\theta_0x_0+\theta_1x_1=\sum\limits_{i=0}^m\theta_ix_i=\theta^Txhθ(x)=θ0+θ1x1=θ0x0+θ1x1=i=0∑mθixi=θTx,这里设x0=1x_0=1x0=1.
我们的目标是最小化cost function:
J(θ)=12M∑i=1mω(i)[hθ(x(i)−y(i)]2=12M(Xθ−Y)TW(Xθ−Y)J(\theta)=\frac{1}{2M}\sum\limits_{i=1}^m\omega^{(i)}[h_{\theta}(x^{(i)}-y^{(i)}]^2=\frac{1}{2M}(X\theta-Y)^TW(X\theta-Y)J(θ)=2M1i=1∑mω(i)[hθ(x(i)−y(i)]2=2M1(Xθ−Y)TW(Xθ−Y),
这里,我们省略J(θ)J(\theta)J(θ)中的系数12M\frac{1}{2M}2M1.我们的目标是min0∑i=1mω(i)[hθ(x(i))−y(i)]2\underset{0}{min}\sum\limits_{i=1}^m\omega^{(i)}[h_{\theta}(x^{(i)})-y^{(i)}]^20mini=1∑mω(i)[hθ(x(i))−y(i)]2.
换成线性代数的表述方式:∑i=1mω(i)[hθ(x(i))−y(i)]2=(Xθ−Y)TW(Xθ−Y)\sum\limits_{i=1}^m\omega^{(i)}[h_{\theta}(x^{(i)})-y^{(i)}]^2=(X\theta-Y)^TW(X\theta-Y)i=1∑mω(i)[hθ(x(i))−y(i)]2=(Xθ−Y)TW(Xθ−Y),其中
$
W=\begin{bmatrix}
w^{(1)} & 0 & 0\
0 & w^{(2)} & 0\
\vdots & \ddots & \vdots\
0 & 0 & w^{(m)}\
\end{bmatrix}
$
是mxm维的对角矩阵,
$
X=\begin{bmatrix}
1 & x_1^{(1)} & \cdots & x_{n-1}^{(1)} \
1 & x_1^{(2)} & \cdots & x_{n-1}^{(2)} \
\vdots & \vdots & \ddots & \vdots \
1 & x_1^{(m)} & \cdots & x_{n-1}^{(m)}\
\end{bmatrix}是mxn维的输入矩阵,
$
,$
Y=\begin{bmatrix}
y{(1)}\y{(2)}\ \vdots \ y^{(m)}\
\end{bmatrix}
$是mx1维的结果,
θ=[θ0θ1]\theta=\begin{bmatrix}\theta_0 \\ \theta_1 \\ \end{bmatrix}θ=[θ0θ1]是nx1维的参数向量.
下面对J(θ)J(\theta)J(θ)求偏导.
$
\begin{array}{lll}
\frac{\partial}{\partial \theta}J(\theta)&=&\frac{\partial}{\partial \theta}(X\theta-Y)^TW(X\theta-Y)\
&=&\frac{\partial}{\partial \theta}(\thetaTXTWX\theta-\thetaTXTWY-YTWX\theta+YTWY)\
&=&(XTWX\theta-XTWY)
\end{array}
$,
令∂∂θJ(θ)=0\frac{\partial}{\partial \theta}J(\theta)=0∂θ∂J(θ)=0,有(XTWXθ−XTWY)=0(X^TWX\theta-X^TWY)=0(XTWXθ−XTWY)=0,即θ=(XTWX)−1XTWY\theta=(X^TWX)^{-1}X^TWYθ=(XTWX)−1XTWY.
上面的例2,代码如下:
首先获取数据如下:
import numpy as np
res=[]
with open('d:/shuju1.txt','r') as f:
lines=f.readlines()
for line in lines:
res.append(list(map(float,line.strip('\n').split(','))))
res=np.array(res)
t=np.matrix([[1]*67])
X=np.hstack((t.T.A,np.matrix(res[:,0]).T.A))
X=np.matrix(X)
Y=np.matrix(res[:,1]).T.A
Y=np.matrix(Y)
其次,相关的函数如下:
import copy
def lwlr(testPoint,xArr,yArr,k=1.0):
xMat = np.mat(xArr); yMat = np.mat(yArr)
m = np.shape(xMat)[0]
weights = np.mat(np.eye((m)))
for j in range(m): #next 2 lines create weights matrix
diffMat = testPoint - xMat[j,:] #
weights[j,j] = np.exp(diffMat*diffMat.T/(-2.0*k**2))
xTx = xMat.T * (weights * xMat)
if np.linalg.det(xTx) == 0.0:
print("This matrix is singular, cannot do inverse")
return
ws = xTx.I * (xMat.T * (weights * yMat))
return testPoint * ws
def lwlrTest(testArr,xArr,yArr,k=1.0): #loops over all the data points and applies lwlr to each one
test=copy.copy(testArr)
m = np.shape(testArr)[0]
yHat = np.zeros(m)
for i in range(m):
yHat[i] = lwlr(test[i],xArr,yArr,k)
return yHat
如果要画出图形的话,首先要将数据X排序,然后求出对应的预测值,再画出图像.
def lwlrTestPlot(xArr,yArr,k=1.0): #same thing as lwlrTest except it sorts X first
yHat = np.zeros(np.shape(yArr)) #easier for plotting
xCopy = copy.copy(np.mat(xArr))
xCopy.sort(0)
for i in range(np.shape(xArr)[0]):
yHat[i] = lwlr(xCopy[i],xArr,yArr,k)
return yHat,xCopy
#画图代码如下
import matplotlib.pyplot as plt
fig=plt.figure(figsize=(15,5))
xs=[1,0.5,0.1]
for i in range(3):
y1,x1=lwlrTestPlot(X[:,1],Y,xs[i])
n="ax"+str(i)
pj=131+i;i+=1
n=fig.add_subplot(pj)
n.plot(x1,y1)
n.scatter(X[:,1].flatten().A[0],Y.flatten().A[0],s=2,c='red')
a=2.10892056;b=0.65771558
x=np.linspace(0,35,100)
y=a+b*x
n.plot(x,y)
plt.show()
附录
设总体均值为μ\muμ,总体方差为σ\sigmaσ,样本均值为xˉ=1n∑i=1nxi\bar{x}=\frac{1}{n}\sum\limits_{i=1}^nx_ixˉ=n1i=1∑nxi,则样本方差var(x)=S2var(x)=S^2var(x)=S2为:
var(x)=S2=1n−1∑i=1n(xi−xˉ)2var(x)=S^2=\frac{1}{n-1}\sum\limits_{i=1}^n(x_i-\bar{x})^2var(x)=S2=n−11i=1∑n(xi−xˉ)2,这里分母为n-1是因为:
E(1n∑i=1n(xi−xˉ)2)=1nE(∑i=1n(xi2−2xixˉ+xˉ2))E(\frac{1}{n}\sum\limits_{i=1}^n(x_i-\bar{x})^2)=\frac{1}{n}E(\sum\limits_{i=1}^n(x_i^2-2x_i\bar{x}+\bar{x}^2))E(n1i=1∑n(xi−xˉ)2)=n1E(i=1∑n(xi2−2xixˉ+xˉ2))
=1nE(∑i=1nxi2−2∑i=1nxixˉ+∑i=1nxˉ2)=1n(E∑i=1nxi2−2E∑i=1nxixˉ+nExˉ2)=\frac{1}{n}E(\sum\limits_{i=1}^nx_i^2-2\sum\limits_{i=1}^nx_i\bar{x}+\sum\limits_{i=1}^n\bar{x}^2)=\frac{1}{n}(E\sum\limits_{i=1}^nx_i^2-2E\sum\limits_{i=1}^nx_i\bar{x}+nE\bar{x}^2)=n1E(i=1∑nxi2−2i=1∑nxixˉ+i=1∑nxˉ2)=n1(Ei=1∑nxi2−2Ei=1∑nxixˉ+nExˉ2)
=1n(E∑i=1nxi2−2nExˉ2+n(Dxˉ+(Exˉ)2))=\frac{1}{n}(E\sum\limits_{i=1}^nx_i^2-2nE\bar{x}^2+n(D\bar{x}+(E\bar{x})^2))=n1(Ei=1∑nxi2−2nExˉ2+n(Dxˉ+(Exˉ)2))
=1n(∑i=1nExi2−2n(Dxˉ+(Exˉ)2)+n(Dxˉ+(Exˉ)2))=\frac{1}{n}(\sum\limits_{i=1}^nEx_i^2-2n(D\bar{x}+(E\bar{x})^2)+n(D\bar{x}+(E\bar{x})^2))=n1(i=1∑nExi2−2n(Dxˉ+(Exˉ)2)+n(Dxˉ+(Exˉ)2))
=1n(∑i=1nExi2−n(Dxˉ+(Exˉ)2))=1n(∑i=1n(Dxi+(Exi)2)−n(1nσ2+μ2))=\frac{1}{n}(\sum\limits_{i=1}^nEx_i^2-n(D\bar{x}+(E\bar{x})^2))=\frac{1}{n}(\sum\limits_{i=1}^n(Dx_i+(Ex_i)^2)-n(\frac{1}{n}\sigma^2+\mu^2))=n1(i=1∑nExi2−n(Dxˉ+(Exˉ)2))=n1(i=1∑n(Dxi+(Exi)2)−n(n1σ2+μ2))
1n(n(σ2+μ2)−σ2−nμ2)=1n(n−1)σ2=n−1nσ2\frac{1}{n}(n(\sigma^2+\mu^2)-\sigma^2-n\mu^2)=\frac{1}{n}(n-1)\sigma^2=\frac{n-1}{n}\sigma^2n1(n(σ2+μ2)−σ2−nμ2)=n1(n−1)σ2=nn−1σ2,
而定义S2=1n−1∑i=1n(xi−xˉ)2S^2=\frac{1}{n-1}\sum\limits_{i=1}^n(x_i-\bar{x})^2S2=n−11i=1∑n(xi−xˉ)2,则由上面的计算知道ES2=σ2ES^2=\sigma^2ES2=σ2,即S2S^2S2是σ2\sigma^2σ2的无偏估计.
同理,样本协方差定义为
cov(x,y)=∑i=1n(xi−xˉ)(yi−yˉ)n−1cov(x,y)=\frac{\sum\limits_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{n-1}cov(x,y)=n−1i=1∑n(xi−xˉ)(yi−yˉ),var(x)=1n−1∑i=1n(xi−xˉ)2var(x)=\frac{1}{n-1}\sum\limits_{i=1}^n(x_i-\bar{x})^2var(x)=n−11i=1∑n(xi−xˉ)2.





 本文深入解析一元线性回归模型,涵盖基础原理、数学推导及R语言实践,探讨最小二乘法求解参数,梯度下降法及局部加权线性回归的应用。
本文深入解析一元线性回归模型,涵盖基础原理、数学推导及R语言实践,探讨最小二乘法求解参数,梯度下降法及局部加权线性回归的应用。
















 5289
5289

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








