在学习了栈和队列的基本实现后,我们依次学习二者在实际问题中的应用。都是最典型的应用,基本以LeetCode的题目为例。由于栈的后进先出的特点,栈的应用主要有括号匹配、后缀表达式计算、数制转换等。
应用1:括号匹配
LeetCode 20. Valid Parentheses(有效的括号)
Given a string containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.
An input string is valid if:
Open brackets must be closed by the same type of brackets.
Open brackets must be closed in the correct order.
Note that an empty string is also considered valid.
题目解析:
遍历字符串,考察每一个字符c。如果c为左括号,记录下来,希望c能够与后面出现的同类型最近右括号匹配。如果c为右括号,考察它能否与缓冲区中的(前一个)左括号匹配。这个匹配过程,明显是后进先出——栈。
class Solution:
def isValid(self, s):
"""
:type s: str
:rtype: bool
"""
stack = []
for ch in s:
if ch in ['(','[','{']:
stack.append(ch)
else:
if stack:
left = stack.pop()
else:
return False
if left=='[' and ch ==']' or left=='(' and ch==')' or left=='{' and ch=='}':
continue
else:
return False
if stack == []:
return True
else:
return False
具体解释看下面其他人讲解的:

举一反三:最长括号匹配
给定字符串,可能不是完全匹配的,要求你找出最长的匹配的括号子串,返回其长度。可以简化为只包含‘(’、‘)’的问题尝试一下。
其基本思想仍然是栈,算法思想如下:
初始位置 p = -1(-1方便计算长度),manlen=0 ,遍历字符串,对于第i位字符c,如果c为左括号,压栈(由于都是左圆括号,我们将位置i压栈);如果c为右括号,它一定与栈顶(如果栈不空)左括号匹配;
如果栈为空,以此为分界,该位置左边处理完毕(即后边再有匹配的长度也不叠加),将p设置为i;
如果栈不空,出栈一个元素。出栈后栈空,i-p为当前匹配成功的长度;栈仍不空,栈顶的元素记录上一次的位置t,i-t是当前匹配成功的长度。当然有最大的长度的话更新 maxlen 。
此题不再贴代码,可自行尝试。
应用2:后缀表达式
150. Evaluate Reverse Polish Notation(计算逆波兰表达式RPN)
Evaluate the value of an arithmetic expression in Reverse Polish Notation.
Valid operators are +, -, *, /. Each operand may be an integer or another expression.
Some examples:
["2", "1", "+", "3", "*"] -> ((2 + 1) * 3) -> 9
["4", "13", "5", "/", "+"] -> (4 + (13 / 5)) -> 6
题目解析:
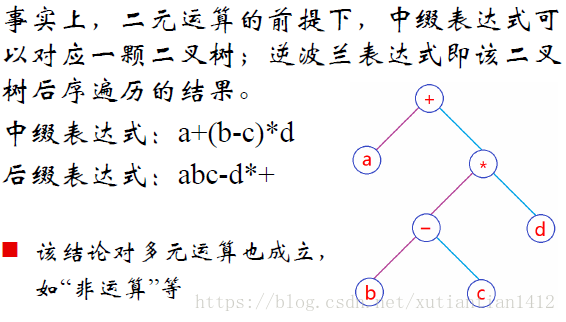
后缀表达式的计算是栈的重要应用,看下面的图理解一下运算符与二叉树的关系,因此栈与二叉树的遍历也是息息相关(后面学习树的时候还会用到)。问题不难,代码贴出如下:
class Solution:
def evalRPN(self, tokens):
"""
:type tokens: List[str]
:rtype: int
"""
stack = []
for s in tokens:
if s in ['+','-','*','/']:
b = stack.pop()
a = stack.pop()
if s == '+':
stack.append(a+b)
elif s == '-':
stack.append(a-b)
elif s == '*':
stack.append(a*b)
else:
stack.append(int(a/b))
else:
stack.append(int(s))
ans = int(stack.pop())
return ans
后缀表达式在计算机中应用十分方便,是不需要带括号的优先级的。
应用3:数值转换
数制转换问题其实不用栈也可解决,但其实基本思想仍然是后进先出,看下面这个例子:
(2007)10 = (3727)8,十进制2007转换为八进制。
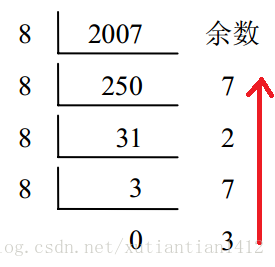
可以看出,余数转换成最后的数字是自下向上的,这就是栈的基本特点。在此不举例子了,实在是图森破了。
下面一篇继续关注于栈的leetcode的题目,欢迎阅读~
 栈的应用实例
栈的应用实例










 本文通过LeetCode题目详细介绍了栈在括号匹配、后缀表达式计算及数制转换等问题中的应用。并通过具体示例展示了如何利用栈高效解决问题。
本文通过LeetCode题目详细介绍了栈在括号匹配、后缀表达式计算及数制转换等问题中的应用。并通过具体示例展示了如何利用栈高效解决问题。
















 2213
2213

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








