洛谷P1518 [USACO2.4]两只塔姆沃斯牛 The Tamworth Two

洛谷P1518 [USACO2.4]两只塔姆沃斯牛 The Tamworth Two

• 标签：简单模拟
• 难度：简单+（普及/提高-）

题目描述

两只牛逃跑到了森林里。Farmer John 开始用他的专家技术追捕这两头牛。你的任务是模拟他们的行为（牛和 John）。

追击在10×10 的平面网格内进行。一个格子可以是：一个障碍物，两头牛（它们总在一起），或者 Farmer John。两头牛和 Farmer John 可以在同一个格子内（当他们相遇时），但是他们都不能进入有障碍的格子。

一个格子可以是：

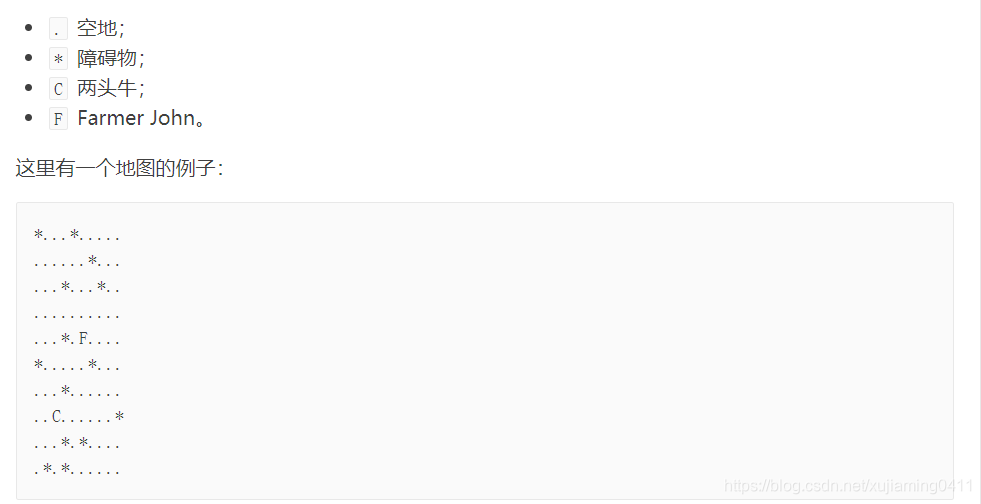
牛在地图里以固定的方式游荡。每分钟，它们可以向前移动或是转弯。如果前方无障碍（地图边沿也是障碍），它们会按照原来的方向前进一步。否则它们会用这一分钟顺时针转 90 度。 同时，它们不会离开地图。

Farmer John 深知牛的移动方法，他也这么移动。

每次（每分钟）Farmer John 和两头牛的移动是同时的。如果他们在移动的时候穿过对方，但是没有在同一格相遇，我们不认为他们相遇了。当他们在某分钟末在某格子相遇，那么追捕结束。

读入十行表示地图。每行都只包含 10 个字符，表示的含义和上面所说的相同。保证地图中只有一个 F 和一个 C。F 和 C 一开始不会处于同一个格子中。

计算 Farmer John 需要多少分钟来抓住他的牛，假设牛和 Farmer John 一开始的行动方向都是正北（即上）。 如果 John 和牛永远不会相遇，输出 0。

输入格式

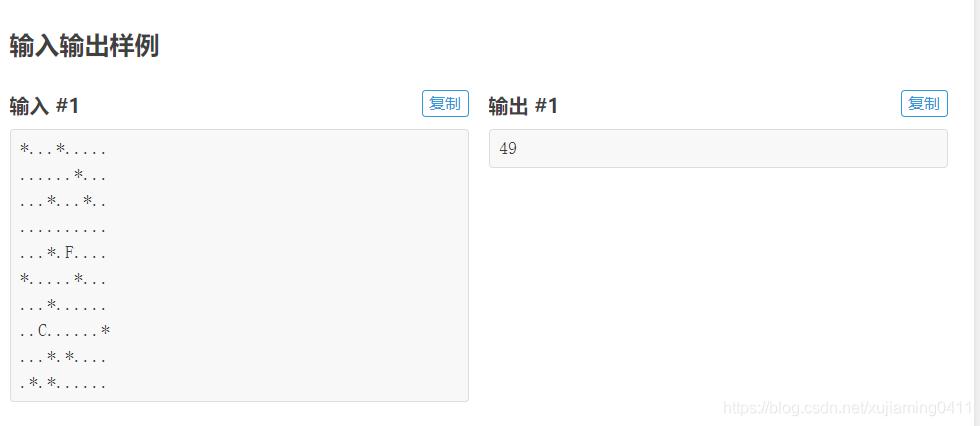
输入共十行，每行 10 个字符，表示如上文描述的地图。

输出格式

输出一个数字，表示 John 需要多少时间才能抓住牛们。如果 John 无法抓住牛，则输出 0。

题目分析

这题程序主题是不难的，可以按照题意模拟递归下去，主要值得思考的是：什么时候什么条件可以判定牛和John永远不可能相遇？

如果想让牛和John不相遇，因为只要时间足够长，他们的路径必定是确定的，然后不断地在这个路径上循环，让他们不相遇，即就是要求这两条路径没有交点。那么只要考虑一个周期（即一个循环里面两者是否相遇足矣）。
那么又如何判断一个周期的结束与停止呢？
这里并不需要多么准确的判断，只需要给出必要条件即可。
对于牛当前所处的点A以及John当前所处的点B，若（A,B）这个组合在牛和John之前的运动过程中已经出现了4次，这是第5次出现，则必然这5次中有两次的状态是一样的（即位置一样，下一步的方向一样）所以必然已经进入了循环状态（或许之前很早就进入了，或许这一步才进入），这个时候两者却还未相遇，那么之后两者必然不会相遇。

代码附

#include<bits/stdc++.h>
using namespace std;
int cowx,cowy,farx,fary,vis[12][12][12][12]={0};
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
// 用数字记录方向，改变方向直接数字加一后对4取模。
char ch[15][15];
void work(int step,int fdir,int cdir)
{
	if(cowx == farx && fary == cowy)
	{
		cout<<step;
	}
	else
	{
		vis[farx][fary][cowx][cowy]++;
		if(vis[farx][fary][cowx][cowy] > 4)
		{
			cout<<0; 
			// 判断是否进入循环，进入则结束退出。
		}
		else
		{
			if(ch[farx+dx[fdir]][fary+dy[fdir]]!='*')
			{
				farx+=dx[fdir];
				fary+=dy[fdir];
			}
			else
			{
				fdir = (fdir+1)%4;
			}
			if(ch[cowx+dx[cdir]][cowy+dy[cdir]]!='*')
			{
				cowx+=dx[cdir];
				cowy+=dy[cdir];
			}
			else
			{
				cdir = (cdir+1)%4;
			}
			// fdir:John的方向参数
			// cdir:牛的方向参数
			work(step+1,fdir,cdir);
		}
	}
}
int main()
{
	for(int i = 1; i <= 10;i++)
	{
		for(int j = 1; j <= 10; j++)
		{
			cin>>ch[i][j];
			if(ch[i][j]=='F') 
			{
				farx = i;
				fary = j;
				ch[i][j]='.';
			}
			if(ch[i][j]=='C')
			{
				cowx = i;
				cowy = j;
				ch[i][j]='.';
			}
		}
		
	}
	for(int i = 1; i <= 10; i++)
	{
		ch[0][i] = '*';
		ch[i][0] = '*';
		ch[11][i] = '*';
		ch[i][11] = '*';
	}//将边界设置为障碍
	work(0,0,0);
	return 0;
}