数据结构与算法学习笔记（六）插入、希尔、归并排序

1. 插入排序

1.1 概述

插入排序，一般也被称为直接插入排序。它的基本思想是将一个记录插入到已经排好序的有序表中，从而一个新的、记录数增1的有序表。

在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动。

1.2 基本原理

(一). 定义一个数组

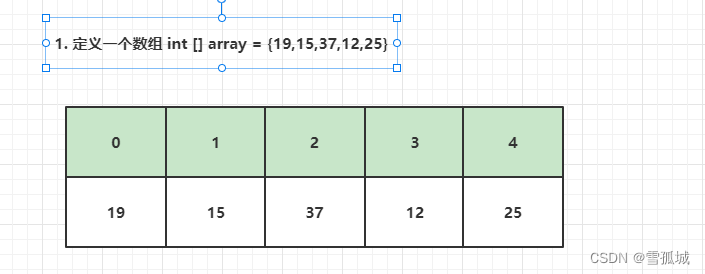
(二). 第一次循环

(三). 第二次循环

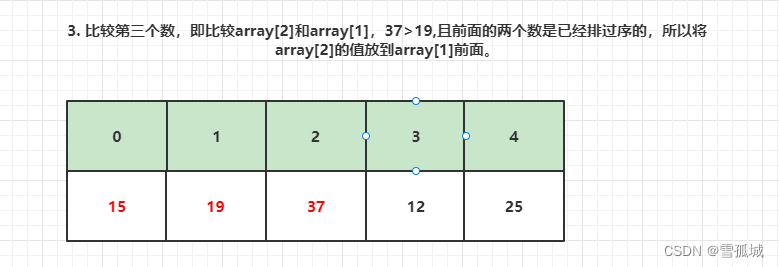
(三). 第三次循环

比较逻辑代码：

if (array[i] < array[i - 1]){
	int temp = array[i];
	array[i] = array[i - 1];
}

填充完array[3]后，我们需要将下标向前移动一个位置，好将temp（原来的array[3]）跟array[1]进行比较，但是此时下标 i 代表着循环的位置不能移动。因此，我们需要再定义一个变量 j 来记录比较的位置，因此将上述代码优化成如下：

// 当array[i] < array[i-1]时才需要处理
if (array[i] < array[i-1]){
	int temp = array[i];
	int j = i;
	// 将比temp大的数往后挪一个位置，为temp腾出一个合适位置
	while(j > 0 && temp < array[j - 1]){
		array[j] = array[j - 1];
		// 填充完后, 继续向前比较
		j--;
	}
}

此时 j 移动到下标2，比较temp和array[1]，即12和19。因为12 < 19，并且原来array[2]位置的数37此时已经填入array[3]，因此此时array[2]相当于一个坑，直接将19填入即可。

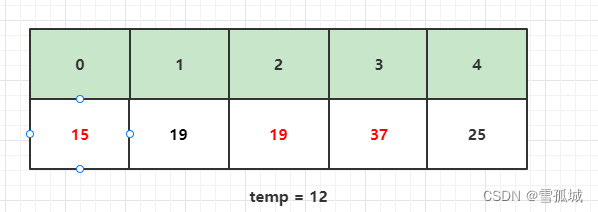
填完后，将下标 j 继续向前移动一个位置。

此时 j 移动到下标1，此时比较temp和array[0]，即12和15。因为12 < 15，并且原来array[1]位置的数19此时已经填入array[2]，因此直接将15填入array[1]，此时array[0]又形成了一个新的坑。

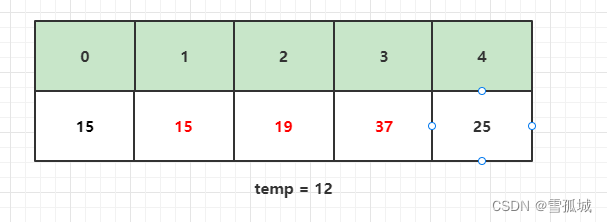
此时 j 移动到下标0，已经没有前面的数可以比较了。因此，array[0]即为temp的位置，将temp填入array[0]后结束此次循环。

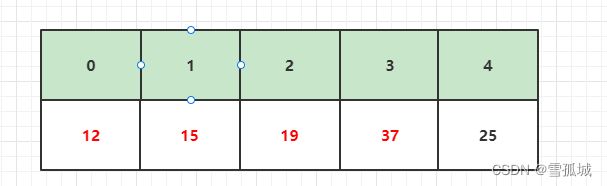
所以，此时的代码为：

// 当array[i] < array[i-1]时才需要处理
if (array[i] < array[i-1]){
	int temp = array[i];
	int j = i;
	// 将比temp大的数往后挪一个位置，为temp腾出一个合适位置
	while(j > 0 && temp < array[j - 1]){
		array[j] = array[j - 1];
		// 填充完后, 继续向前比较
		j--;
	}
	// 放置temp的位置
	array[j] = temp;
}

(四). 第四次循环

比较第五个数，即比较array[4]和array[3]，因为25 < 37，所以将25赋值给temp，并将37填入array[4]的位置，并将下标 j 向前移动一个位置。

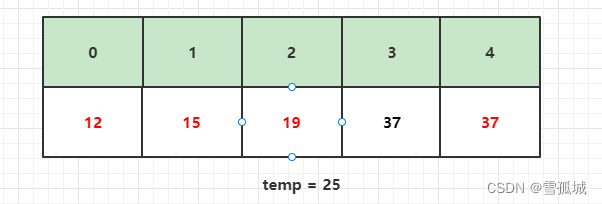
此时 j 移动到下标3，此时比较temp和array[2]，即25和19。因为25 > 19，所以array[3]即为25的位置，将25填入array[3]后结束此次循环，至此，整个排序过程结束。

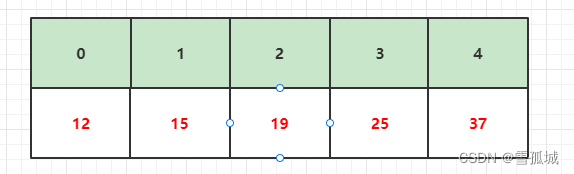
1.3 代码逻辑

    // 插入排序
    public static void insertionSort(int[] array){
        if (array == null || array.length == 0){
            return;
        }
        for (int i = 1; i < array.length; i++){
            // 当array[i] < array[i-1]时才需要处理
            if (array[i] < array[i-1]){
                int temp = array[i];
                int j = i;
                // 将比temp大的数往后挪一个位置，为temp腾出一个合适位置
                while(j > 0 && temp < array[j - 1]){
                    array[j] = array[j - 1];
                    // 填充完后, 继续向前比较
                    j--;
                    System.out.println("此时数组状态为:" + Arrays.toString(array));
                }
                // 放置temp的位置
                array[j] = temp;
            }
        }
    }

1.4 时间&空间复杂度

• 在最坏的情况下，即整个数组是倒序的，比较次数 = 1 + 2 + 3 + … + (n - 2) + (n - 1) = n * (n - 1) / 2，此时的时间复杂度为：O(n^2)。
• 在最好的情况下，即整个数组是正序的，比较次数 = n - 1，此时的时间复杂度为：O(n)。
• 插入排序的空间复杂度为常数阶：O(1)。

2. 希尔排序

2.1 概述

希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

2.2 基本原理

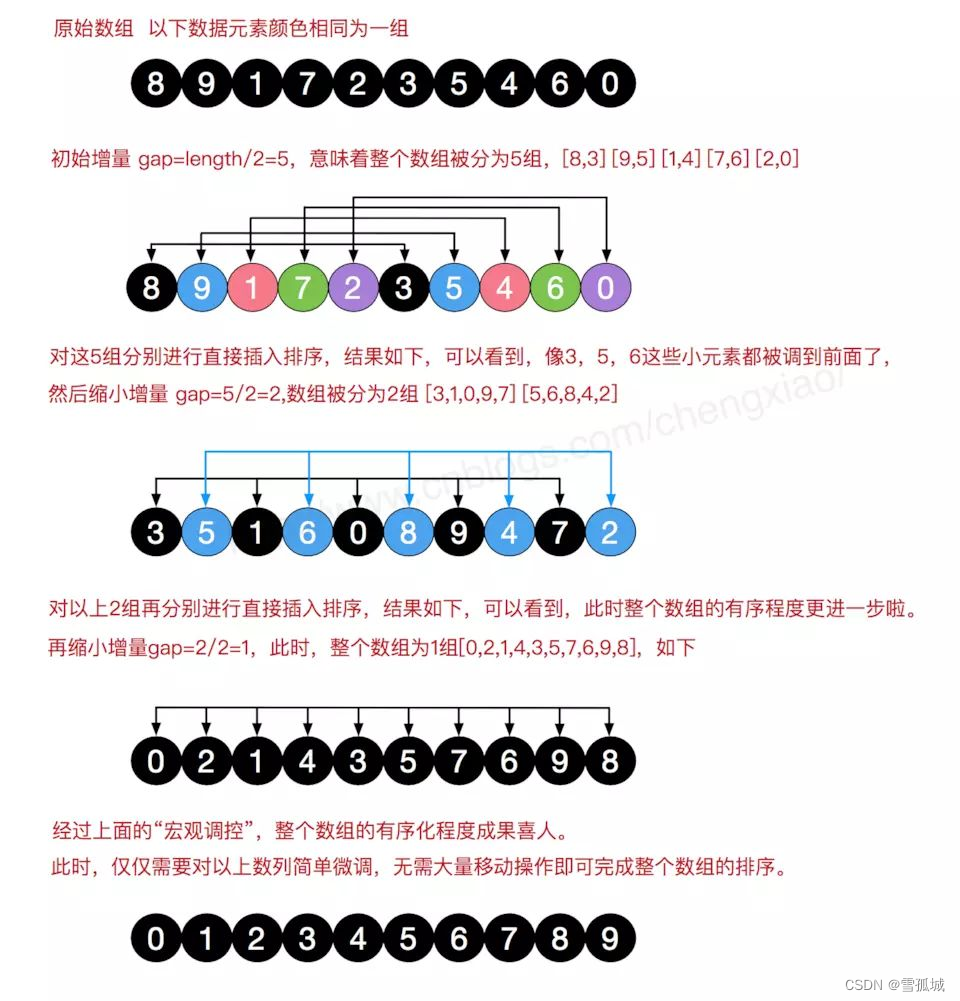
2.3 代码逻辑

    // 希尔排序
    public static void shellSort(int[] array) {
        // 增量每次/2
        for (int step = array.length / 2; step > 0; step = step / 2){
            // 从增量那组开始进行插入排序，直至完毕
            for (int i = step; i < array.length; i++){
                int j = i;
                int temp = array[j];
                // j - step 就是代表与它同组隔壁的元素
                while (j - step >= 0 && array[j - step] > temp){
                    array[j] = array[j - step];
                    j = j - step;
                }
                array[j] = temp;
                System.out.println("此时数组状态为:" + Arrays.toString(array));
            }
        }
    }

2.4 时间&空间复杂度

• 时间复杂度：O(n^2/3)
• 空间复杂度：O(1)

3. 归并排序

3.1 概述

归并排序是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

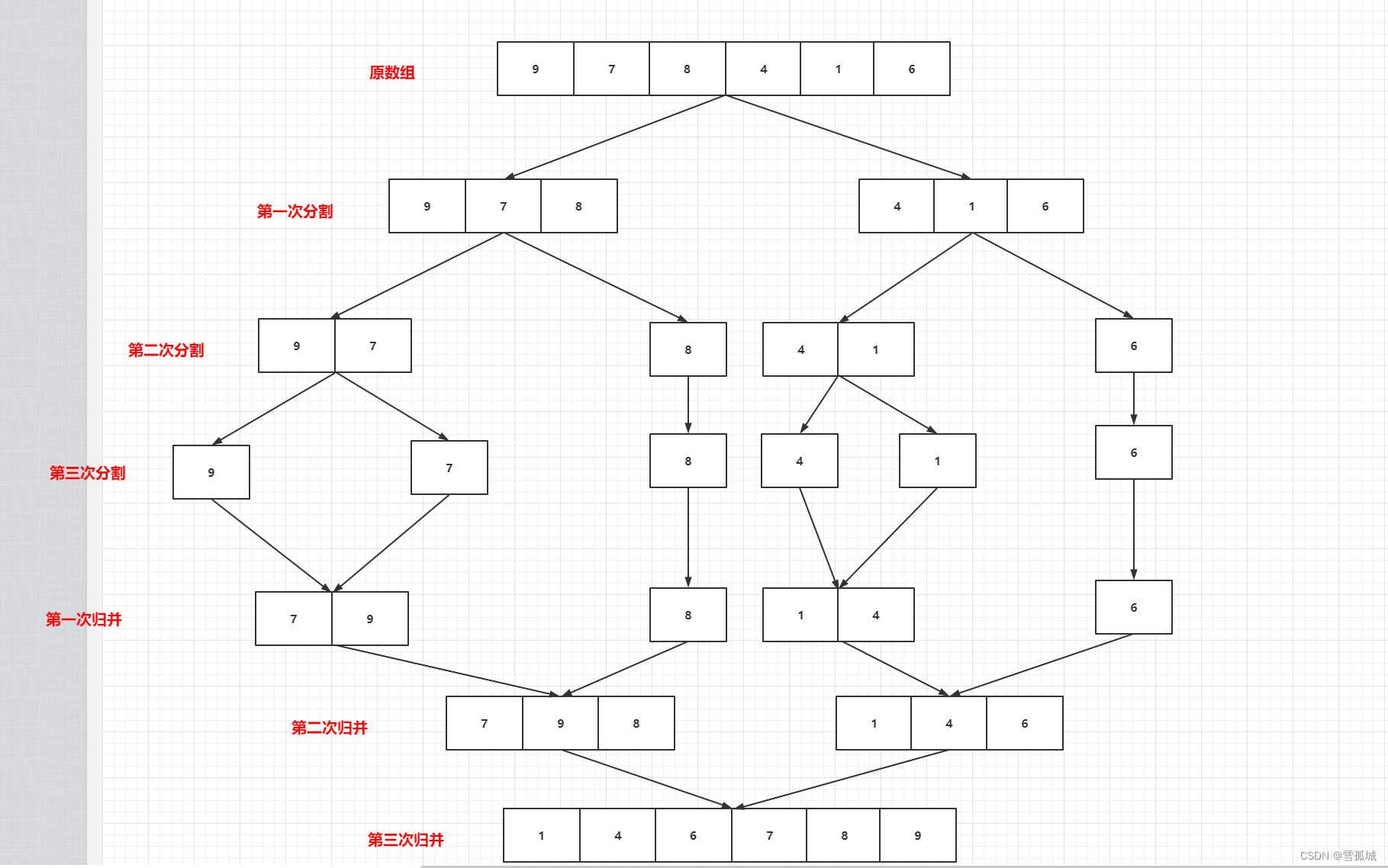
3.2 基本原理

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
4. 重复步骤3直到某一指针超出序列尾
5. 将另一序列剩下的所有元素直接复制到合并序列尾

3.1 代码逻辑

	// 归并排序
    public static void mergeSort(int[] array,int left,int right){
        if (left >= right){
            return ;
        }
        int mid = (left + right) / 2;
        // 左有序数组
        mergeSort(array,left,mid);
        // 右有序数组
        mergeSort(array,mid + 1,right);
        
        merge(array,left,mid,right);
    }

	public static void merge(int[] array,int left,int mid,int right){
        // 根据拿到的左边界，定其为第一个数组的指针
        int s1 = left;
        // 根据中间位置，让中间位置右移一个单位，那就是第二个数组的指针
        int s2 = mid + 1;
        // 根据左右边界相减得到这片空间的长度，以此声明额外空间
        int[] temp = new int[right - left + 1];
        // 定义额外空间的指针
        int i = 0;
        while (s1 <= mid && s2 <= right){
            // 如果第一个数组的指针数值小于第二个数组的，那么其放置在临时空间上
            if (array[s1] <= array[s2]){
                temp[i++] = array[s1++];
            }else {
                temp[i++] = array[s2++];
            }
        }
        // 如果这是s1仍然没有到达其终点，那么说明它还有剩
        while (s1 <= mid){
            // 每个参与合并的数组都是有序数组，因此直接往后拼接即可
            temp[i++] = array[s1++];
        }
        while (s2 <= right){
            temp[i++] = array[s2++];
        }
        //数组复制
        for (int j = 0; j < temp.length; j++){
            array[j + left] = temp[j];
        }
    }

3.1 时间&空间复杂度

• 时间复杂度：O(n㏒n)
• 空间复杂度：O(N)