如何让小白写出归并排序求逆序对

昨日和小白们分享了一个归并排序求逆序对的算法思想，对于此算法的学习，一般小白学不明白。包括曾经的小白的我，理解这个算法可是费了老大劲了。那么我希望我的小白们能学起来轻松且水到渠成些。所以，在此记录下，供以后用。（当然以后还用得到么，我也不清楚，据说自招的改革会让很多二三流学校的孩子们学不下去的，以后我可能退役了）。
　　【学情分析】已具备对递归函数的执行过程的理解，而且对分析递归能解决的问题，基本会从两个方面去思考如何写递归：递归边界和递归式。
　　【分享过程】
　　１.写了一个简短的程序分析递归函数调用之前的代码和递归之后写的代码对程序结果的影响。
程序一：

#include<bits/stdc++.h>
using namespace std;
void fun(int n){
	if(n <= 0) return;
	cout << n << endl;
	fun(n-1);
}
int main(){
	fun(5);
	reuturn 0;
}

程序二

#include<bits/stdc++.h>
using namespace std;
void fun(int n){
	if(n <= 0) return;	
	fun(n-1);
	cout << n << endl;
}
int main(){
	fun(5);
	reuturn 0;
}

程序一的输出是在每次递归调用下一个函数之前输出，是在进入一次新的递归前做的事。
　　程序二的输出是在每次递归调用回来之后再进行输出，是在递归回来后做的事。
　　从以上两个程序帮助理解递归过程中要做的事的先后在程序表达时该放置的位置。
２.尝试分析解决问题二路归并排序问题。
　　给定两个非降的数字序列，要求合并后依然是非降的数字序列。其中每个序列的个数是3000000的样子，每个数值在-10⁹~10⁹之间，从这个数据量来看，将数据加入到一个数组中，在sort一遍，nlogn的时间复杂度会比较高，面临超时的危险；根据每个数值的范围来看，桶排序不现实。那么需要尝试O（n）的时间复杂度的方案。
抓住给定的两个有序序列的有序这个关键点，我们可以二路归并来解决。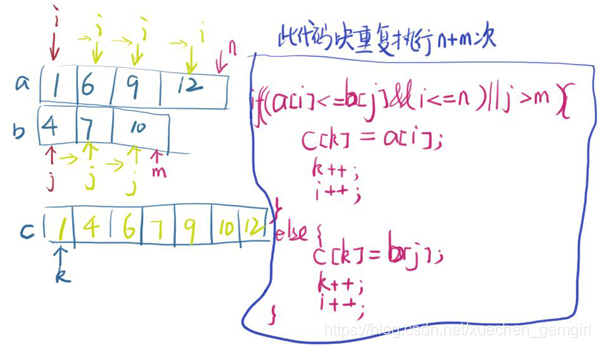给予大约40分钟左右的时间写出代码并AC

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 3000000+1;
int a[MAXN],b[MAXN],c[MAXN*2];
int main(){
	int n,m;
	cin >> n >> m;
	for(int i = 1;i<= n; i++)scanf("%d",&a[i]);
	for(int i = 1;i<= m; i++)scanf("%d",&b[i]);
	for(int k= 1,i = 1,j = 1;k<= n + m; k++){
		if((a[i] <= b[j]&& i<= n)|| j > m ){
			c[k] = a[i];
			i++;
		}else{
			c[k] = b[j];
			j++;
		}
		printf("%d ",c[k]);
	}
	return 0;
}

3.分析逆序对问题。
　　在二路归并中，假设两个序列是并列一排放着，a数组在前，b数组在后在这样的序列中存在多少个逆序对呢？分析当放b[j]时，是因为a[i]比它大，才会轮到b[j]放入c[k]中的，那么目前a数组中从i ~n为下标的数就都是大于目前b[j]的，因此可以与其产生逆序对n-i+1对。依次下去，对于每个b[j]放入c数组时，都去统计目前能产生的逆序对个数，这样累计下来便是这个前后拼接后的数组所存在的逆序对的个数，同时也二路归并为有序的状态了。
　　但是不是每个数组给定时能左右两部分有序，因此也就不能如此操作。那么如何能创造条件让其有序并满足此条件，并进行逆序对计算呢？
　　假设需要求逆序对的数据是a[1]至a[n]，那么需要求解决a[1]~a[(1+n)/2]序列的有序状态和逆序对问题，及a[(1+n)/2]至a[n]序列的有序状态和逆序对问题。我们会发现在这个过程中，问题没有变化，但是问题的规模在缩小，对于这类问题，我们可以采用递归来写。当递归到只有一个数时就停止继续分，当左右只有一个数时便可以看做两个有序序列在合并了，因此在分完回来，就开始对目前的序列的两部分进行二路归并，并顺带统计逆序对个数。因此递归式是：

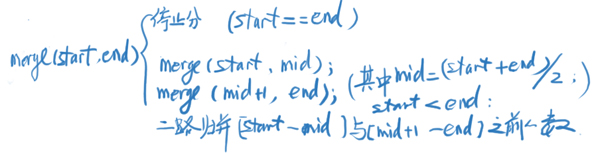
然后用一组数模拟分和合的过程。
　　其中蓝色笔记为在递归分的过程，红色笔记处为递归回来在做的并的过程。仔细观察为了原来的数组有序，在二路归并时有序的内容是被归并到一个辅助数组中的，因此在归并完后，需要再将辅助数组中的有序数值覆盖回原来数组对应的空间内。
　　详细见代码：

void mergesort(int left,int right){
	if(left == right) return;
	int mid = (left + right) / 2;
	mergesort(left, mid);    //分
	mergesort(mid+1 , right);//分
	// 二路归并
	int i = left,j = mid+1;
	for(int k = left ;k <= right; k++){
		if((a[i] <= a[j] && i<=mid) || j>right){
			tmp[k] = a[i];
			i++;
		} 
		else{
			ans += mid - i + 1;  //统计逆序对的个数。
			tmp[k] = a[j];
			j++;
		}
	} 
	for(int k = left; k <= right; k++){   //将辅助数组中的有序数值放回原始数组a中。
		a[k] = tmp[k];
	}
}

这样，就既排好了序，同时也统计了逆序对的数量。