梯度下降法求解多元线性回归 — NumPy

梯度下降法求解多元线性回归问题

使用梯度下降法求解一元线性回归的方法也可以被推广到求解多元线性回归问题。

这是多元线性回归的模型：

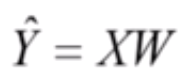
其中的 X 和 W 都是 m+1 维的向量。

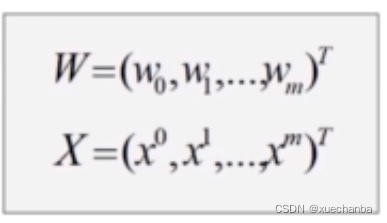
下图为它的损失函数：

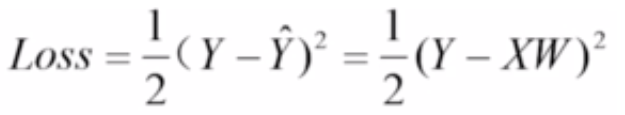
它也是一个高维空间中的凸函数，因此也可以使用梯度下降法来求解。
下图为它的权值更新算法：

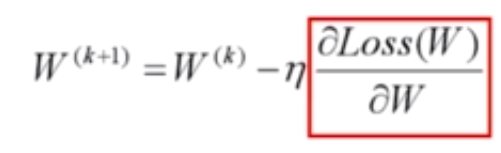
代入偏导数，

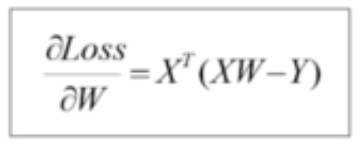
可以得到最终的迭代公式：

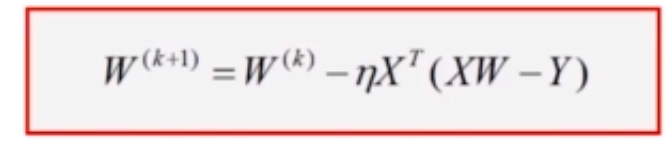
问题描述

依然是房价预测的问题，这是一个二元线性回归问题。

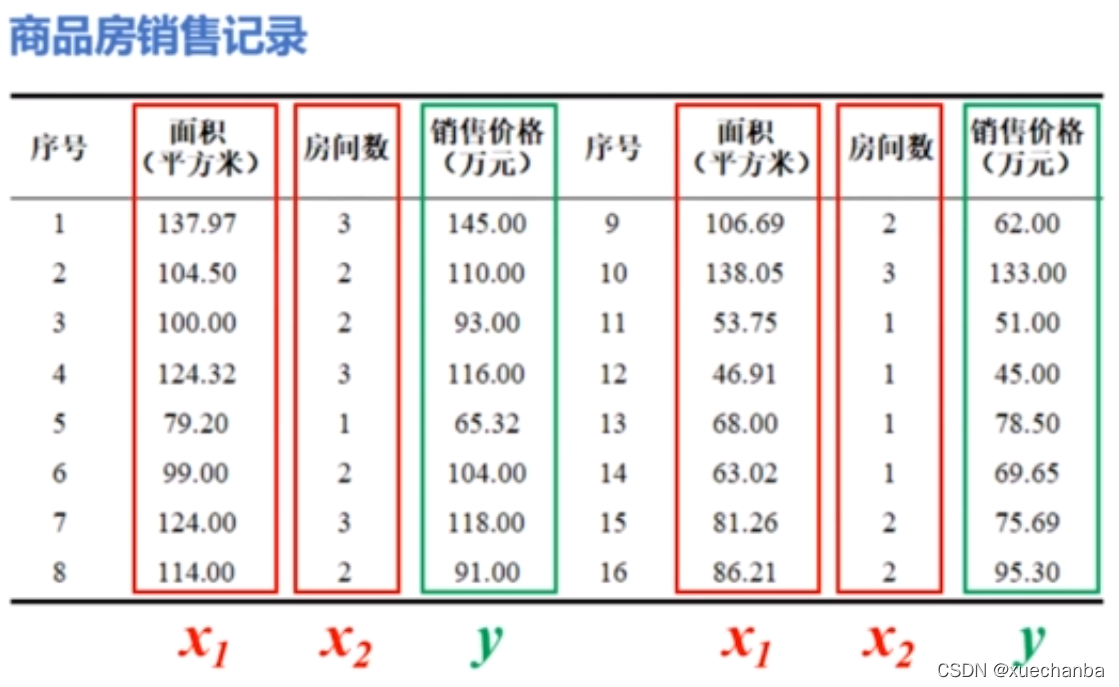
需要注意的是，如果直接使用上图中的数据 x1 和 x2 来训练模型，就会因为面积（x1）值远远大于房间（x2）值而造成在学习过程中占主导，甚至决定性的地位，这显然是不合理的。

那应该怎么解决呢？

这时候应该将各个属性值进行归一化。

归一化

归一化又被称为标准化，是将数据的值限制在一定的范围之内。

在机器学习中，对所有属性进行归一化处理就是让它们处于同一个范围、同一个数量级下。这样才能更加的具有合理性。

使用归一化处理后，不仅可以使得模型更快的收敛到最优解，还可以提高学习器的精度。

归一化可以分为线性归一化、线性归一化、非线性映射归一化。

1、线性归一化

线性归一化是对原始数据的线性变换，转换函数如下：

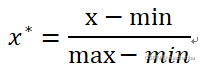
线性归一化实现对原始数据的 等比例缩放。
归一化之后，所有的数据都会被映射到 [0，1] 之间。

这种归一化方法适合于样本数据分布比较均匀，比较集中的情况，而如果最大值或最小值不稳定，或者和绝大多数数据差距比较大的情况，使用这种方法得到的结果也会不稳定，为了避免这种情况，在实际应用中，可以使用经验常量来代替最大值和最小值。

2、标准差归一化

将数据集归一化为均值为0，方差为1的标准正态分布，转换函数如下：

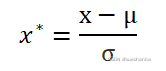
其中，μ是均值，σ是标准差。
标准差归一化适合于样本近似于正态分布或者最大值和最小值未知的情况，有时最大值和最小值处于孤立点的情况也适用。

3、非线性映射归一化

对原始数据的非线性变换。常用的映射方法有指数、对数和正切等。非线性映射归一化适合于数据分化比较大的情况，也就是有的数据特别大、有的比较小。通过这种非线性映射归一化后，可以使数据变的更加均匀或者有特点。

样本数据的归一化需要根据实际数据的分布情况和特点来决定采用哪种方法。

这里的数据归一化方式选择线性归一化，归一化结果如下：

import numpy as np
import matplotlib.pyplot as plt

# 第一步：加载数据
# area 是商品房面积
area = np.array([137.97, 104.50, 100.00, 124.32, 79.20, 99.00, 124.00, 114.00,
                 106.69, 138.05, 53.75, 46.91, 68.00, 63.02, 81.26, 86.21])  # (16, )

# room 是商品房房间数
room = np.array([3, 2, 2, 3, 1, 2, 3, 2,
                 2, 3, 1, 1, 1, 1, 2, 2])

# 第二步：样本数据归一化 —— 采用线性归一化
# x1 是商品房面积归一化后的结果
x1 = (area - area.min()) / (area