大模型必知基础知识：8、Transformer架构-如何理解学习率 Learning Rate

大模型必知基础知识：8、Transformer架构-如何理解学习率 Learning Rate

总目录

1. 大模型必知基础知识：1、Transformer架构-QKV自注意力机制
2. 大模型必知基础知识：2、Transformer架构-大模型是怎么学习到知识的?
3. 大模型必知基础知识：3、Transformer架构-词嵌入原理详解
4. 大模型必知基础知识：4、Transformer架构-多头注意力机制原理详解
5. 大模型必知基础知识：5、Transformer架构-前馈神经网络（FFN）原理详解
6. 大模型必知基础知识：6、Transformer架构-提示词工程调优
7. 大模型必知基础知识：7、Transformer架构-大模型微调作用和原理详解
8. 大模型必知基础知识：8、Transformer架构-如何理解学习率 Learning Rate
9. 大模型必知基础知识：9、MOE多专家大模型底层原理详解
10. 大模型必知基础知识：10、大语言模型与多模态融合架构原理详解
11. 大模型必知基础知识：11、大模型知识蒸馏原理和过程详解
12. 大模型必知基础知识：12、大语言模型能力评估体系
13. 大模型必知基础知识：13、大语言模型性能评估方法

目录

1. 学习率的基本概念
2. 用"下山"比喻理解学习率
   • 2.1 步子太大的情况
   • 2.2 步子太小的情况
   • 2.3 合适的步长
3. 学习率的工作原理
   • 3.1 机器学习的迭代过程
   • 3.2 梯度与方向
   • 3.3 数学公式解析
4. 学习率调整实例
5. 学习率的常见问题
   • 5.1 学习率过大导致的梯度消失
   • 5.2 学习率过小导致的收敛缓慢
6. 如何选择合适的学习率
   • 6.1 经验起步值
   • 6.2 动态调整策略
   • 6.3 可视化监控
7. 总结

---

1. 学习率的基本概念

在机器学习和深度学习中，学习率(Learning Rate)是一个听起来很高大上的术语，但其实它的概念非常贴近我们的日常生活。简单来说，学习率就是模型在学习过程中每次调整参数时"迈步子的大小"。

想象一下你在学习一项新技能，比如打篮球。如果你每次调整投篮姿势时改动太大，可能会越调越偏；如果每次只改动一点点，进步就会非常缓慢。学习率就是控制这个"改动幅度"的参数，它直接影响着模型训练的效率和最终效果。

在神经网络训练中，学习率是一个超参数，它决定了模型权重在每次迭代中更新的幅度。选择合适的学习率对于模型能否成功训练至关重要。

2. 用"下山"比喻理解学习率

为了更好地理解学习率的作用，我们可以用一个非常形象的比喻：假设你现在在一座山顶，想走到山脚下，但是你的眼睛被蒙住了（不考虑掉下悬崖安全情况），只能通过脚下的坡度来判断方向。每次你都要决定迈多大的步子往下走，这个"步子的大小"就相当于学习率。

在这个比喻中，山顶代表损失函数的高值区域，山脚则代表损失函数的最小值点，也就是我们希望模型达到的最优状态。下山的过程就是模型训练的过程，而每一步的大小就是学习率决定的。

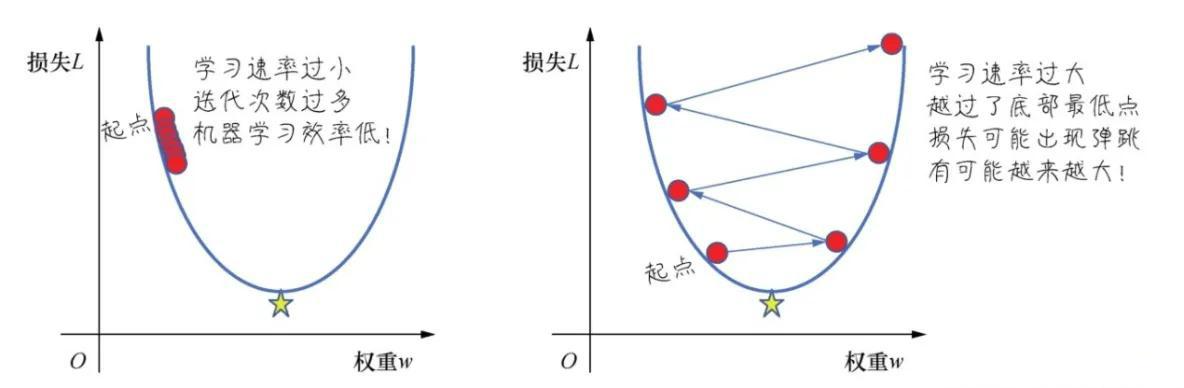
2.1 步子太大的情况

当学习率设置得过高时，就像你每次迈的步子太大。这样会带来几个问题：

首先，你可能会一步跨过山谷，直接踩到对面的山坡上。在模型训练中，这意味着参数更新幅度太大，可能会越过最优解，导致损失值不降反升。

其次，你可能会在山谷两侧来回跳跃，永远无法稳定地到达谷底。这种现象在训练中表现为损失函数剧烈震荡，模型无法收敛。更糟糕的情况是，模型的损失值可能会越来越大，完全偏离正确的方向，这就是所谓的训练失败或发散。

从数学角度来看，过大的学习率会导致权重更新过度，使得模型在参数空间中跳跃式移动，错过了最优解所在的区域。

2.2 步子太小的情况

相反，当学习率设置得过低时，就像你每次只挪动很小的一点点。虽然这样比较安全，不会走错方向，但会带来效率问题。

你可能需要走成千上万步才能到达山脚，这在模型训练中意味着需要非常多的迭代次数，训练时间会变得非常漫长。在实际应用中，这可能导致训练过程需要几天甚至几周才能完成，大大增加了计算成本。

更严重的问题是，你可能会被山路上的小坑困住。由于步子太小，你可能无法跨越这些小坑，最终停在一个局部最优解的位置，误以为已经到达了山脚，但实际上距离真正的最优解还很远。

在深度学习中，局部最优解是一个常见问题，过小的学习率会增加陷入局部最优的风险，导致模型性能无法达到理想状态。

2.3 合适的步长

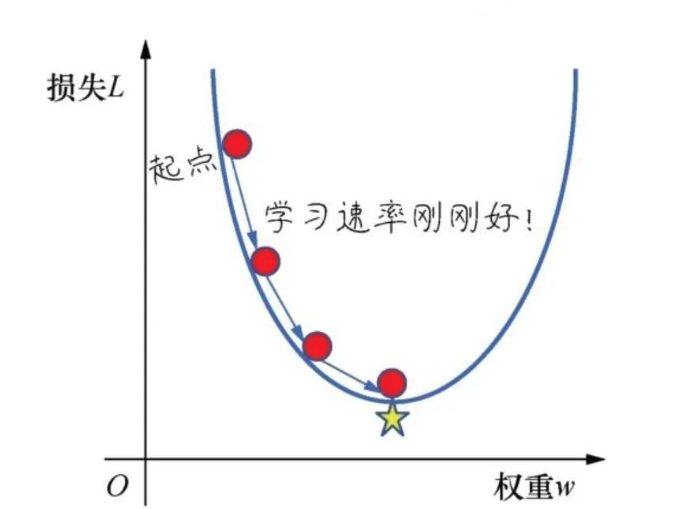
理想的学习率应该既能保证稳步下山，又能保持较高的效率。就像一个经验丰富的登山者，会根据地形的陡峭程度调整步伐大小，在平缓的地方可以快步走，在陡峭的地方则需要小心谨慎。

合适的学习率能够使模型快速收敛到最优解附近，同时在接近最优解时能够进行精细调整，最终稳定在一个很好的位置。这种平衡是模型训练成功的关键。

3. 学习率的工作原理

3.1 机器学习的迭代过程

机器学习和深度学习的本质是一个不断试错和改进的过程。具体来说，模型训练遵循以下步骤：

第一步，模型根据当前的参数对输入数据进行预测，得到一个输出结果。

第二步，将预测结果与真实的标签进行比较，计算出两者之间的差距，这个差距就是损失值(Loss)。

第三步，根据损失值计算梯度，确定应该向哪个方向调整参数才能减小损失。

第四步，使用学习率乘以梯度，得到参数的更新量，对模型参数进行调整。

第五步，使用更新后的参数重新进行预测，开始下一轮迭代。

这个过程会重复成千上万次，每次都让模型离最优解更近一步。学习率在第四步中起到了关键作用，它决定了每次参数更新的幅度。

3.2 梯度与方向

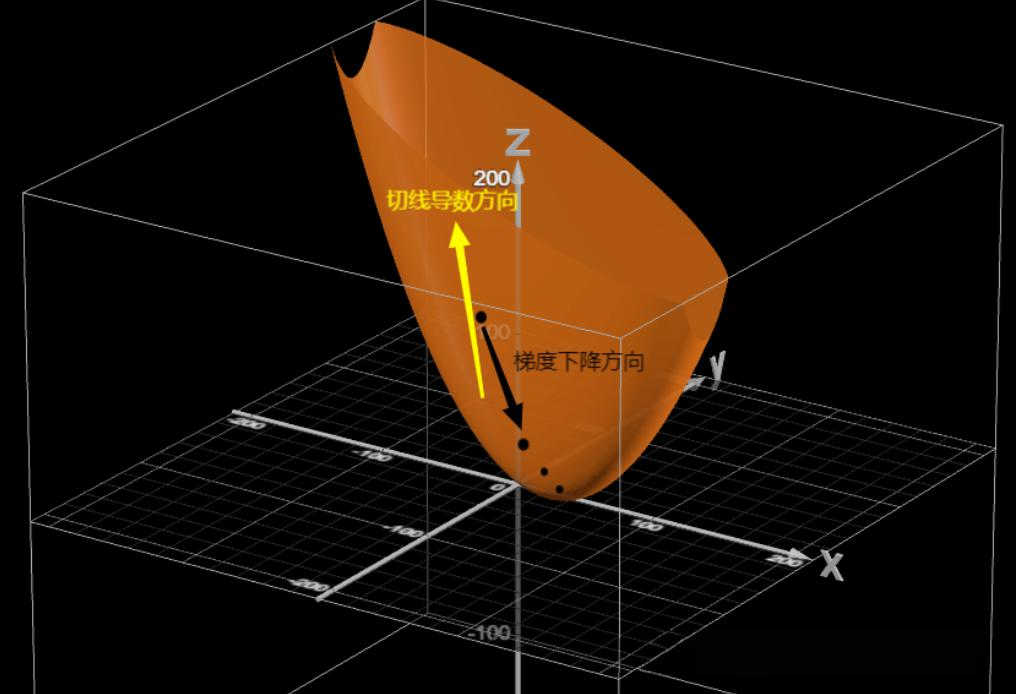
在理解学习率之前，我们需要先理解什么是梯度。梯度本质上是损失函数对模型权重参数的偏导数，它告诉我们两个重要信息：

首先是方向信息。梯度指向损失函数增长最快的方向，因此梯度的反方向就是损失下降最快的方向。我们需要沿着梯度的反方向更新参数，这样才能让损失值减小。

其次是幅度信息。梯度的大小反映了损失函数在当前位置的陡峭程度。梯度越大，说明坡度越陡，我们就越需要进行较大幅度的调整。

通过求偏导数，我们可以得到损失函数的切线方向。结合学习率这个参数，我们就同时拥有了方向和步长两个要素。在多维参数空间中，模型沿着梯度的反方向，以学习率决定的步长不断移动，逐步逼近真实值对应的参数配置。

经过多轮更新后，模型会找到最接近真实值的权重参数组合，这时我们就说模型学到了知识，掌握了数据中的规律。

3.3 数学公式解析

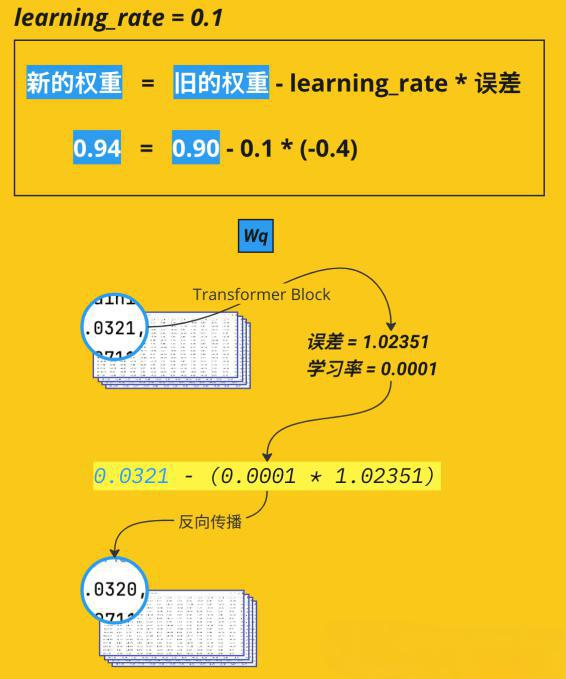
学习率的数学表达式非常简洁。参数更新的基本公式为：

新的权重 = 旧的权重 - 学习率 × 梯度

用数学符号表示就是：

$$w_{new}=w_{old}-\eta \times \nabla L(w)$$

其中，$w$ 表示模型的权重参数，$\eta$ (eta)表示学习率，$\nabla L(w)$ 表示损失函数对权重的梯度。

举个具体的例子，假设当前权重为0.90，梯度计算结果为-0.4，学习率设置为0.1，那么：

新权重 = 0.90 - 0.1 × (-0.4) = 0.90 + 0.04 = 0.94

可以看到，因为梯度是负数，实际上参数是在增加。这是因为负梯度方向意味着增加参数可以减小损失。

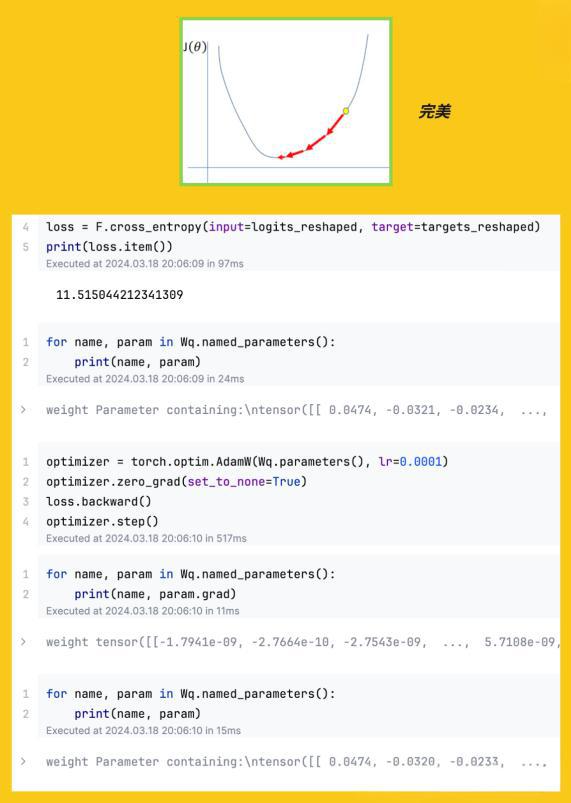
在实际的深度学习框架中，比如在Transformer的训练过程中，这个更新过程会在每个参数上同时进行。假设一个Transformer块中的某个权重参数Wq当前值为0.0321，经过前向传播和反向传播后，计算得到的损失为1.02351，对应的梯度为0.0001。使用学习率0.0001进行更新：

新权重 = 0.0321 - (0.0001 × 1.02351) = 0.0321 - 0.0001024 ≈ 0.0320

这个微小的调整会让模型的预测更加准确，经过数百万次这样的更新，模型就能学会复杂的模式。

4. 学习率调整实例

让我们通过一个日常生活中的例子来进一步理解学习率的作用。假设你在玩打地鼠游戏，地鼠的位置是目标，你的锤子每次打偏了，就要根据偏差调整下一次的落点位置。

在第一次尝试中，假设地鼠出现在正中间，而你的锤子落在了左边20厘米的位置。这个20厘米的偏差就相当于梯度，它告诉你需要向右调整。

如果你的学习率很高，比如说你决定每次调整30厘米，那么下一次你的锤子会落在右边10厘米的位置，又打偏了。然后你再调整30厘米回到左边，就这样来回摇摆，永远无法准确击中目标。这就是学习率过高导致的震荡问题。

如果你的学习率很低，比如每次只调整1厘米，那么从左边20厘米移动到正中间，你需要调整20次。虽然最终能够击中目标，但效率太低，游戏可能早就结束了。这就是学习率过低导致的收敛缓慢问题。

合理的做法是，一开始偏差较大时，可以用较大的步长快速接近目标，比如一次调整10厘米。随着越来越接近目标，逐渐减小调整幅度，在接近目标时改为每次调整2-3厘米，最后在目标附近时改为每次调整0.5厘米进行精细调整。这种动态调整学习率的策略就是我们下面要讨论的学习率衰减方法。

5. 学习率的常见问题

5.1 学习率过大导致的梯度消失

当学习率设置得过大时，会出现一种被称为"梯度消失"或者更准确地说是"训练不稳定"的现象。虽然术语叫"梯度消失"，但实际上问题并不是梯度变成了零，而是参数更新太剧烈导致的一系列问题。

具体表现为，模型的损失函数曲线会像过山车一样剧烈波动。你会看到损失值忽高忽低，有时甚至会突然飙升到一个很大的数值。这说明模型在参数空间中跳跃式移动，无法稳定下来。

更严重的情况是，模型可能会完全"飞出"正确的参数范围。比如某些权重值变成了无穷大或者NaN(非数字)，导致训练过程崩溃。在这种情况下，无论训练多少轮，模型都无法学到任何有用的知识。

在Transformer等大模型的训练中，这个问题尤其需要注意。因为这些模型的参数量巨大，计算图很深，如果学习率不合适，很容易出现数值不稳定的情况。

5.2 学习率过小导致的收敛缓慢

学习率过小带来的问题虽然不像过大那样会导致训练崩溃，但同样会严重影响训练效果。

最直接的问题是训练时间过长。如果学习率太小，模型参数每次更新的幅度很小，就需要非常多的训练迭代才能收敛。原本可能几个小时就能完成的训练，可能需要好几天甚至几周。这不仅浪费计算资源，也会大大延长模型开发的周期。

另一个更隐蔽的问题是容易陷入局部最优解。在复杂的损失函数曲面上，存在许多局部的低谷区域。如果学习率太小，模型的参数更新幅度不足以跨越这些小的障碍，就会被困在一个局部最优解中，误以为已经找到了最好的参数配置。

实际上，可能在不远处就有一个更好的全局最优解，但由于步长太小，模型永远无法到达那里。这会导致模型的最终性能明显低于预期，无法充分发挥模型架构的潜力。

在实践中，我们经常会遇到这样的情况：将学习率从0.0001提高到0.001后，模型的最终准确率从85%提升到了90%，这就是因为更大的学习率帮助模型跳出了局部最优解。

6. 如何选择合适的学习率

6.1 经验起步值

选择学习率并没有一个万能的公式，很大程度上依赖于经验和实验。不过，研究者们通过大量实践总结出了一些常用的起步值。

对于传统的优化器如SGD(随机梯度下降)，常见的起步学习率是0.1、0.01或0.001。通常建议从0.01开始尝试，这是一个相对中庸的选择。如果训练初期损失下降很慢，可以尝试提高到0.1；如果出现震荡或者损失不降反升，则需要降低到0.001甚至更小。

对于Adam等自适应优化器，推荐的默认学习率通常是0.001或0.0001。这些优化器会自动调整每个参数的学习率，因此相对来说对初始学习率不那么敏感。

对于大规模的Transformer模型训练，由于模型规模巨大，通常需要使用较小的学习率，比如0.0001到0.00001之间。同时，还需要配合学习率预热(Warmup)等技巧，这个我们在下一节会详细讨论。

值得注意的是，学习率的选择还与批次大小(Batch Size)有关。一般来说，批次越大，可以使用越大的学习率。有一个简单的经验法则：当批次大小翻倍时，学习率也可以翻倍。

6.2 动态调整策略

在实际训练中，我们很少从头到尾使用固定不变的学习率。相反，会采用各种动态调整策略，让学习率随着训练过程的推进而变化。

学习率衰减(Learning Rate Decay)

这是最常用的策略之一。基本思想是：训练初期可以用较大的学习率快速接近最优解，训练后期则需要用较小的学习率进行精细调整。

常见的衰减方式包括：

1. 阶梯衰减：每隔一定的训练轮次，将学习率减半或乘以0.1。比如每30个epoch将学习率乘以0.1。

2. 指数衰减：学习率按照指数函数平滑地递减。公式为：学习率 = 初始学习率 × 衰减率^(当前步数/衰减步数)

3. 余弦衰减：学习率按照余弦曲线的形式从初始值平滑地降低到接近零，这种方式在许多计算机视觉任务中表现很好。

学习率预热(Warmup)

在训练Transformer等大模型时，经常会使用预热策略。在训练的最开始几个epoch或几千步，让学习率从一个很小的值逐渐增加到目标值。

这样做的原因是，训练初期模型参数是随机初始化的，损失函数的梯度可能很不稳定。如果一开始就使用较大的学习率，可能会导致参数更新过大，使训练过程不稳定。通过预热让模型先用小学习率适应数据分布，然后再逐步提高学习率，可以显著提高训练的稳定性。

自适应优化器

像Adam、RMSProp、AdaGrad等优化器会自动为每个参数调整学习率。这些方法的核心思想是：对于更新频繁的参数使用较小的学习率，对于更新稀疏的参数使用较大的学习率。

Adam优化器结合了动量方法和自适应学习率，是目前最流行的优化器之一。使用Adam时，你只需要设置一个全局的学习率，优化器会自动处理每个参数的具体更新幅度。这大大简化了调参的工作，也是为什么Adam在深度学习社区如此受欢迎的原因。

6.3 可视化监控

在训练过程中，我们需要实时监控各种指标来判断学习率是否合适，并及时做出调整。

观察损失曲线

损失曲线是最直接的判断依据。一个健康的训练过程，损失曲线应该是平滑下降的。

如果损失曲线像过山车一样剧烈震荡，忽高忽低，这明确表示学习率过大。需要将学习率减小，通常减半或者降低一个数量级。

如果损失曲线几乎是一条平线，长时间没有明显下降，可能是学习率太小。可以尝试将学习率提高2-10倍。

如果损失先是快速下降，然后突然开始震荡或上升，可能是一开始学习率合适，但随着接近最优解，需要更小的学习率来进行精细调整。这时应该引入学习率衰减策略。

绘制学习率变化曲线

同时绘制学习率的变化曲线也很有帮助。可以清楚地看到学习率是如何随训练过程调整的，以及这种调整如何影响了损失的变化。

学习率范围测试(LR Range Test)

这是一种系统性寻找最佳学习率的方法。在正式训练前，用少量数据进行一次快速测试：从一个非常小的学习率开始，比如1e-8，在每个批次后逐渐增大学习率，一直到损失开始发散为止。记录整个过程中的损失变化，绘制出损失与学习率的关系图。

通常，你会看到一个先快速下降后上升的曲线。最佳学习率一般在损失下降最快的位置，或者是损失最低点对应学习率的1/3到1/10之间。

这种方法可以快速找到一个合理的学习率范围，避免了盲目尝试的低效率。

7. 总结

学习率是机器学习和深度学习中最重要的超参数之一，它本质上是平衡训练速度和模型精度的杠杆。通过对学习率的深入理解，我们可以得出以下几点启示：

第一，学习率不是一个万能值，没有一个适用于所有情况的完美学习率。它需要根据具体的模型架构、数据集特点、批次大小等因素来调整。

第二，欲速则不达，过大的学习率虽然可能让训练在初期进展很快，但往往会导致模型无法收敛，甚至训练崩溃。在设置学习率时，宁可保守一些，也不要过于激进。

第三，慢工出细活，但也不能过于保守。过小的学习率虽然安全，但会大大延长训练时间，增加计算成本。更重要的是，可能导致模型陷入局部最优，无法达到理想的性能。

第四，自我改革才能进步，在实际应用中，我们应该采用动态调整策略，让学习率随着训练过程而变化。训练初期可以用较大的学习率快速接近最优解，训练后期则需要用较小的学习率进行精细调整。

第五，借助工具和可视化，现代深度学习框架提供了丰富的工具来监控和调整学习率。要善于利用这些工具，通过可视化实时了解训练状态，及时发现问题并做出调整。

第六，经验和实验的重要性。虽然有很多经验法则和理论指导，但找到最适合特定任务的学习率，仍然需要大量的实验和调试。不要害怕尝试不同的值，通过系统的实验积累经验，逐步建立对学习率的感觉。

在Transformer等大模型的训练中，合理设置学习率特别关键。这些模型参数量巨大，训练成本很高，一个糟糕的学习率设置可能导致几天甚至几周的训练时间白白浪费。因此，在开始大规模训练之前，建议先在小规模数据上进行充分的学习率调试，找到一个合理的范围，然后再进行完整的训练。