医疗物联网多标准接收器设计

5 医疗物联网传感器网络的多标准接收器

5.1. 引言

IEEE 802.15.6标准[IEE 12a]专用于人体附近运行的无线通信，具有极低功耗和覆盖范围（3米），可提供可靠的医疗服务（如生命体征参数测量）以及实时娱乐等非医疗服务。

与802.15.6标准的超宽带模式不同，窄带模式[LEE 09]旨在成为医疗行业物联网（IoT）的参考标准[CHE 15]。正因为如此，且不同于LEE 09、CHO 10、MAT 15、MAT 14、LIA[的研究，本章专注于该模式。然而，IEEE 802.15.6标准的窄带模式必须在2.4 GHz ISM频段与诸如IEEE 802.11a/b/g/n（WiFi）[IEE 12b], IEEE 802.15.1（蓝牙）[IEE 05]以及IEEE 802.15.4（ZigBee）[IEE 15]等强大竞争者共存。

为了推动IEEE 802.15.6标准窄带模式的发展，我们提出了一种类似[MIC 01]（具有多个正交子载波）的正交频分复用接收机，该接收机可例如被用于传统的WiFi接收器，然后将其用作多标准接收器。

本章结构如下：在第5.2节中，我们将回顾一般背景，并描述WiFi标准802.11a/n/ac的特性。第5.3节将回顾WBAN标准信号的特定性。第5.4节详细说明为802.15.6标准在窄带模式下提出的物理层设计。第5.5节讨论仿真结果。最后，将给出各种结论。

5.2. 通用上下文

5.2.1. 正交频分复用

多载波技术是在1957[DOE 57]中发明的。其基本思想是将待传输信号的频谱划分为 个子信道，以简化均衡并利用频率分集。

考虑一个由 个符号 ૙、 ૚、⋯⋯、 ି૚组成的序列，其中是一 个实数或复数符号。调制原理是将每个符号在载波上传输。因此，调制信号可以表示为：

$$ ()= \sum \frac{2\pi}{T} e^{j2\pi f_k t} $$

遗憾的是，调制器/解调器的复杂度使得该方法难以应用。直到离散傅里叶变换[WEI71]被发现，处理电路才在20年后具备了实现正交多载波技术的能力。

如果频率之间的间隔为ࢤ= ૚ （其中为符号周期），则复用[5.1]是正交的。

因此，调制信号变为：

$$ ()= \frac{2\pi}{T_0} \sum_{k=0}^{N-1} e^{j2\pi (f_0 + k\Delta f)t} $$

其中 ૙是中心频率。

容易注意到，[5.2]的第二项是带限的，其最大频率为= ૛ 。因此，我们可以在=时刻对其采样。这些采样可以表示如下：

$$ ()=()= \sum_{k=0}^{N-1} e^{j2\pi (k/N)n} $$

[5.3]表明，待传输信号的采样仅是序列 ૙, ૚, … . ି૚的逆傅里叶变换。

因此，无噪声情况下接收信号的采样时刻= , =૙, …, −૚可表示为：

$$ ࢠ()=ࢠ()= \sum_{k=0}^{N-1} H_k e^{j2\pi (k/N)n} $$

其中 是第k个载波上信道的增益。

因此，我们只需对序列ࢠ૙, ࢠ૚, …, ࢠ ି૚进行傅里叶变换，并对其进行均衡，以得到序列 ૙, ૚, …, ି૚。

这种调制/解调技术在WiFi中被广泛使用。

5.2.2. IEEE 802.11a/b/g/n/ac 标准的特性

IEEE 802.11 标准最初定义了三种类型的跳频扩频、直接序列扩频和红外物理层。该标准并非一成不变。事实上，多年来， 802.11a/b/g/n/ac 标准对其进行了多次修订。表5.1 按时间顺序总结了最早出现的这些标准的特性。

标准	传输	频率 band	最大 吞吐量	调制
802.11a	OFDM	5 GHz	54兆比特每 秒	差分二进制相移键控, 差分正交相移键控, 16进制正交幅度调制，64进制正交 幅度调制
802.11b	DSSS	2.4吉赫兹	11兆比特每 秒	差分二进制相移键控， 差分正交相 移键控
802.11g	OFDM	2.4吉赫兹	54兆比特每 秒	差分二进制相移键控，差分正交相移键控，16进制正交幅度调制, 64进制正交 幅度调制

表5.1 802.11a/b/g 标准的特性

正交频分复用波形基于长度为64的IFFT。为了减小邻道泄漏的影响，仅使用64个载波中的52个。表5.2规定了IEEE 802.11a/g标准的正交频分复用参数。

参数	值
ܰௌ஽：数据子载波数量	48
ܰௌ௉：导频子载波数量	4
ܰௌ்：总子载波数量	52
∆ி：子载波频率间隔	0.3125 MHz
ܶிி்：FFT/IFFT周期	3.2 μs
ܶௌூீே஺௅：OFDM符号持续时间	4 μs
ܶீூ：保护间隔持续时间	0.8 μ秒
占用带宽	16.6 兆赫
总带宽	20 MHz

表5.2. IEEE 802.11a/g的正交频分复用参数

IEEE 802.11n 标准通过使用 MIMO（多输入多输出）系统改进了 802.11a/g 标准，可提供理论上高达 540 Mbps 的吞吐量。IEEE 802.11ac 标准进一步提升了吞吐量，并支持多用户传输。该标准支持两个不同的频段，即 2.4吉赫兹 和 5 GHz。

所有基于OFDM的802.11a/g/n/ac标准帧均由以下字段组成：

图5.1。 802.11a/n/ac帧的结构。有关该图的彩色版本，请参见 www.iste.co.uk/saleh/challenges.zip

802.11a 标准中的前导码部分包括 L‐STF（传统短训练字段）和 L‐LTF（传统长训练字段）。对于更先进的标准，如使用 MIMO 技术的 802.11n/ac，前导码还包括第二部分，包含 X‐STF 和 X‐LTF，其中字母 X 表示 802.11n 的 HT（高吞吐量）或 802.11ac 的 VHT（非常高吞吐量）。传统前导码的第一部分用于区分同一频段内的不同 802.11 标准，并标记所有 802.11a/n/ac 代际的帧起始位置。L‐STF 包含一个短序列的 10 次重复，持续时间为 0.8 μs，供接收机用于检测帧头、控制增益（ AGC—自动增益控制）以及估计频率偏移（CFO—载波频率偏移）。随后的 L‐LTF 字段包含一个长度为 3.2 μs 的序列的 2.5 次重复，可用于精细帧同步和信道估计等功能。L‐GIS（传统信令）字段包含有关 802.11a 数据调制和编码参数的信息。对于 802.11n/ac，X‐SIG 字段则包含特定的数据调制和编码信息。

5.3. IEEE 802.15.6标准

医疗网络满足非常特定的需求。在底层，支持传感器的节点通常是一次性的，因此通信的低复杂度和低功耗至关重要。此外对象可以与人体进行交互，例如胰岛素泵的情况。因此，通信的可靠性是一个首要需求，有时甚至是至关重要的，因为这些传感器在紧急情况下可能会传输关键信息。最后，个人医疗数据必须严格保密，这就带来了严格的安全约束；特别是无线网关与互联网的接口。

传统的个人区域网络（PAN）、WiFi和蓝牙并非为满足所有这些需求而开发，也无法原生支持这些要求。因此，IEEE 802.15工作组专门成立了一个工作组，以标准化OSI模型的两个底层（物理层和数据链路层）。这项研究最终形成了IEEE 802.15.6标准。此外，还针对接近医疗需求的用户案例（如体育活动、体育和游戏）开发了其他相关规范。

WBAN标准提供了广泛的吞吐量，因此可支持多种应用。该标准在多个频段上运行，如图5.2所示。它在全球范围内的ISM频段（工业、科学和医疗）上运行，因此与包括WiFi在内的多个标准共存。

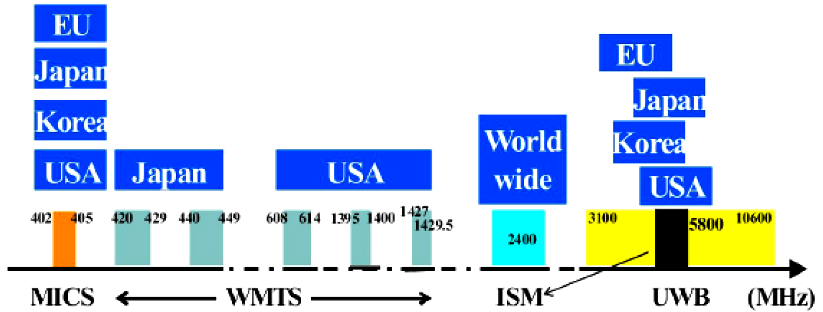
图5.2 WBAN频段。有关该图的彩色版本，请参见 www.iste.co.uk/saleh/challenges.zip

5.3.1. WBAN帧

图5.3 展示了IEEE 802.15.6标准的帧结构。它由三个字段组成，即物理层汇聚协议（PLCP）前导码、PLCP头部和物理层服务数据单元（PSDU）。后两个部分称为物理层协议数据单元（PPDU）。

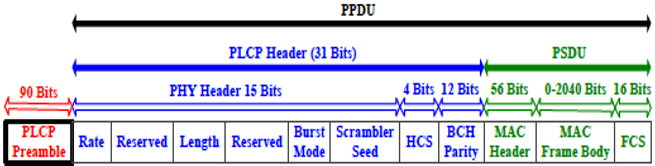
图5.3 WBAN帧的结构。有关该图的彩色版本，请参见 www.iste.co.uk/saleh/challenges.zip

第一个PLCP前导码字段是一个接收机已知的训练序列，用于帧同步、时间同步和频率同步等多种基带处理。对于窄带模式，定义了两个前导码，以减少因网络使用相邻信道而引起的误报。每个序列通过将 63位与以下27位010101010101101101101101101连接而成。该字段采用ߨ/2‐差分二进制相移键控作为调制方式，包含恰好90个复数符号。PLCP头部帧的第二个字段由31位组成，包含有关传输的信息，如调制和编码参数。由于该字段也采用ߨ/2‐差分二进制相移键控作为调制方式，因此包含31个复数符号。最后一个帧字段称为PSDU，包含有用信息。

5.3.2. WBAN物理层的特性

PLCP头部字段和PSDU分别采用BCH (31,19)和BCH (63,51)代数码进行编码。实际上，BCH (31,19)码是通过在待编码字中添加32个零而得到的BCH (63,51)码的缩短形式，如图5.4所示。

图5.4. BCH(31,19)

19 个信息位	32 零位	12个校验位

编码后，这些字段按顺序交织，以增加多样性 [SZC 15], ，然后使用生成器 ݃(ݔ) =1+ݔ²+ݔ¹²+ݔ¹³+ݔ¹⁴ 进行扰乱。

图5.5. WBN扰码器

图5.6. WBAN通信系统。有关此图的彩色版本，请参见 www.iste.co.uk/saleh/challenges.zip

对于窄带模式，该字段的二进制序列通过以下三种差分调制之一进行调制：ߨ/2‐差分二进制相移键控、ߨ/4‐差分正交相移键控或ߨ/8‐D8PSK。

对于每种调制方式，比特流被转换为符号序列 ݏ(݇)，݇= 0，1，⋯，(ܰ/݈݋݃₂(ܯ)) −1 ，如下所示：

$$ ݏ(݇)=ݏ(݇ −1)\exp(j߮_k), $$

其中，M 为调制阶数，且以 ݏ(−1) = \exp (jߨ/2) 作为第一个前导码符号的参考。符号 ߮_k 之间的过渡值分别在表5.3、5.4和5.5中给出，对应于 ߨ/2‐差分二进制相移键控、ߨ/4‐差分正交相移键控和 ߨ/8‐D8PSK。

ܾ(݇)	߮_k
0	ߨ/2
1	‐ߨ/2

表5.3. ߨ/2-差分二进制相移键控

ܾ(2݇),ܾ(2݇+1)	߮_k
0,0	ߨ/4
0,1	3ߨ/4
1,0	7ߨ/4
1,1	5ߨ/4

表 5.4. ߨ/4-差分正交相移键控

ܾ(2݇)，ܾ(2݇+1)，ܾ(2݇+3)	߮_k
0, 0, 0	ߨ/8
0, 0, 1	3ߨ/8
0, 1, 0	7ߨ/8
0, 1, 1	5ߨ/8
1, 0, 0	15ߨ/8
1, 0, 1	13ߨ/8
1, 1, 0	9ߨ/8
1, 1, 1	11ߨ/8

表 5.5。 ߨ/8-D8PSK

由于覆盖范围小且传输速率低，该信道可被视为非选择性慢衰落信道。因此，接收信号可建模为：

$$ ݎ(ݐ)=ℎ \sum s_n u(t -nT_{sym})+w(t), $$

其中u(t)是升余弦根滤波器，h是信道衰减。在数据包传输期间可视为恒定。

接收端基带信号处理需要在进行符号检测之前完成帧同步、频率同步和时间同步。在物联网环境中，由于简单性和节能是重要因素，因此存在用于窄带同步的传统算法[NAS 16，GEL 16]。然而需要注意的是，由于采用符号的差分检测方式，这些调制方式无需进行相位同步。

5.4. 物理层设计

本节详细介绍了在多标准接收器正交频分复用上下文中用于帧同步、频率同步和时间同步的算法。

5.4.1. 帧同步

由于IEEE 802.15.6系统是一种数据包传输系统，在进行任何其他基带处理之前，首先需要完成的任务是定位数据包起始位置（SOF）。因此，该任务应能容忍多种不完美因素，如采样不良、频率偏移和加性噪声。

为了利用频率为݂௦௔௠௣= 2݂௦௬௠௕的采样后的接收信号实现鲁棒帧同步，提出以下算法：

$$ \hat{n} {SOF} = \arg\left{\max_n\left{\sum {l=1}^L \left|\sum_{p=-9}^{8} r\left(n+p+\frac{lT_{sym}}{T_{samp}}\right) r^*(n+p) \prod_{q=0}^{l} \exp(-j\tilde{\varphi}_{p+q}) \right|\right}\right}, \tag{5.7} $$

其中$\hat{n} {SOF}$是帧的估计起始位置，$r(n)$是接收信号的第$n$个观测值， $T {sym}= 1/f_{sym}$是符号周期，$\tilde{\varphi}_n$是符号$s(n -1)$和$s(n)$之间的相位转换。

需要注意两点：首先，相关项$r\left(n+\frac{lT_{sym}}{T_{samp}}\right)r^*(n)$减小了频率偏移的影响；其次，索引$l$表示相关性不仅在连续的符号之间进行评估，还在时间上相隔的符号之间进行评估，从而提高了算法的鲁棒性。

我们建议采用$L= 2$；这足以在存在频率偏移（CFO）$f_{CFO}= 0$、 $1f_{sym}$和信噪比（SNR）$SNR= -1 \text{dB}$的情况下定位帧的起始位置。

5.4.2. 频率同步

频率同步是需要执行的第二项任务，它对时间同步和最终的符号检测具有重要影响。我们开发的用于补偿发射机与接收机之间频率偏移的同步算法分为两个阶段：第一阶段进行粗频率同步，第二阶段进行细频率同步。

粗频率同步按如下方式进行：
1) 通过快速傅里叶变换将每个频域中的接收信号观测进行变换。这些频域中的观测表示为$\tilde{R}(k)$，$k = 0, 1, …, N_{IFFT}-1$。
2) 通过快速傅里叶变换将频域中的$N_{IFFT}/2$个前导符号进行变换。这些在频域中的观测值表示为$\tilde{P}(k)$，$k = 0, 1, …, N_{IFFT}/2-1$。
3) 在频域中定位两个序列之间的最大相关性，方法如下：

$$ \hat{n}_{coarse CFO} = \arg\left{\max_n\left{|A_n + B_n|\right}\right}, \tag{5.8} $$

其中

$$ A_n = \sum_{p=0}^{N_{IFFT}/2-1} \tilde{R}\big((p+n)\mod N_{IFFT}\big)\tilde{P}^*(p), \tag{5.9} $$

and
$$ B_n = \sum_{p=N_{IFFT}/4}^{N_{IFFT}/2-1} \tilde{R}\left(\left(p+ \frac{N_{IFFT}}{2}+n\right)\mod N_{IFFT}\right)\tilde{P}^*(p). \tag{5.10} $$

4) 补偿频率偏移 $\hat{f}_{coarse CFO}$。

需要注意的是，粗同步估计的值的精度在$f_{samp}/N_{IFFT}$范围内。因此，快速傅里叶变换的大小决定了算法的效率：快速傅里叶变换的尺寸越大，算法的精确度越高。

我们建议采用$N_{IFFT}= 128$。因此，对于每个包含90个前导符号的数据包，都有两个部分相关的估计值。

在完成粗频偏同步算法估计值的补偿后，进行细频率同步，步骤如下：

$$ \hat{f} {fine CFO} = \frac{1}{2\pi L T {sym}} \tan^{-1}\left(\sum_{l=1}^L \frac{1}{(90-l)} \sum_{p=0}^{8} \tilde{r}(n+l)\tilde{r}^*(p) \prod_{q=0}^{l} \exp(-j\tilde{\varphi}_{p+q}) \right). \tag{5.11} $$

为了降低系统的复杂度，频率偏移的精细估计按如下方式进行：

$$ \hat{f} {fine CFO} = \frac{1}{\pi T {sym}}\tan^{-1}\left(\hat{V}_{fine CFO}\right), \tag{5.12} $$

其中$\hat{V}_{fine CFO}$是通过一阶简单无限冲激响应（IIR）滤波器获得的：

$$ \hat{V} {fine CFO} = (1 -\alpha)\hat{V} {fine CFO} + \frac{\alpha}{l} \tilde{r}(p+l)^ \tilde{r}^ (p)\prod_{q=0}^{l} \exp(-j\tilde{\varphi}_{p+q}). \tag{5.13} $$

在第5.5节的仿真中，我们建议采用$L=2$和$\alpha= 0.01$。

5.4.3. 时间同步

该任务的目标是估计接收信号的时间间隔$\tau$，其中：

$$ r(t -\tau)=h \sum s_n u(t -nT_{sym} -\tau )+w(t -\tau). \tag{5.14} $$

与传统的由符号插值器和定时误差检测器（TED）两个模块组成的时间同步不同，所提出的算法倾向于估计信道的全局冲激响应$h u\big(t -nT_{sym} -\tau\big)$。因此，时间同步包含两个模块：信道估计和信道均衡。

信道估计器的目的是估计信道的频率传递函数，如下所示：
1) 对每个$N_{FFT}$接收信号观测在频域内进行快速傅里叶变换。这些频域中的观测表示为$\tilde{R}(k)$， $k= 0, 1, …, N_{FFT}-1$。
2) 在前导码的每对符号之间插入1个零。然后通过快速傅里叶变换（FFT）将所得序列在频域中每$N_{FFT}$点进行变换；频域中的观测值表示为$\tilde{P}(k)$， $k= 0, 1, …, N_{FFT}-1$。
3) 与OFDM系统的传统信道估计器一样，可以通过以下方式估计信道的频率响应：$\hat{H}(k)=\tilde{R}(k)/\tilde{P}(k)$。
4) 在 $\hat{H}(k)$ 的每对连续值之间对信道的频率响应进行线性插值。结果，我们得到一个新的信道传递函数 $\hat{H} I(k)$，其具有 $2N {FFT}$ 个点。

然后，信道均衡器触发重叠保留（OLS）方法 [PRO 07] ，以对频率补偿后的过采样接收信号观测进行频率均衡。它必须：
1) 采用上一个普通最小二乘法模块的$N_{FFT}$观测值；
2) 采用$N_{FFT}$新观测值进行均衡；
3) 将 $2N_{FFT}$观测值转换到频域——对应的点表示为 $R(k)$；
4) 执行均衡：$\hat{D}(k) =R(k)/\hat{H} I(k)$；
5) 将$\hat{D}(k)$的时域采样进行变换；
6) 提取最后的$N {FFT}$个采样点。每对采样点中的第一个提供 DMPSK符号。这使得可以在第5.5节中测量误码率（BER）。

我们建议采用$N_{FFT}= 64$。

5.5. 仿真结果

在本节中，针对以下两种场景，评估所提出的系统在 $\pi/2$‐DBPSK （图5.7）、 $\pi/4$‐DQPSK（图5.8）和 $\pi/8$ ‐D8PSK（图5.9）调制方式下的比特误码率（BER）性能：第一种场景是存在随机时间偏移 $\tau \in[-T_{sym}/2,T_{sym}/2]$的仿真（见标注为RTO sim的曲线）；另一种场景不仅包含随机时间偏移，还包含显著的频率偏移 $f_{CFO}= 0.1f_{sym}$（见标注为RTO + 10% CFO sim的曲线）。在这些仿真中，所有前述的基带处理模块均被启用（包括帧同步、频率同步和时间同步）。在加性白高斯噪声信道上可获得的最佳性能为理论性能（见标注为“theory”的曲线）[XIO 06, PRO 08], ，该性能是在假设发射机与接收机之间实现完美同步的条件下得出的。这些理论曲线为我们评估所提出系统的性能提供了绝对参考基准。

图5.7。所提出的系统在$\pi/2$‐差分二进制相移键控下的性能。有关该图的彩色版本，请访问www.iste.co.uk/saleh/challenges.zip

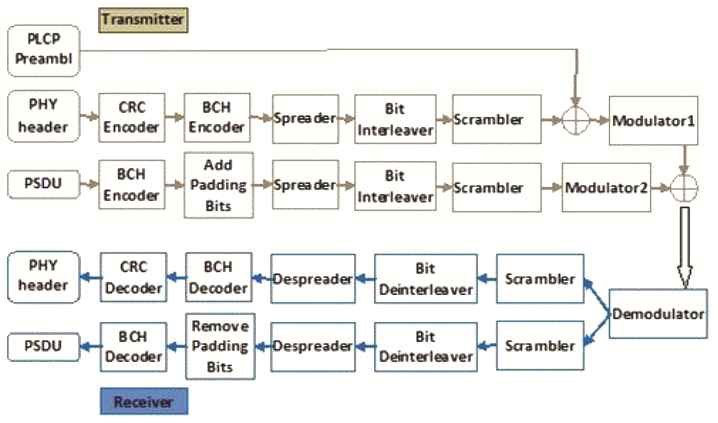
图5.8。所提出的系统在$\pi/4$‐差分正交相移键控下的性能。有关该图的彩色版本，请参见www.iste.co.uk/saleh/challenges.zip

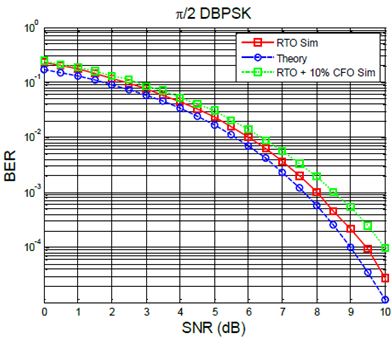
图5.9所提出的系统在$\pi/8$‐D8PSK下的性能。有关该图的彩色版本，请参见 www.iste.co.uk/saleh/challenges.zip

图5.7、5.8和5.9显示，所提出的系统在仅有随机时间偏移（RTO）的情况下，其误码率（BER）曲线仍非常接近最优理论性能。此外值得注意的是，在同步条件极为困难的情况下，并且考虑存在显著频率偏移带来的额外性能下降时，所提出的算法对于$\pi/2$‐差分二进制相移键控和$\pi/4$‐差分正交相移键控调制方式仍然保持鲁棒性。

5.6. 结论

本章提出了一种针对IEEE 802.15.6标准窄带模式的物理层算法设计。与单载波接收机物理层的传统设计不同，所提出的处理算法可直接应用于OFDM系统，例如WiFi。仿真结果表明，在具有随机时间偏移的高斯信道上，所研究算法的性能非常接近完美同步下的理论性能。这使得该设计在多标准多通道接收机的设计中具有吸引力，包括医疗物联网的应用。在后续研究中，我们希望在多标准接收器[VAN08]中引入软解码器，并采用可用于定位的跨层设计。