Algorithm-归并排序、快速排序

归并

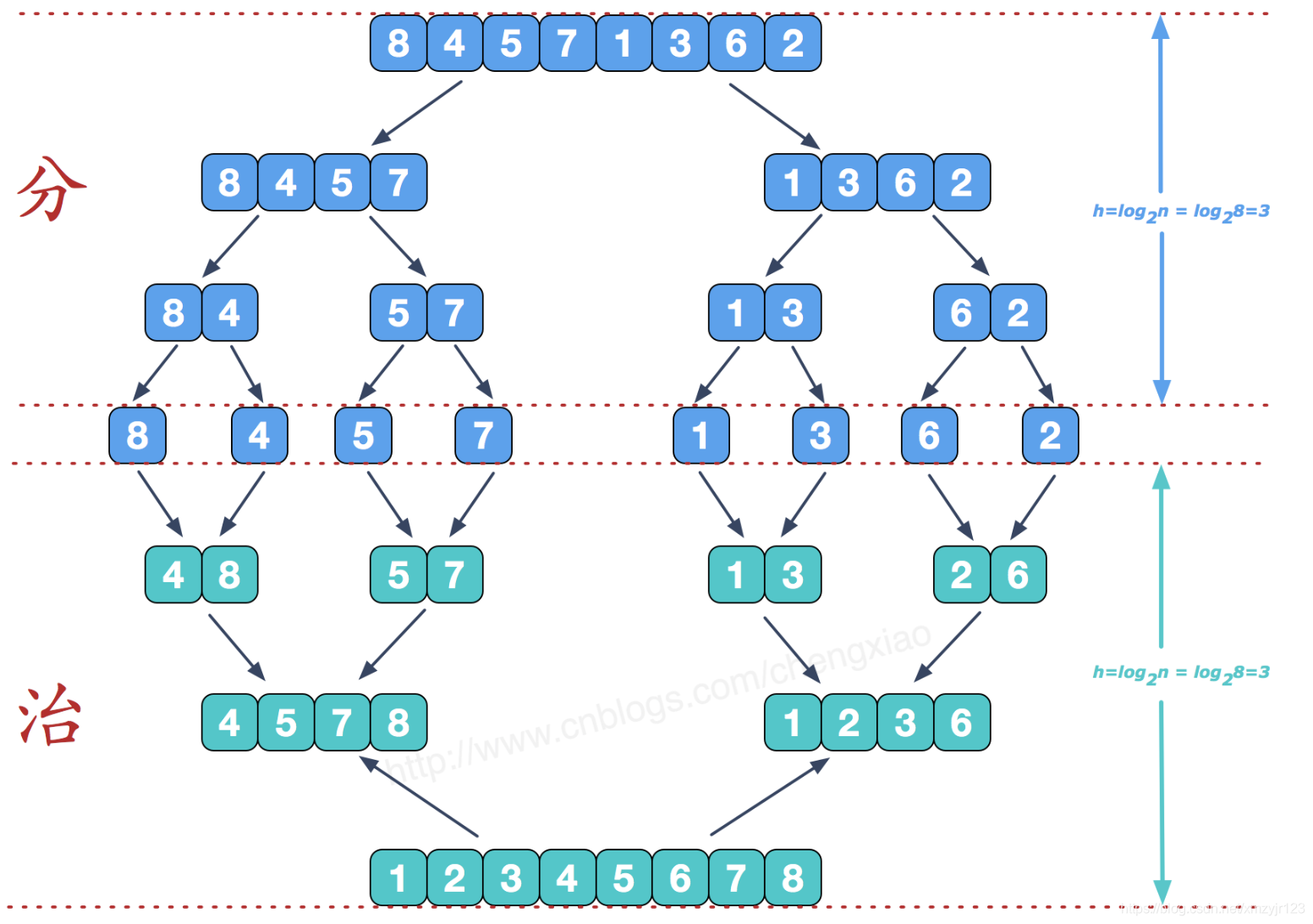
注：图是别人的.
由图可以看出来，归并就是：

1. 先将数组对半分，1分为2，2再对半分，一直分到只有单个的时候。
2. 对只能分到单个对时候停止分割，对两个进行比较排序，
3. 第一次排序好后，至少2个数是顺序的，之后是递归的过程，同理归并别的分组。

下面代码分析下：

	// a为需要排序的数组，low是低位，high是高位
    static void sort(int[] a, int low, int high) {
    	// 如果低位比高位低的话，就是还可以别分割，知道 low==high
    	// 例如：上图的 4 8，low=0，high=1
    	// 继续分割则是 4:low=0，high=0， 8:low=1，high=1
        if (low < high) {
        	// low=0，high=1 ，mid = 0
            int mid = (low + high) / 2;
            // 从这里可以体现 4:low=0，high=0
            // 不能再分割后就返回了
            sort(a, low, mid);
            // 8:low=1，high=1
            sort(a, mid + 1, high);
            // 所以第一次meger是这里，low=0，mid=0，high=1
            merge(a, low, mid, high);
        }
    }
    static void merge(int[] a, int low, int mid, int high) {
    	// 分配额外的数组，low 到 high需要的空间大小
        int[] temp = new int[high - low + 1];
        // 左边从low开始指的指针，会一直到mid
        int i = low;
        // 右边从mid+1开始，一直到high，因为我们需要对两个分组进行比较，排序
        int j = mid + 1;
        // 额外分组的指针
        int k = 0;
        // 2个分组都没到头就说明还是可以继续比较
        while (i <= mid && j <= high) {
        	// 比较，小的在temp的前面
            if (a[i] < a[j]) {
                temp[k++] = a[i++];
            } else {
                temp[k++] = a[j++];
            }
        }
        // 如果左边还没有结束，则继续进行分配
        while (i <= mid) {
            temp[k++] = a[i++];
        }
        // 右边也是这样
        while (j <= high) {
            temp[k++] = a[j++];
        }
        // 将重新排序好的temp 覆盖到a数组上面去
        for (int x = 0; x < temp.length; x++) {
            a[low + x] = temp[x];
        }
    }

快排

注：图片出处

// 递归实现
static void quickSort(int[] a, int low, int high) {
	// 左边不能大于右边，递归结束的地方
    if (low > high) return;
    // 我们从第一个开始取
    int temp = a[low];
    // 左边的第一个需要判断的下标
    int i = low + 1;
    // 最右边的下标
    int j = high;
    // 因为最终2个下标会重合，所以以i！=j为结束的标志
    while (i != j) {
    	// 从右边开始判断，如果大于就向左边移动，直到小于第一个取出来的数
        while (a[j] >= temp && i < j) {
            j--;
        }
        // 如果小于就向右移动，直到大于temp的数
        while (a[i] <= temp && i < j) {
            i++;
        }
        // 这里有个i<j的判断条件，因为有可能直接i等于j，那就是重合的部分和刚开始temp的位置交换
        if (i < j) {
            int temp1 = a[i];
            a[i] = a[j];
            a[j] = temp;
        }
    }
    // 和temp交换
    a[low] = a[i];
    a[i] = temp;
    // 递归排序左边
    quickSort(a, low, i - 1);
    // 递归排序右边
    quickSort(a, i + 1, high);
}