机器学习系列-KNN

简单概述：k-近邻算法采用测量不同特征值之间的距离方法进行分类。

k-近邻算法的一般流程

对未知类别属性的数据集中的每个点依次执行以下操作：

(1)计算已知类别数据集中的点与当前点之间的距离；

(2)按照距离递增次序排序；

(3)选取与当前点距离最小的几个点；

(4)确定前k个点所在类别的出现频率；

(5)返回前k个点出现频率最高的类别作为当前点的预测分类。

 

如下图所示，有两类不同的训练样本数据，分别用蓝色的小正方形和红色的小三角形表示，而图正中间的那个绿色的圆所标示的数据则是待分类的数据。

衡量待分类样本的周围的k个邻居的类别，k个邻居中哪个类别较多，就把该类别判给待分类样本。（K近邻思想）

【注意】：当然K不同，待分类样本被判别的类别也可能不同。

优缺点

优点：精度高，对异常值不敏感，无数据输入假定（没有初始值）

缺点：计算复杂度高、空间复杂度高

适用数据范围：数值型和标称型（离散型数据，变量的结果只在有限目标集中取值）

工作原理是

存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据与所属分类的对应关系。输人没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签。一般来说，我们只选择样本数据集中前k个最相似的数据，这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后，选择k个最相似数据中出现次数最多的分类，作为新数据的分类。

距离计算方法

K-近邻算法的核心在于找到实例点的邻居。要找邻居就要度量相似性。估量不同样本之间的相似性，通常采用的方法就是计算样本间的“距离”，相似性度量方法有：欧式距离、余弦夹角、曼哈顿距离、切比雪夫距离等。

 

1.欧式距离：欧式距离来源于欧式空间中的两点之间的距离公式。

二维平面上的两点：

2.曼哈顿距离

 

3.切比雪夫距离

 

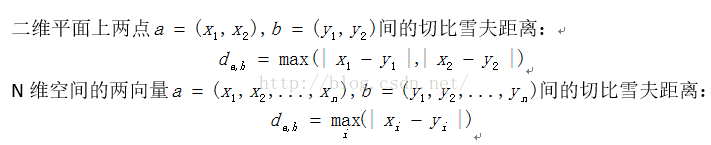
4.余弦距离

 K值选择

若k值较小，只有与输入实例较近（相似）的训练实例才会对预测结果起作用，预测结果会对近邻实例点非常敏感。如果近邻实例点恰巧是噪声，预测就会出错。容易发生过拟合。

若k较大，与输入实例较远的（不相似的）训练实例也会对预测起作用，容易使预测出错。k值的增大就意味着整体的模型变简单。

在应用中，k值一般取较小值。通常通过经验或交叉验证法来选取最优的k值。

分类决策规则

投票表决

少数服从多数，输入实例的k个近邻中哪个类的实例点最多，就分为该类。

加权投票法

根据距离的远近，对K个近邻的投票进行加权，距离越近则权重越大（比如权重为距离的倒数）。

归一化特征值

某一列的特征数值远远大于其他特征，这样在求距离的公式中就会占很大的比重，致使两点的距离很大程度上取决于这个特征，这当然是不公平的，我们需要所有特征都平均地决定距离，所以我们要对数据进行处理，使得每一列的取值范围都控制在0~1之间。

 

公式：newValue = (oldValue - min)/(max - min)

应用场景

分类，预测，等，可以参照大神的总结

详细介绍：https://coolshell.cn/articles/8052.html