Bloom Filter

最新推荐文章于 2025-01-16 08:28:33 发布

xlnjulp

最新推荐文章于 2025-01-16 08:28:33 发布

阅读量967

点赞数

分类专栏：数据结构

本文链接：https://blog.youkuaiyun.com/xlnjulp/article/details/26679683

版权

数据结构专栏收录该内容

6 篇文章

订阅专栏

本文深入探讨了Bloom过滤器的工作原理，包括其数据结构、插入查询操作、错误率计算及优化方法，并提供了具体实现案例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Bloom filter是一个高效的随机数据结构。Bloom filter定义一个大小为m的bit数组，定义k个hash函数。当插入一个新的元素e的时候，使用k个hash函数分别得到k个值hash1(e)，hash2(e)，……，hashk(e)，然后设置m[hash1(e)]，m[hash2(e)]，……，m[hashk[e]]为1。

如下图所示，m = 18，k = 3，插入的四个元素为x，y，z，w。拿x作为例子，hash1(x) = 1，hash2(x) = 5，hash3(x) = 13，所以m[1] = 1，m[5] = 1，m[13] = 1。

那么查询的时候是什么样子呢？比如查询x是否在Bloom filter中。跟插入的时候相类似，还是根据k个哈希函数，生成k个key，然后查询这些key在数组m中对应的bit位是否为1，如果都是1则表示在里面。那么可能会出现的问题就是有些数据不在Bloom filter中，但是根据上面的规则查询到的结果却是其在Bloom filter中，这就是falsepositive。

比如查询的数据是z，经过三个hash函数得到的三个key分别是，1，3，4。不巧的是，这三个位置的bit都已经被置为了1，虽然z没有插入过，但是得到的结果却是其也在bloom filter中。

通过上面的描述，可以看到Bloom filter相当于一个压缩算法，一个数据映射到bit数组后，仅仅只需要k个bit，就可以表示。比如一个int数据，如果采用正常存储的话，需要32个bit（在32位机器）。虽然会有需要一定的容错性，但是其空间利用优势还是很明显的。

A Bloom filter with 1% error and an optimalvalue of k, in contrast,requires only about 9.6 bits per element — regardless of the size of theelements. This advantage comes partly from its compactness, inherited fromarrays, and partly from its probabilistic nature. The 1% false-positive ratecan be reduced by a factor of ten by adding only about 4.8 bits per element.

出现错误的可能性

在这里我们假设k个hash函数设计的足够好，也就是说hash函数将某个元素映射到大小为数组中的任意位置的概率都是相同的，这个概率是1/m。

那么插入一个元素的时候，经过一个hash函数，数组中特定位不被设置为1的概率就是，

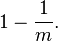
那么经过k个hash函数，特定位不被设置为1的概率是，

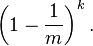
那么插入n个元素后，特定位仍然不被设置为1的概率是，

，也就是上面的概率的n倍。

相反的，特定位为1的概率就是，

那么对于一个新的元素，其对应的k个比特都是1的概率就是，

那么上面的结果是如何得出来的呢？根据，

所以，

最优的哈希函数个数

根据上面的公式，假设n，m都是常量，也就是需要推导公式与变量k之间的关系。

下面是具体的推导过程，

当k=(m/n) * ln2的时候，可以得到最小值p。那么当k=(m/n)ln2的时候，，最小错误率p等于(1/2) ^ k ≈ (0.6185) ^ (m/n)。另外，注意到p是位数组中某一位仍是0的概率e^(-kn/m)为1/2，表示应着bit数组中0和1各一半。换句话说，要想保持错误率低，最好让位数组有一半还空着。

最优数组大小

将上面得到的k=(m/n)ln2，带入到p的概率公式中，得到如下，

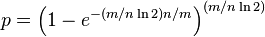
经过变形得到如下等式，

可以求得m，

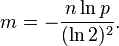
性能数据

下图显示了n，m和p之间的关系。

假设错误率在1%，那么当n等于1000000的时候，m为2M（内存大小）。当n等于100000000的时候，m为512M。随着数据量n的不断增加，想满足错误率在1%，所占的内存不断增加，而且不是线性增长，从100万增长到1亿时（100倍），内存从2M增长到了512M（256）。也就是说内存的消耗很可能随着n的增长成指数的增长。所以当数据量很大的时候，是否采用bloom filter需要认真的考虑。

下面的三个表显示了m/n ，k，p之间的关系。

Table 1: False positive rate under various m/n and k combinations.
m/n	k	k=1	k=2	k=3	k=4	k=5	k=6	k=7	k=8
2	1.39	0.393	0.400
3	2.08	0.283	0.237	0.253
4	2.77	0.221	0.155	0.147	0.160
5	3.46	0.181	0.109	0.092	0.092	0.101
6	4.16	0.154	0.0804	0.0609	0.0561	0.0578	0.0638
7	4.85	0.133	0.0618	0.0423	0.0359	0.0347	0.0364
8	5.55	0.118	0.0489	0.0306	0.024	0.0217	0.0216	0.0229
9	6.24	0.105	0.0397	0.0228	0.0166	0.0141	0.0133	0.0135	0.0145
10	6.93	0.0952	0.0329	0.0174	0.0118	0.00943	0.00844	0.00819	0.00846
11	7.62	0.0869	0.0276	0.0136	0.00864	0.0065	0.00552	0.00513	0.00509
12	8.32	0.08	0.0236	0.0108	0.00646	0.00459	0.00371	0.00329	0.00314
13	9.01	0.074	0.0203	0.00875	0.00492	0.00332	0.00255	0.00217	0.00199
14	9.7	0.0689	0.0177	0.00718	0.00381	0.00244	0.00179	0.00146	0.00129
15	10.4	0.0645	0.0156	0.00596	0.003	0.00183	0.00128	0.001	0.000852
16	11.1	0.0606	0.0138	0.005	0.00239	0.00139	0.000935	0.000702	0.000574
17	11.8	0.0571	0.0123	0.00423	0.00193	0.00107	0.000692	0.000499	0.000394
18	12.5	0.054	0.0111	0.00362	0.00158	0.000839	0.000519	0.00036	0.000275
19	13.2	0.0513	0.00998	0.00312	0.0013	0.000663	0.000394	0.000264	0.000194
20	13.9	0.0488	0.00906	0.0027	0.00108	0.00053	0.000303	0.000196	0.00014
21	14.6	0.0465	0.00825	0.00236	0.000905	0.000427	0.000236	0.000147	0.000101
22	15.2	0.0444	0.00755	0.00207	0.000764	0.000347	0.000185	0.000112	7.46e-05
23	15.9	0.0425	0.00694	0.00183	0.000649	0.000285	0.000147	8.56e-05	5.55e-05
24	16.6	0.0408	0.00639	0.00162	0.000555	0.000235	0.000117	6.63e-05	4.17e-05
25	17.3	0.0392	0.00591	0.00145	0.000478	0.000196	9.44e-05	5.18e-05	3.16e-05
26	18	0.0377	0.00548	0.00129	0.000413	0.000164	7.66e-05	4.08e-05	2.42e-05
27	18.7	0.0364	0.0051	0.00116	0.000359	0.000138	6.26e-05	3.24e-05	1.87e-05
28	19.4	0.0351	0.00475	0.00105	0.000314	0.000117	5.15e-05	2.59e-05	1.46e-05
29	20.1	0.0339	0.00444	0.000949	0.000276	9.96e-05	4.26e-05	2.09e-05	1.14e-05
30	20.8	0.0328	0.00416	0.000862	0.000243	8.53e-05	3.55e-05	1.69e-05	9.01e-06
31	21.5	0.0317	0.0039	0.000785	0.000215	7.33e-05	2.97e-05	1.38e-05	7.16e-06
32	22.2	0.0308	0.00367	0.000717	0.000191	6.33e-05	2.5e-05	1.13e-05	5.73e-06

Table 2: False positive rate under various m/n and k combinations.
m/n	k	k=9	k=10	k=11	k=12	k=13	k=14	k=15	k=16
11	7.62	0.00531
12	8.32	0.00317	0.00334
13	9.01	0.00194	0.00198	0.0021
14	9.7	0.00121	0.0012	0.00124
15	10.4	0.000775	0.000744	0.000747	0.000778
16	11.1	0.000505	0.00047	0.000459	0.000466	0.000488
17	11.8	0.000335	0.000302	0.000287	0.000284	0.000291
18	12.5	0.000226	0.000198	0.000183	0.000176	0.000176	0.000182
19	13.2	0.000155	0.000132	0.000118	0.000111	0.000109	0.00011	0.000114
20	13.9	0.000108	8.89e-05	7.77e-05	7.12e-05	6.79e-05	6.71e-05	6.84e-05
21	14.6	7.59e-05	6.09e-05	5.18e-05	4.63e-05	4.31e-05	4.17e-05	4.16e-05	4.27e-05
22	15.2	5.42e-05	4.23e-05	3.5e-05	3.05e-05	2.78e-05	2.63e-05	2.57e-05	2.59e-05
23	15.9	3.92e-05	2.97e-05	2.4e-05	2.04e-05	1.81e-05	1.68e-05	1.61e-05	1.59e-05
24	16.6	2.86e-05	2.11e-05	1.66e-05	1.38e-05	1.2e-05	1.08e-05	1.02e-05	9.87e-06
25	17.3	2.11e-05	1.52e-05	1.16e-05	9.42e-06	8.01e-06	7.1e-06	6.54e-06	6.22e-06
26	18	1.57e-05	1.1e-05	8.23e-06	6.52e-06	5.42e-06	4.7e-06	4.24e-06	3.96e-06
27	18.7	1.18e-05	8.07e-06	5.89e-06	4.56e-06	3.7e-06	3.15e-06	2.79e-06	2.55e-06
28	19.4	8.96e-06	5.97e-06	4.25e-06	3.22e-06	2.56e-06	2.13e-06	1.85e-06	1.66e-06
29	20.1	6.85e-06	4.45e-06	3.1e-06	2.29e-06	1.79e-06	1.46e-06	1.24e-06	1.09e-06
30	20.8	5.28e-06	3.35e-06	2.28e-06	1.65e-06	1.26e-06	1.01e-06	8.39e-06	7.26e-06
31	21.5	4.1e-06	2.54e-06	1.69e-06	1.2e-06	8.93e-07	7e-07	5.73e-07	4.87e-07
32	22.2	3.2e-06	1.94e-06	1.26e-06	8.74e-07	6.4e-07	4.92e-07	3.95e-07	3.3e-07

Table 3: False positive rate under various m/n and k combinations.
m/n	k	k=17	k=18	k=19	k=20	k=21	k=22	k=23	k=24
22	15.2	2.67e-05
23	15.9	1.61e-05
24	16.6	9.84e-06	1e-05
25	17.3	6.08e-06	6.11e-06	6.27e-06
26	18	3.81e-06	3.76e-06	3.8e-06	3.92e-06
27	18.7	2.41e-06	2.34e-06	2.33e-06	2.37e-06
28	19.4	1.54e-06	1.47e-06	1.44e-06	1.44e-06	1.48e-06
29	20.1	9.96e-07	9.35e-07	9.01e-07	8.89e-07	8.96e-07	9.21e-07
30	20.8	6.5e-07	6e-07	5.69e-07	5.54e-07	5.5e-07	5.58e-07
31	21.5	4.29e-07	3.89e-07	3.63e-07	3.48e-07	3.41e-07	3.41e-07	3.48e-07
32	22.2	2.85e-07	2.55e-07	2.34e-07	2.21e-07	2.13e-07	2.1e-07	2.12e-07	2.17e-07

关于Hash函数

有了前面的理论，那么剩下的重要的就是哈希函数如何设计了。K个哈希函数需要相互独立，如果做不到这点将使得错误率提升。而且K个哈希函数的实现不能占用过多的空间和时间，因为这会增加插入和查找的开销。 Less Hashing, Same Performance: Building a Better Bloom Filter一文中提到可以使用两个哈希函数H1和H2模拟出k个哈希函数，它的策略是hi = H1 + iH2，其中i从0到k-1.。这样做的好处是，不用可考虑k很大的时候哈希函数的设计，无论k如何变化，只需要设计出足够好的H1和H2就可以了。同时这样做可以简化计算量，只需要计算H1(X)和H2(X)，之后的Hi(X)都可以根据上面的计算结果得出。

实现

/**
 * implemention of Bloom Filter
 * @author lpmoon
 *
 */
public class BloomFilter {
	private double LN2 = Math.log(2);
	// the number of element
	private long n;
	// false positive
	private double p;
	// size of bit array
	private int m;
	// number of hash function
	private int k;
	// bit array
	private long bloomArray[];
	
	/**
	 * Constructor
	 * @param n
	 * @param p
	 */
	public BloomFilter(long n, double p) {
		this.n = n;
		this.p = p;
		this.m = getM();
		this.k = getK();
		bloomArray = new long[m / 4];
	}
	
	public boolean exist(String str){
		long hash1 = BKDRHash(str);
		long hash2 = APHash(str);

		for(int i = 0; i < this.k; ++i){
			long hashk = BloomHashK(hash1, hash2, i);
			
			//offset in int array
			long offsetInArray = hashk / 64;
			//offset in the element in position 'offsetInArray'
			long offsetInInt = 63 - (hashk % 64);

			long temp = 1 << offsetInInt;
			
			if ((bloomArray[(int) (offsetInArray % (m / 4))] & temp) == 0){
				return false;
			}
		}
		
		return true;
	}
	/**
	 * insert a new element into the bloom filter
	 * @param str
	 */
	public void insert(String str){
		long hash1 = BKDRHash(str);
		long hash2 = APHash(str);

		for(int i = 0; i < this.k; ++i){
			long hashk = BloomHashK(hash1, hash2, i);
			
			//offset in int array
			long offsetInArray = hashk / 64;
			//offset in the element in position 'offsetInArray'
			long offsetInInt = 63 - (hashk % 64);

			long temp = 1 << offsetInInt;
			
			bloomArray[(int) (offsetInArray % (m / 4))] |= temp;
		}
	}
	
	/**
	 * Get the number of hash function
	 * k = (m / n) * ln2
	 * @return
	 */
	private int getK(){
		return (int) ((m / n) * LN2);
	}
	/**
	 * Get the size of bit array
	 * m = (- nlnp)/((ln2)^2)
	 * @return
	 */
	private int getM(){
		return (int) ((-n * Math.log(p)) / (LN2 * LN2));
	}
	
	/**
	 * get the hash of the k'th hash function
	 * @param hash1
	 * @param hash2
	 * @param k
	 * @return
	 */
	private long BloomHashK(long hash1, long hash2, int k){
		return hash1 + k * hash2;
	}
	
	/**
	 * BKDR hash algorithm
	 * @param str
	 * @return
	 */
	private long BKDRHash(String str){
		long seed = 131;
		long hash = 0;
		for (int i = 0; i < str.length(); ++i){
			hash = (hash * seed) + str.charAt(i);
		}
		
		return hash;
	}
	
	/**
	 * AP hash algorithm
	 * @param str
	 * @return
	 */
	private long APHash(String str){
		long hash = 0xAAAAAAAA;
		for (int i = 0; i < str.length(); i++){
			if ((i & 1) == 0){
				hash ^= ((hash << 7) ^ str.charAt(i) * (hash >> 3));
			}
			else{
				hash ^= (~((hash << 11) + str.charAt(i) ^ (hash >> 5)));
			}
		}
		
		return hash;
	}
	public static void main(String[] args) {
		BloomFilter bf = new BloomFilter(10, 0.01);
		String[] eles = {"aa", "bb", "cc", "dd", "ee", "ff", "gg", "hh", "ii", "jj"};
		for (String ele : eles){
			bf.insert(ele);
		}
		for (String ele : eles){
			System.out.println(bf.exist(ele));
		}
		
		System.out.println(bf.exist("fg"));
		System.out.println(bf.exist("fg2"));
		System.out.println(bf.exist("ddee"));
	}
}

应用举例

像网易，QQ这样的公众电子邮件（email）提供商，总是需要过滤来自发送垃圾邮件的人（spamer）的垃圾邮件。

一个办法就是记录下那些发垃圾邮件的 email 地址。由于那些发送者不停地在注册新的地址，全世界少说也有几十亿个发垃圾邮件的地址，将他们都存起来则需要大量的网络服务器。

如果用哈希表，每存储一亿个 email 地址，就需要 1.6GB 的内存（用哈希表实现的具体办法是将每一个 email 地址对应成一个八字节的信息指纹，然后将这些信息指纹存入哈希表，由于哈希表的存储效率一般只有 50%，因此一个 email 地址需要占用十六个字节。一亿个地址大约要 1.6GB，即十六亿字节的内存）。因此存贮几十亿个邮件地址可能需要上百 GB 的内存。

而Bloom Filter只需要哈希表 1/8 到 1/4 的大小就能解决同样的问题。

Bloom Filter决不会漏掉任何一个在黑名单中的可疑地址。而至于误判问题，常见的补救办法是在建立一个小的白名单，存储那些可能别误判的邮件地址。