数据结构 二叉树

一：二叉树
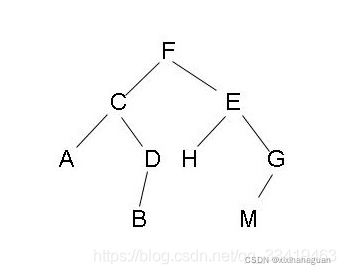
二叉树是一种数据结构，其每个结点最多有两个子树的树结构。也就是每个节点下面有两个分叉，通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

最上面的节点称为根节点，相对最下面的节点称之为叶节点。

一棵深度为k，且有2^k-1个节点的二叉树，称为满二叉树。这种树的特点是每一层上的节点数都是最大节点数。而在一棵二叉树中，除最后一层外，若其余层都是满的，并且最后一层或者是满的，或者是在右边缺少连续若干节点，则此二叉树为完全二叉树。具有n个节点的完全二叉树的深度为floor(log2n)+1。深度为k的完全二叉树，至少有2k-1个叶子节点，至多有2k-1个节点。

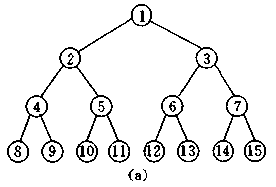
二：满二叉树
除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树

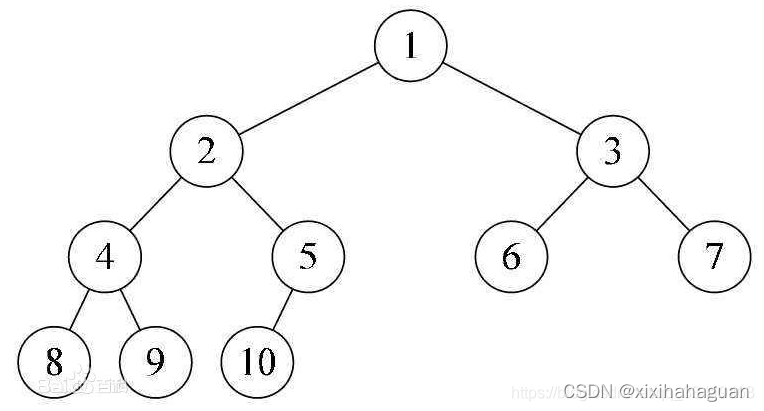
三：完全二叉树
完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。

若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树

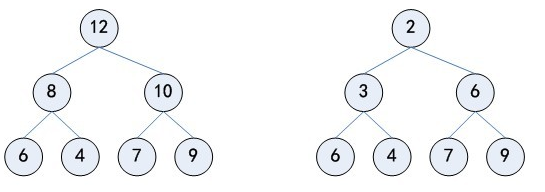
四：堆
当一颗二叉树的每个结点都大于等于它的两个子节点时，它被称为堆有序。相应地，在堆有序的二叉树中，每个结点都小于等于它的父节点，从任意结点往上，我们都能得到一列非递减的元素；从任意结点往下，我们都能得到一列非递增的元素。根节点就是堆有序的二叉树中的最大节点。所以说在一个堆有序的二叉树中，父节点的位置是K/2,它的两个子节点的位置是2k,2k+1。这样通过索引的变化，我们就可以在数组中得到不同的元素了