数据结构笔记（七）——左式堆/左偏树（leftist heap）（2）

最新推荐文章于 2024-01-14 12:12:39 发布

原创最新推荐文章于 2024-01-14 12:12:39 发布 · 560 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #C/C++

数据结构专栏收录该内容

15 篇文章

订阅专栏

本文介绍了一种高效的数据结构——左式堆，用于实现优先队列。左式堆通过特殊的二叉树结构和零路径长属性，使得合并操作能在O(logN)时间内完成，优于传统的二叉堆。文章详细解释了左式堆的特性、合并操作的原理及其实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前面二叉堆实现了优先队列基本的插入和删除最小元操作，但如果想要将两个堆合并的话就不太容易了，我们要把一个数组里的数据拷贝到另一个数组，如果数组1和数组2大小相同，那么合并操作的时间就是O（N）。果然合并还是需要指针呀，所以我们提出了左式堆，但是注意指针操作实际会比乘除运算更加耗费时间。

左式堆（Leftist Heap）也有结构和有序性。左式堆的有序性和二叉堆一样，父亲小于所有的儿子。它不再是用数组实现，而是采用二叉树。先定义一个零路径长（null path length，npl）：npl（x）定义为从节点x到一个没有两个儿子的节点的最短路径长。左式堆在结构上要满足：对于每个节点X，其左儿子的零路径长大于等于右儿子的零路径长。这个性质让树倾向于向左偏，所以也叫左偏树。

由左式堆的结构性，我们可以得到npl（x）=min（npl（LeftChild），npl（RightChild））+1

而对任意节点，npl（LeftChild） $\geq$ npl（RightChild）

所以 npl（x）=npl（RightChild）+1，这个在merge合并时更新npl就可以用到了。

左式堆右边比左边浅，合并操作只涉及到右边使算法效率提高。可以证明：在右路径上有r个节点的左式树必然至少有 $2^{_{r}}$ +1个节点，进一步我们知道N个节点的左式堆有一条右路径最多含有abs（log（N+1））个节点，那么合并操作就可以被控制在O（logN）。

左式堆的合并操作：不断把最小值大的堆和最小值小的堆的右子树合并，比较左右的npl，把npl大的交换到左边，时间界为log（N）。举个例子（逆时针从左往右看）

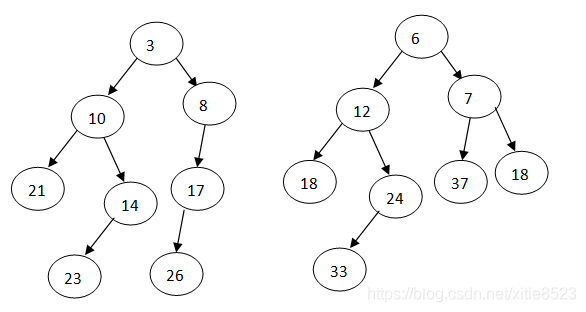
堆H1 堆H2 结果

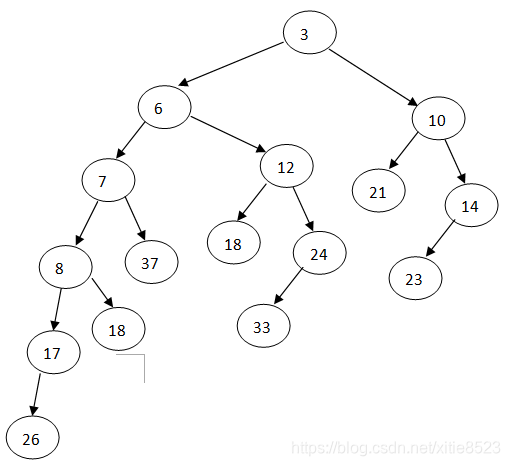
H1->right和H2合并，放到H1->right处，以此类推

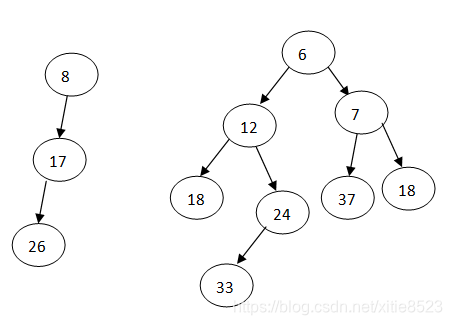
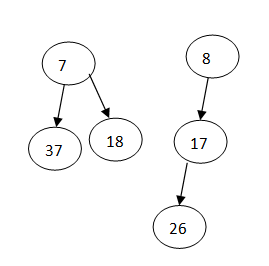
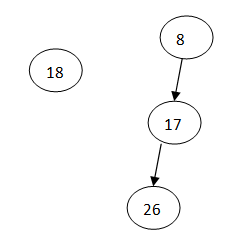合并——》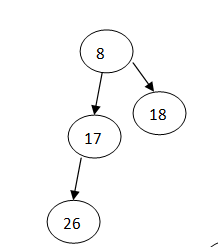

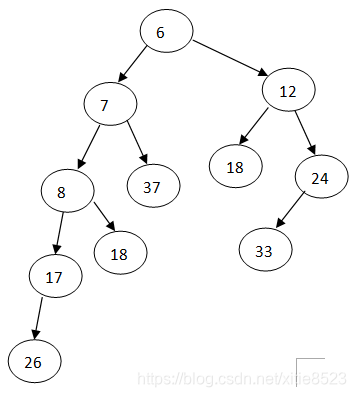
插入操作只要把插入节点看成一个堆，用合并可以完成插入的操作；删除最小元只需要删掉根节点，然后把左子树和右子树合并起来，时间界都为log（N）。buildHeap可以多次插入，这种方法比较耗时，更快速的方法是借助队列。将所有元素放入队列中，把这些节点都看成左式堆，前两个元素出队合并为一个堆再入队（放在队列最后面），依此操作下去。

代码：

LeftHeap.h

#pragma once
#include<iostream>
using namespace std;
typedef int ElementType;
struct TreeNode;
typedef TreeNode *Position;
typedef Position LeftHeap;
LeftHeap initialize();
LeftHeap buildHeap(LeftHeap h);
bool isEmpty(LeftHeap h);
LeftHeap merge(LeftHeap h1, LeftHeap h2);
ElementType findMin(LeftHeap h);
#define insert(h,x) (h=insert1((h),(x)))
LeftHeap insert1(LeftHeap h, ElementType e);
LeftHeap deleteMin1(LeftHeap h);
void destory(LeftHeap h);
void printHeap(LeftHeap h);
struct TreeNode
{
	ElementType element;
	Position left;
	Position right;
	int npl;
};

LeftHeap.cpp

#include "stdafx.h"
#include "LeftHeap.h"
LeftHeap initialize()
{
	return nullptr;
}
LeftHeap buildHeap(LeftHeap h)
{
	ElementType input;
	cout << "input: " << endl;
	cin >> input;
	while (input!=-1)
	{
		insert(h, input);
		cin >> input;
	}
	return h;
}
bool isEmpty(LeftHeap h)
{
	return h == nullptr;
}
void swapChild(LeftHeap h)
{
	Position tmp = h->left;
	h->left = h->right;
	h->right = tmp;
}
LeftHeap merge1(LeftHeap h1, LeftHeap h2)
{
	if (h1->left==nullptr)
	{
		h1->left = h2;
	}
	else
	{
		h1->right = merge(h1->right, h2);
		if (h1->left->npl < h1->right->npl)
		{
			swapChild(h1);
		}
		h1->npl = h1->right->npl + 1;
	} 
	return h1;
}
LeftHeap merge(LeftHeap h1, LeftHeap h2)
{
	if (h1==nullptr)
	{
		return h2;
	}
	if (h2==nullptr)
	{
		return h1;
	}
	if (h1->element<h2->element)
	{
		return merge1(h1, h2);
	}
	else
	{
		return merge1(h2, h1);
	}
}

LeftHeap insert1(LeftHeap h, ElementType e)
{
	Position node = (Position)malloc(sizeof(TreeNode));
	if (node==nullptr)
	{
		cerr << "out of space" << endl;
	}
	else
	{
		node->left = nullptr;
		node->right = nullptr;
		node->element = e;
		node->npl = 0;
		h = merge(h, node);
	}
	return h;
}
ElementType findMin(LeftHeap h)
{
	if (!isEmpty(h))
	{
		return h->element; 
	}
	cerr << "heap is empty" << endl;
	return 0;
}
LeftHeap deleteMin1(LeftHeap h)
{
	if (isEmpty(h))
	{
		cerr << "heap is empty" << endl;
		return h;
	}
	LeftHeap leftchild = h->left;
	LeftHeap rightchild = h->right;
	free(h);
	return merge(leftchild, rightchild);
}

void destory(LeftHeap h)
{
	if (isEmpty(h))
	{
		return;
	}
	destory(h->left);
	destory(h->right);
	free(h);
	h = nullptr;
}
void printHeap(LeftHeap h)
{
	if (!isEmpty(h))
	{
		cout << h->element << " ";
		printHeap(h->left);
		printHeap(h->right);
	}
}

test.cpp


#include "stdafx.h"
#include "LeftHeap.h"
int main()
{
	LeftHeap heap = initialize();
	heap = buildHeap(heap);
	printHeap(heap);
	cout << endl;
	heap=deleteMin1(heap);
	printHeap(heap);
	cout << endl;
	destory(heap);
    return 0;
}

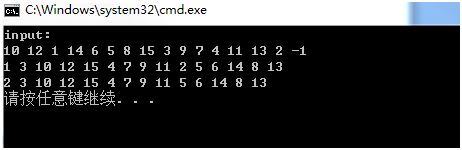
结果：