【CTF】【Crypto】 ECC 小计

【CTF】【Crypto】 ECC 小计

ECC原理

ecc是离散对数问题，看这个：https://ctf-wiki.org/crypto/asymmetric/discrete-log/ecc/
白话：假设有一个点P，整数 k，kP = Q，

• 已知k求Q好求
• 已知PQ，求k比较难求。

关键运算

kP怎么求？

看这个http://www.aqtd.com/nd.jsp?id=1682
白话：2P = P + P, 3P = P + 2P转化为点加运算，分两种情况
相同点和不同点
公式：

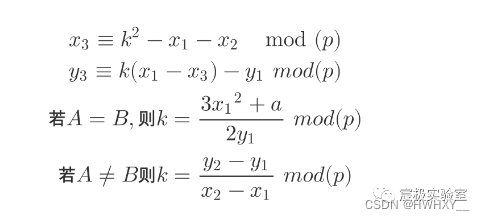
运算实现

python3脚本

def add(A,B,M):
    if A==(0,0): return B
    if B==(0,0): return A
    x1,y1 = A
    x2,y2 = B
    if A!=B:
        p = (y2-y1)*pow(x2-x1,M-2,M)
    else:
        p = (3*x1*x1+a)*pow(2*y1,M-2,M)
    x3 = p*p-x1-x2
    y3 = p*(x1-x3)-y1
    return (x3%M,y3%M)

工具

在线sage运算：https://sagecell.sagemath.org/
比较常用的就是构建椭圆曲线，然后封装了一些点的运算。实现方式参考wiki上照猫画虎
https://github.com/sonickun/ctf-crypto-writeups/blob/master/2013/seccon-ctf-quals/cryptanalysis/solver.sage.py