20 OpenCV霍夫圆变换HoughCircles

一、霍夫圆检测原理

• 对直线来说, 一条直线能由参数极径极角 (r,θ) 表示.
  而对圆来说, 从平面坐标到极坐标转换需要三个参数, 也就是： ( x_center , y_center, r )。其中x_center , y_center 表示圆心，r 表示圆的半径。这就意味着需要大量的内存而且执行效率会很低，速度会很慢。
  
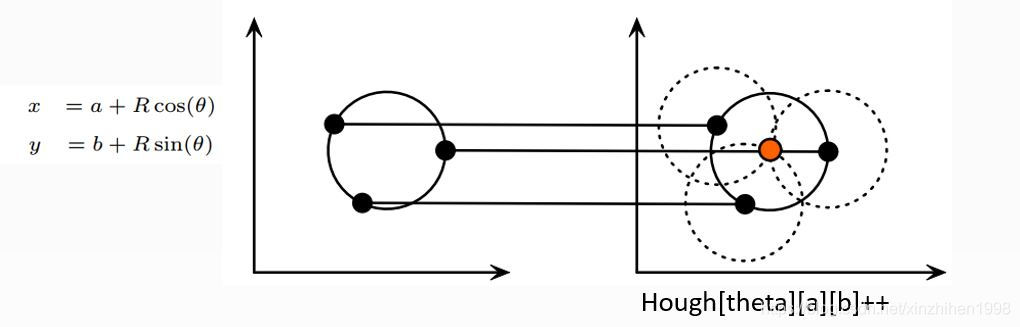
• 霍夫圆检测对噪声比较敏感，所以首先要对图像做中值滤波
• 为了提高效率，OpenCV实现了一种比标准Hough变换稍微复杂的检测方法：Hough梯度方法，它由两个主要阶段组成。
  第一阶段：检测边缘，发现可能的圆心
  第二阶段：基于第一步的基础上从候选圆心开始计算最佳半径大小

二、霍夫梯度法

• 原理

【1】首先对图像应用边缘检测，比如用canny边缘检测。

【2】然后，对边缘图像中的每一个非零点，考虑其局部梯度，即用Sobel（）函数计算x和y方向的Sobel一阶导数得到梯度。

【3】利用得到的梯度，由斜率指定的直线上的每一个点都在累加器中被累加，这里的斜率是从一个指定的最小值到指定的最大值的距离。

【4】同时，标记边缘图像中每一个非0像素的位置。

【5】然后从二维累加器中这些点中选择候选的中心，这些中心都大于给定阈值并且大于其所有近邻。这些候选的中心按照累加值降序排列，以便于最支持像素的中心首先出现。

【6】接下来对每一个中心，考虑所有的非0像素。

【7】这些像素按照其与中心的距离排序。从到最大半径的最小距离算起，选择非0像素最支持的一条半径。

【8】如果一个中心收到边缘图像非0像素最充分的支持，并且到前期被选择的中心有足够的距离，那么它就会被保留下来。

这个实现可以使算法执行起来更高效，或许更加重要的是，能够帮助解决三维累加器中会产生许多噪声并且使得结果不稳定的稀疏分布问题。

• 缺点

<1>在霍夫梯度法中，我们使用Sobel导数来计算局部梯度，那么随之而来的假设是，其可以视作等同于一条局部切线，并这个不是一个数值稳定的做法。在大多数情况下，这样做会得到正确的结果，但或许会在输出中产生一些噪声。

<2>在边缘图像中的整个非0像素集被看做每个中心的候选部分。因此，如果把累加器的阈值设置偏低，算法将要消耗比较长的时间。第三，因为每一个中心只选择一个圆，如果有同心圆，就只能选择其中的一个。

<3>因为中心是按照其关联的累加器值的升序排列的，并且如果新的中心过于接近之前已经接受的中心的话，就不会被保留下来。且当有许多同心圆或者是近似的同心圆时，霍夫梯度法的倾向是保留最大的一个圆。可以说这是一种比较极端的做法，因为在这里默认Sobel导数会产生噪声，若是对于无穷分辨率的平滑图像而言的话，这才是必须的。

三、HoughCircles

void cv::HoughCircles   (   InputArray      image,
        OutputArray     circles,
        int     method,
        double      dp,
        double      minDist,
        double      param1 = 100