树和二叉树

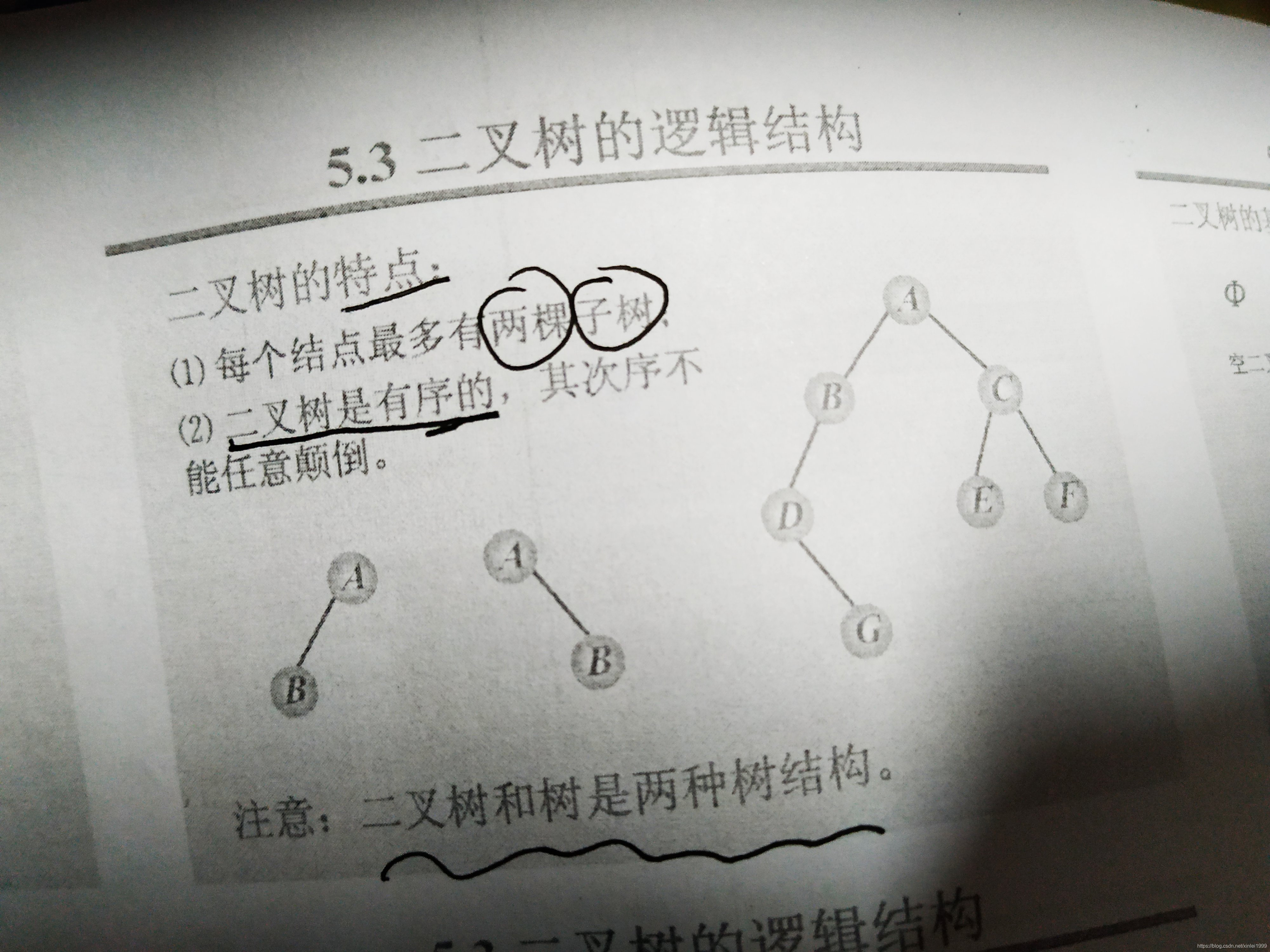
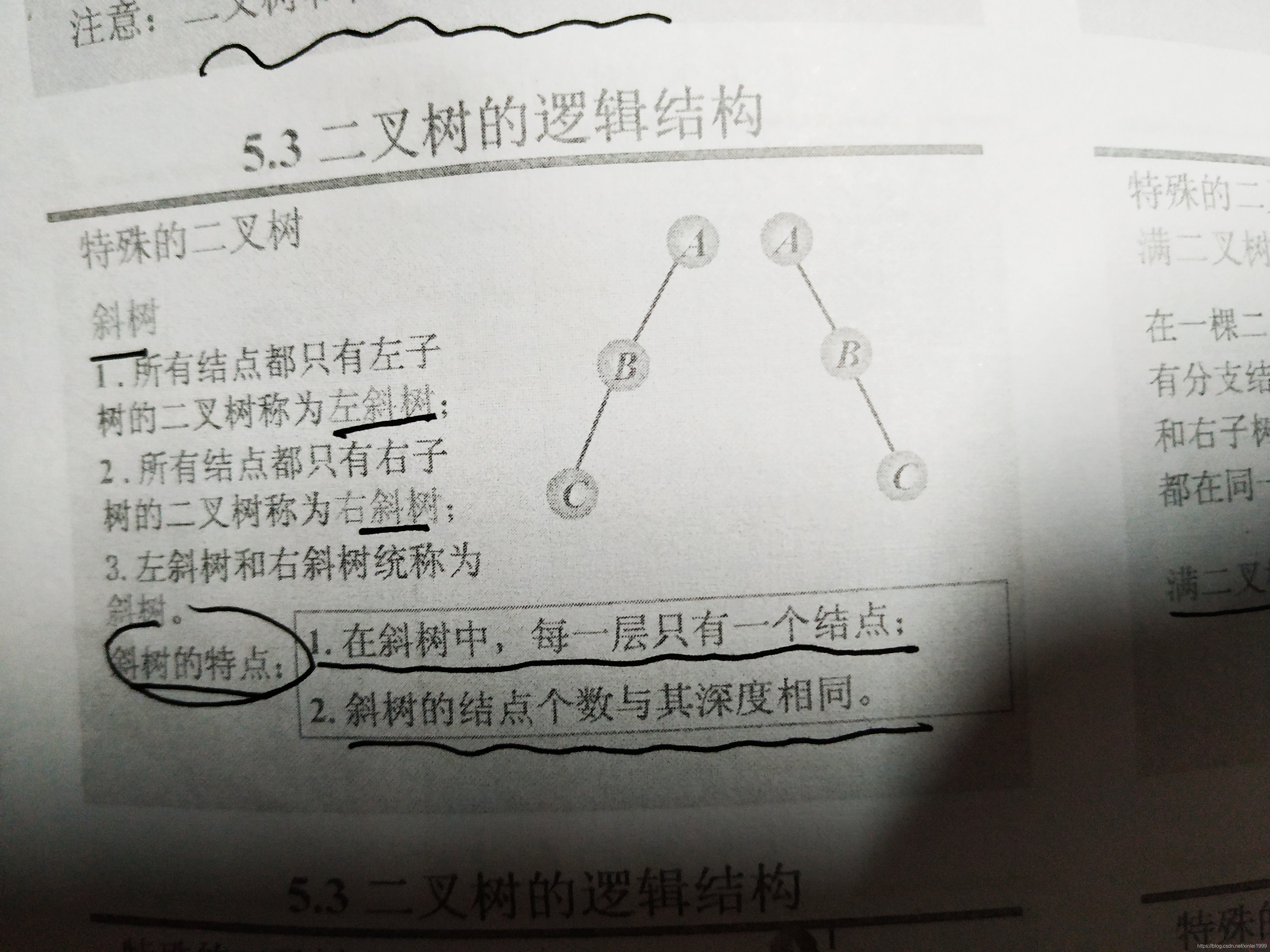
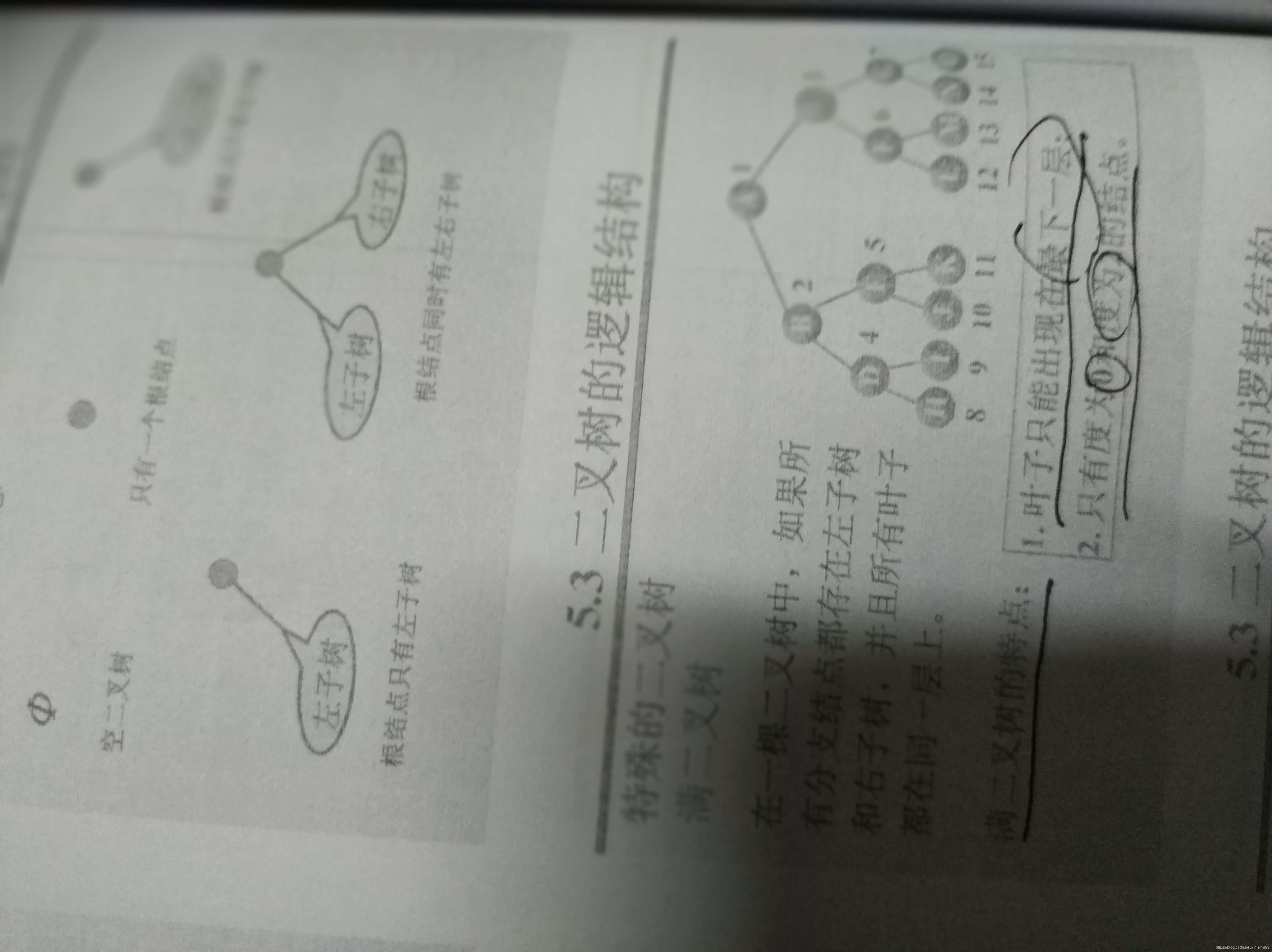
一、基本性质：

1. 在二叉树中，第i层的结点总数不超过2^(i-1)；
2. 深度为h的二叉树最多有2^h-1个结点(h>=1)，最少有h个结点；
3. 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1；
4. 具有n个结点的完全二叉树的深度为int（log2n）+1
   5）给定N个节点，能构成h(N)种不同的二叉树。h(N)为卡特兰数的第N项。h(n)=C(n,2*n)/(n+1)。
   二、什么是完全二叉树？

若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层有叶子结点，并且叶子结点都是从左到右依次排布。
三、什么是满二叉树？

除了叶结点外每一个结点都有左右子结点且叶子结点都处在最底层的二叉树。
四、存储方式

存储的方式和图一样，有链表和数组两种，用数组存访问速度快，但插入、删除节点操作就比较费时了。实际中更多的是用链来表示二叉树的。