河内之塔
题目说明:
创世纪时,Benares有一座波罗教塔,是由三只钻石棒所支撑,开始时神在第一根棒子上放置了64个由上至下 依小到大的排列的金盘,并命令僧侣将所有的金盘从第一根石棒移至第三根石棒,且搬运过程中遵守大盘子在小盘子的下面的原则。若每日仅搬一个盘子,则当盘子全数搬完时,此塔将会损毁,也就是世界末日来临之时。
算法思路:
如果柱子标为ABC,要由A搬至C,在只有一个盘子时,就将它搬至C,当有两个盘子,就将它当做辅助。
如果盘子超过2个,将第三个一下的盘子遮住,就简单了。
每次处理两个盘子,也就是 A->B,A->C,B->C这三个步骤,被遮住的部分。就进入递归处理。
程序代码:
#include <stdio.h> void hanoi(int n,char A,char B,char C) { if(n==1) { printf("Move sheet %d from %c to %c\n",n,A,C); } else { hanoi(n-1,A,C,B); printf("Move sheet %d from %c to %c.",n,A,C); hanoi(n-1,B,A,C); } } int main() { int n; printf("请输入盘数:"); scanf("%d",&n); hanoi(n,'A','B','C'); return 0; }
运行结果:
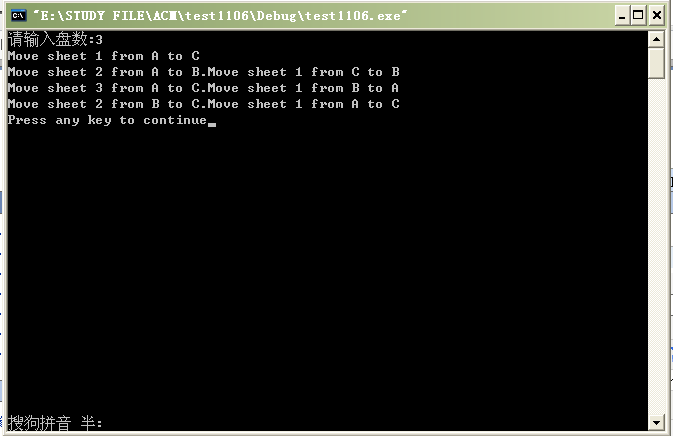







 本文介绍了河内之塔问题的背景及递归算法实现。该问题起源于创世纪时期的传说,涉及将64个不同大小的金盘从一根柱子移动到另一根柱子上,同时遵循大盘在小盘下方的规则。文中提供了C语言实现的递归解决方案。
本文介绍了河内之塔问题的背景及递归算法实现。该问题起源于创世纪时期的传说,涉及将64个不同大小的金盘从一根柱子移动到另一根柱子上,同时遵循大盘在小盘下方的规则。文中提供了C语言实现的递归解决方案。
















 3889
3889

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








