数据结构实验——基于广度优先搜索的六度空间理论验证

前言

这道实验核心是写bfs（广度优先搜索），bfs的算法如果有缘的话我会令开一篇博客去解释。

我的bfs代码风格是两层套，这样才能给每次的bfs加上层级。但是每个人的代码风格不可能完全一致，所以仅供参考，想认真学习算法的同学建议写出自己的bfs来。

实验实习过程步骤（注意是主要关键步骤，不是所有步骤，适当文字+截图说明）

手撕BFS，那咋了！

要搞清楚这题怎么做，那搞懂BFS算法的流程是第一步。

BFS广度优先搜索和DFS深度优先搜索都是图论中的内容，但是好像DFS在算法竞赛更常用，一条路递归走到底再回来。就是“深度”问题。而“广度”，则是一层一层往下走，逐层深入。这样就带来了一个问题：我怎么知道哪一层有哪些数？这个问题在学数据结构前（因为之前接触过）困扰了我许久。

图来自：广度优先搜索BFS-优快云博客

然后老师提到了一个词：队列。然后我就顿悟了一般，你如果单纯靠for循环走肯定是无记忆的，需要把每层的结点挪到一个队列里面，你才能知道啥时候开始啥时候结束。上面这图优快云讲BFS的图，队列就是白色的矩形。

但是思考一下，对于不同的层，我怎么知道分界线在哪里？

为什么需要讨论分界线，实际上是因为题目的要求，这题的六度空间，实质是需要知道6层关系之内的人占比，所以不同层级一定要界线，我在这里采用了times作为深度，对于一张连通图，times每一层的times加1，而非连通图，times就＋99（超过6就行）。然后每个人的深度都用一个depth[]数组存放，那么，该人的depth与其他人的depth小于6占所有人的占比，就是所求的答案。

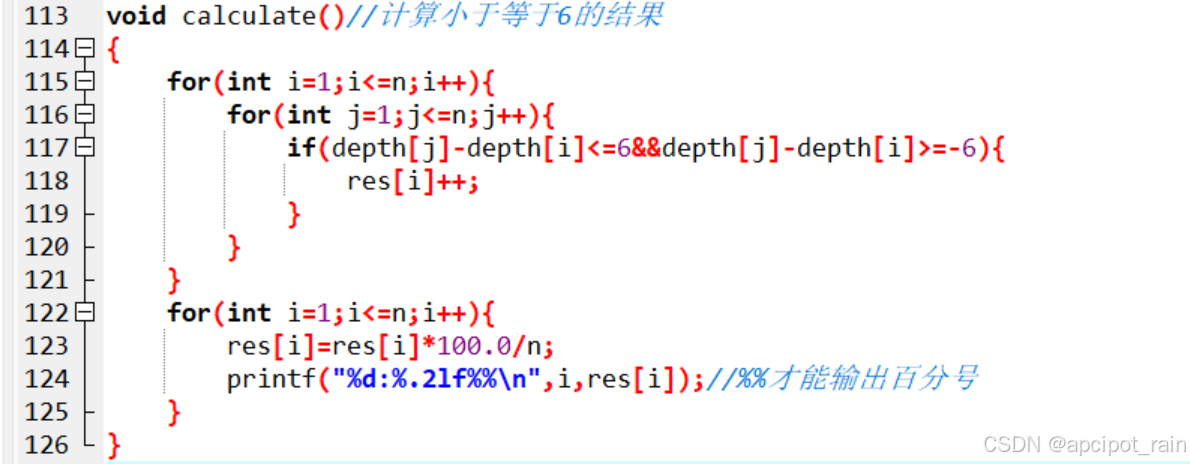
知道为什么要分界线，那么这张队列我实际上可以用0作为结尾分界线，记得读入0后0也要出队就行了，我第一次调试失败就在这里。

以上是顶层核心设计，然后下面完善BFS实际上也不简单，我在这里采用了三套循环。第一套循环是所有的非连通图分隔开搜索循环，第二套循环是对于同一张连通图，不同层次之间递进搜索循环，第三套就是同一层次不同元素的搜索。那么显然，0结尾队列分界线在第二层循环里面实现，非连通图的times+99在第一层循环里实现。

再下面就是队列的操作函数了，记得是数组实现队列。至于邻接矩阵，我都搬用的上题的代码。。。

实验实习结果及分析

不仅符合描述的测试点（如图），而且对于其他测试点也能过。

实验遇到的问题及解决办法，实验心得体会及对此实验的意见或建议（有就写，无可不写）

算法代码的实现确实是一个逐步积累的过程，很苦但是坚持下去就会有收获，不停地盘算代码实现逻辑，不断修改，才能真正练好代码能力。

搬运工有话说

突然想起来，我这题用了GPT给队列，如果你们去解锁C++技能，就能直接用队列库啦！

Code:

刚说了想认真学习算法的同学建议写出自己的bfs来！

我的bfs挖掉了第二个函数的判断条件，会填了就算理解了我的双层循环的精髓了。

#include<stdio.h>
#define M 10086	//无穷远 

int n,m;			//问题规模
int temp1,temp2;	//朋友 
int G[105][105]={0};//邻接矩阵 
int queue[105]={0};	//队列，装每一轮的情况 
int status[105]={0};//是否被搜索到 
int depth[105]={0};	//深度位置 
int times = 1;			//入栈次数 
int front = 1,rear = 1;// 队头指针，队尾指针
double res[105]={0};	//到位距离，是否小于6，输出结果 

void initG();	//初始化图 
void input();	//繁琐的输入函数
void bfs();		//广度优先搜索 
void calculate();//计算小于等于6的结果 
//队列操作
int isEmpty(); 
int isFull();
void push(int value);
int pop();
int frontElement();
void printQueue();

int main()
{
	input();//输入数据 
	bfs();
	calculate();
	return 0;
}

void initG()//初始化图
{
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			G[i][j] = M;
		}
	}
}

void input()//繁琐的输入函数 
{
	scanf("%d %d",&n,&m);
	
	initG();//要先输入n才能初始图 
	
	for(int i=1;i<=m;i++){
		scanf("%d %d",&temp1,&temp2);
		G[temp1][temp2]=1;//行指向列 
		G[temp2][temp1]=1;//列指向行 
	}
	
	printf("邻接矩阵如下：\n");
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			printf("%5d ",G[i][j]);
		}
		printf("\n"); 
	}
	return ;
}

void bfs()//开始广搜 
{
	int pos=0;//位置 
	while(1){
		int flag=1;//整个循环结束标志 
		for(int i=1;i<=n;i++){
			if(status[i]==0){//没有被搜索过的节点当做图的开始 
				pos=i;//起始位置赋过去 
				push(pos);//找到开头的栈
				push(0); //输入0 
				status[i]=1;//已被搜索 
				depth[i]=times++;
				flag=0; //flag置0表示有连通图没被搜完 
				break;//找到一个就要结束 
			}
		} 
		
		if(flag) break;//flag不是0说明全部搜索完毕 
		
		//对于一张连通图的搜索 
		while(frontElement())//只要队列开头不是0，因为当且仅当没有新东西了队列才是0 
		{
			printQueue();//显示队列所有元素 
			int x=frontElement(); 
			pop();
			while(？？？)//同一层的搜索 入队 出队
			{
				for(int i=1;i<=n;i++){
					if(G[x][i]<M&&status[i]==0)//有通路而且未被搜 
					{	
						status[i]=1;//已经被搜到 
						depth[i]=times; 
						push(i); //压入栈 
					}  
				}
				x=frontElement();//开始数据，对于同一层次 
				pop();//顶出队 
			}
			push(0);//最后压入0 
			times++;//深度加1 
			
		}
		pop();//把队列尾巴的0给踢掉 
		times+=99;//非连通图，间隔100人 
	}
	return ; 
}

void calculate()//计算小于等于6的结果 
{
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(depth[j]-depth[i]<=6&&depth[j]-depth[i]>=-6)
			{
				res[i]++;
			}
		} 
	} 
	for(int i=1;i<=n;i++){
		res[i]=res[i]*100.0/n;
		printf("%d:%.2lf%%\n",i,res[i]);//%%才能输出百分号 
	} 
}

// 判断队列是否为空
int isEmpty() {
    return front == rear;
}

// 判断队列是否满
int isFull() {
    return rear == 104;
}

// 入队操作（向队列添加一个元素）
void push(int value) {
    if (isFull()) {
        printf("Queue is full!\n");
        return;
    }
    queue[rear] = value;  // 将值添加到队尾
    rear++;               // 更新队尾指针
}

// 出队操作（从队列移除队头元素）
int pop() {
    if (isEmpty()) {
        printf("Queue is empty!\n");
        return -1;  // 返回 -1 表示队列为空
    }
    int value = queue[front];  // 获取队头元素
    front++;  // 更新队头指针
    return value;
}

// 获取队头元素
int frontElement() {
    if (isEmpty()) {
        printf("Queue is empty!\n");
        return -1;  // 返回 -1 表示队列为空
    }
    return queue[front];
}

// 打印队列中的元素
void printQueue() {
    if (isEmpty()) {
        printf("Queue is empty!\n");
        return;
    }
    printf("队列如下: ");
    for (int i = front; i < rear; i++) {
        printf("%d ", queue[i]);
    }
    printf("\n");
}

10 9
1 2 
2 3 
3 4 
4 5 
5 6
6 7 
7 8 
8 9
9 10

10 8 
1 2 
2 3 
3 4 
4 5 
5 6
6 7 
7 8 
9 10

12 12
1 2
2 3
3 4
4 5
5 6
6 1
2 5
6 7
8 9
9 10
10 8
11 12