LeetCode刷题笔记
- 1. 基础数据结构
- 2. 二叉树
- 3. 动态规划
- [509] 斐波那契数
- [322] 零钱兑换
- [931] 下降路径最小和
- [300] 最长递增子序列
- [53] 最大子数组和
- [1143] 最长公共子序列
- [583] 两个字符串的删除操作
- [712] 两个字符串的最小ASCII删除和
- [72] 编辑距离
- [10] 正则表达式匹配
- 0-1背包问题
- [416] 分割等和子集
- [518] 零钱兑换 II
- [121] 买卖股票的最佳时机
- [122] 买卖股票的最佳时机 II
- [123] 买卖股票的最佳时机 III
- [188] 买卖股票的最佳时机 IV
- [309] 最佳买卖股票时机含冷冻期
- [714] 买卖股票的最佳时机含手续费
- [198] 打家劫舍
- [213] 打家劫舍 II
- [337] 打家劫舍 III
- [64] 最小路径和
- [887] 鸡蛋掉落
- 回文串
- 651. 四键键盘
- [312] 戳气球
- 3.1 贪心算法
- 4. 回溯算法
- 5. 高频
1. 基础数据结构
1.1 数组和链表
1. 前缀和数组
303. 区域和检索 - 数组不可变(中等)

- 题解
class NumArray {
//注释的方法不使用前缀和,直接进行区间的累加
// int[] nums;
// public NumArray(int[] nums) {
// this.nums = nums;
// }
// public int sumRange(int left, int right) {
// int res = 0;
// for (int i = left; i <= right; i++) {
// res+=nums[i];
// }
// return res;
// }
//前缀和的方法,利用一个数组进行记录由小到大区间内的数组和
int[] preSum;
public NumArray(int[] nums) {
preSum = new int[nums.length+1];
for (int i = 1; i < preSum.length; i++) {
preSum[i]+=preSum[i-1]+nums[i-1];
}
}
public int sumRange(int left, int right) {
return preSum[right+1] - preSum[left];
}
}
560. 和为K的⼦数组(中等)

- 题解
class Solution {
public int subarraySum(int[] nums, int k) {
//核心思想:利用Map记录前缀和出现的次数
HashMap<Integer,Integer> preSum = new HashMap<>();
//basecase
preSum.put(0, 1);
int res = 0, sum_i = 0;
for(int i = 0; i < nums.length; i++){
sum_i += nums[i];
//我们想要的前缀和
int sum_j = sum_i - k;
//存在该前缀和则进行更新
if(preSum.containsKey(sum_j)){
res += preSum.get(sum_j);
}
preSum.put(sum_i, preSum.getOrDefault(sum_i,0)+1);
}
return res;
}
}
2. 差分数组
370. 区间加法

- 题解
class Solution {
public int[] getModifiedArray(int length, int[][] updates) {
int[] nums = new int[length];
Difference diff = new Difference(nums);
for(int[] update : updates){
int i = update[0];
int j = update[1];
int val = update[2];
diff.increment(i, j, val);
}
return diff.result();
}
class Difference{
//差分数组
private int[] diff;
public Difference(int[] nums){
assert nums.length > 0;
//构造差分数组
diff = new int[nums.length];
diff[0] = nums[0];
for(int i = 1; i < nums.length; i++){
diff[i] = nums[i] - nums[i-1];
}
}
//区间增加val
public void increment(int i, int j, int val){
diff[i] += val;
if(j + 1 < diff.length){
diff[j + 1] -= val;
}
}
//构造结果数组
public int[] result(){
int[] res = new int[diff.length];
res[0] = diff[0];
for(int i = 1; i < diff.length; i++){
res[i] = diff[i] + res[i-1];
}
return res;
}
}
}
[1109] 航班预订统计
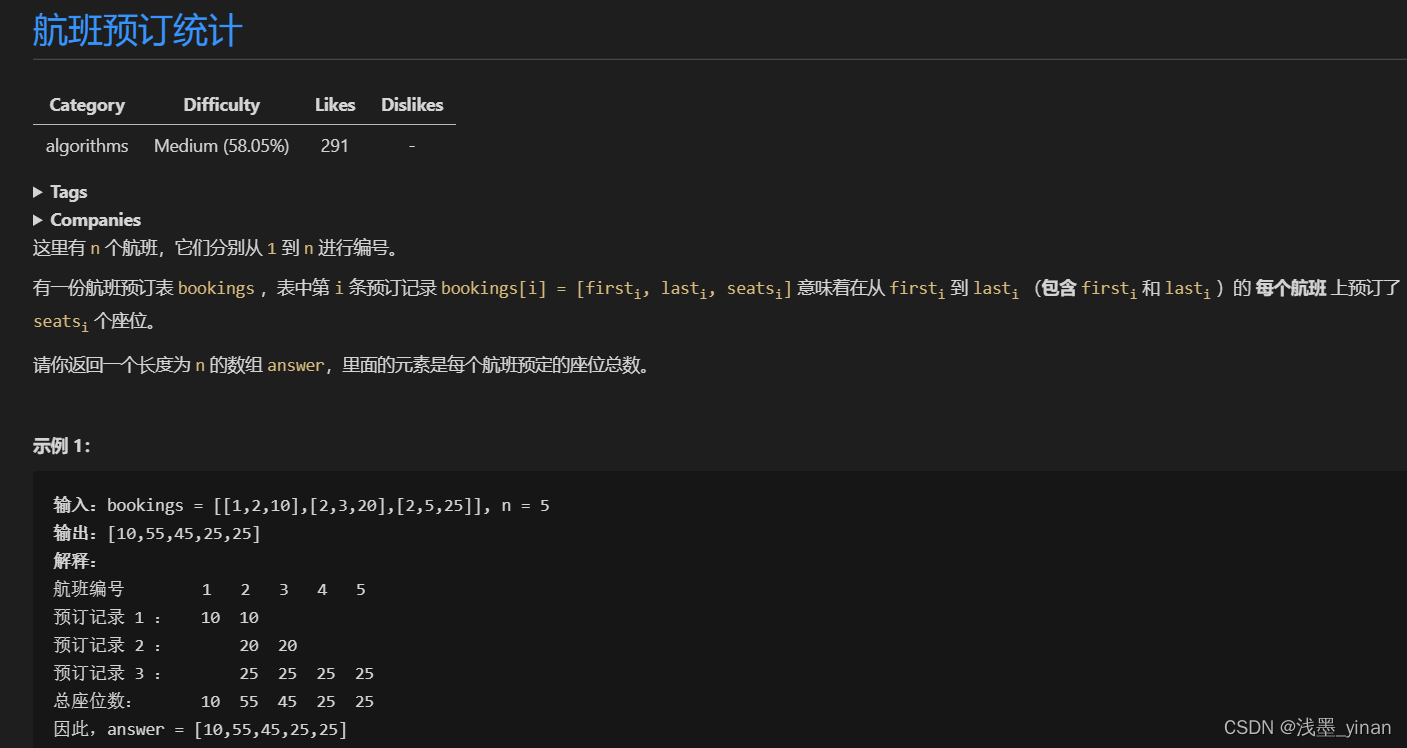
- 题解
class Solution {
public int[] corpFlightBookings(int[][] bookings, int n) {
int[] res = new int[n];
Difference diff = new Difference(res);
for(int[] booking : bookings){
int i = booking[0] - 1;
int j = booking[1] - 1;
int val = booking[2];
diff.increment(i, j, val);
}
return diff.result();
}
class Difference{
//差分数组
private int[] diff;
public Difference(int[] nums){
assert nums.length > 0;
//构造差分数组
diff = new int[nums.length];
diff[0] = nums[0];
for(int i = 1; i < nums.length; i++){
diff[i] = nums[i] - nums[i-1];
}
}
//区间增加val
public void increment(int i, int j, int val){
diff[i] += val;
if(j + 1 < diff.length){
diff[j + 1] -= val;
}
}
//构造结果数组
public int[] result(){
int[] res = new int[diff.length];
res[0] = diff[0];
for(int i = 1; i < diff.length; i++){
res[i] = diff[i] + res[i-1];
}
return res;
}
}
}
1.2 队列和栈
单调队列
[239] 滑动窗口最大值

- 题解
class MonotonicQueue {
LinkedList<Integer> q= new LinkedList<Integer>();
public void push(int n){
//小于n的全部删除
while (!q.isEmpty() && q.getLast() < n){
q.pollLast();
}
q.addLast(n);
}
//最大值在头部
public int max(){
return q.getFirst();
}
//已经被删没必要弹出
public void pop(int n){
if(n == q.getFirst()){
q.pollFirst();
}
}
}
class Solution {
int[] maxSlidingWindow(int[] nums, int k){
MonotonicQueue window = new MonotonicQueue();
ArrayList<Integer> arrayList = new ArrayList<>();
for(int i = 0; i < nums.length; i++){
//先填满前k-1个元素在进行滑动
if(i < k - 1){
window.push(nums[i]);
}else{
window.push(nums[i]);
//窗口求最大
arrayList.add(window.max());
window.pop(nums[i-k+1]);
}
}
int[] res = new int[arrayList.size()];
for (int i = 0; i < arrayList.size(); i++) {
res[i] = arrayList.get(i);
}
return res;
}
}
[316] 去除重复字母

- 题解
public class Solution {
public String removeDuplicateLetters(String s) {
//存放去重结果
Stack<Character> stk = new Stack<>();
//记录栈中是否存在某个字符
boolean[] inStack = new boolean[256];
//计数器,记录字符串中字符的数量
int[] count = new int[256];
for (int i = 0; i < s.length(); i++) {
count[s.charAt(i)]++;
}
for (char c : s.toCharArray()) {
//每遍历一次对应计数减一
count[c]--;
//存在栈中跳过
if(inStack[c]) {
continue;
}
//弹出栈顶字典序大的元素
while (!stk.isEmpty() && c < stk.peek()) {
//若字符唯一,停止出栈
if(count[stk.peek()] == 0){
break;
}
//不唯一可以出栈
inStack[stk.pop()] = false;
}
//不存在入栈
stk.push(c);
inStack[c] = true;
}
StringBuilder sb = new StringBuilder();
while (!stk.isEmpty()){
sb.append(stk.pop());
}
//reverse
return sb.reverse().toString();
}
}
1.3 数据结构设计
[380] O(1) 时间插入、删除和获取随机元素

- 题解
public class RandomizedSet {
Map<Integer, Integer> dict;
List<Integer> list;
Random rand = new Random();
public RandomizedSet() {
this.dict = new HashMap();
this.list = new ArrayList();
}
public boolean insert(int val) {
if(dict.containsKey(val)) return false;
dict.put(val,list.size());
list.add(val);
return true;
}
public boolean remove(int val) {
//不存在
if(!dict.containsKey(val)) return false;
//交换最后一个数与val(将val移到列表尾部删除保证时间复杂度为O1)
Integer lastVal = list.get(list.size() - 1);
Integer idx = dict.get(val);
list.set(idx, lastVal);
dict.put(lastVal,idx);
//删除最后一个元素
list.remove(list.size() -1 );
dict.remove(val);
return true;
}
public int getRandom() {
return list.get(rand.nextInt(list.size()));
}
}
[710] 黑名单中的随机数

- 题解
class Solution {
Map<Integer, Integer> map; //黑名单到白名单的映射
Random rand;
int wlen; //白名单的长度
public Solution(int n, int[] blacklist) {
map = new HashMap<>();
rand = new Random();
wlen = n - blacklist.length;
//统计白名单的val
Set<Integer> w = new HashSet<>();
for(int i = wlen; i < n; i++){
w.add(i);
}
//去除白名单中黑名单的val
for(int val : blacklist) w.remove(val);
Iterator<Integer> wi = w.iterator();
//添加映射
for(int val : blacklist){
if(val < wlen){
map.put(val,wi.next());
}
}
}
public int pick() {
int k = rand.nextInt(wlen); //[0,wlen)
return map.getOrDefault(k, k);
}
}
[295] 数据流的中位数

- 题解
class MedianFinder {
//使用两个优先队列,一个大顶堆,一个小顶堆即可
private PriorityQueue<Integer> small;
private PriorityQueue<Integer> large;
public MedianFinder() {
//小顶堆,保存较大的数
large = new PriorityQueue<>();
//大顶堆,保存较小的数
small = new PriorityQueue<>((a, b) ->{return b - a;});
}
//large和small的元素个数之差不超过 1,
//large堆的堆顶元素要大于等于small堆的堆顶元素
public void addNum(int num) {
if(small.size() >= large.size()){
small.offer(num);
large.offer(small.poll());
}else{
large.offer(num);
small.offer(large.poll());
}
}
public double findMedian() {
//元素不一样多,选择多的堆顶元素即为中位数
if(large.size() < small.size()){
return small.peek();
}else if(large.size() > small.size()){
return large.peek();
}
//元素一样多,堆顶元素的均值即为中位数
return (large.peek() + small.peek()) / 2.0;
}
}
2. 二叉树
[226] 翻转二叉树

- 题解
class Solution {
public TreeNode invertTree(TreeNode root) {
//base
if(root == null){
return null;
}
//前序遍历递归交换左右子树
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
invertTree(root.left);
invertTree(root.right);
return root;
}
}
[116] 填充每个节点的下一个右侧节点指针


- 题解
class Solution {
public Node connect(Node root) {
if(root == null) return null;
connectTwoNode(root.left, root.right);
return root;
}
public void connectTwoNode(Node node1, Node node2){
if(node1 == null || node2 == null){
return;
}
node1.next = node2;
//同一节点的左右节点
connectTwoNode(node1.left, node1.right);
connectTwoNode(node2.left, node2.right);
//不同节点的右左
connectTwoNode(node1.right, node2.left);
}
}
[114] 二叉树展开为链表

- 题解
class Solution {
public void flatten(TreeNode root) {
if(root == null) return;
flatten(root.left);
flatten(root.right);
TreeNode left = root.left;
TreeNode right = root.right;
//左子树变为空,右子树接上左子树
root.left = null;
root.right = left;
TreeNode p = root;
while(p.right != null){
p = p.right;
}
//将原先的右子树接到最后
p.right = right;
}
}
[654] 最大二叉树

- 题解
class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
return build(nums, 0, nums.length - 1);
}
TreeNode build(int[] nums,int l, int r){
if(l > r) return null;
//找到数组中的最大值和对应索引
int max = Integer.MIN_VALUE;
int maxi = -1;
//左右边界为l和r
for(int i = l; i <= r; i++){
if(nums[i] > max){
max = nums[i];
maxi = i;
}
}
TreeNode root = new TreeNode(max);
//递归调用左右子树
root.left = build(nums, l, maxi -1);
root.right = build(nums, maxi + 1, r);
return root;
}
}
[105] 从前序与中序遍历序列构造二叉树

- 题解
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
return build(preorder, 0, preorder.length - 1,
inorder, 0, inorder.length -1);
}
TreeNode build(int[] preorder, int preStart, int preEnd,
int[] inorder, int inStart, int inEnd){
if(preStart > preEnd){
return null;
}
//前序遍历的第一个元素为root
int rootVal = preorder[preStart];
//rootVal在中序遍历里的索引
int index = 0;
for(int i = inStart; i < inorder.length; i++){
if(inorder[i] == rootVal){
index = i;
break;
}
}
TreeNode root = new TreeNode(rootVal);
int leftLength = index - inStart;
//递归构造左右子树
root.left = build(preorder, preStart + 1, preStart + leftLength,
inorder, inStart, index - 1);
root.right = build(preorder, preStart + leftLength + 1, preEnd,
inorder, index + 1, inEnd);
return root;
}
}
[106] 从中序与后序遍历序列构造二叉树

- 题解
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
return build(inorder, 0, inorder.length -1 ,
postorder, 0, postorder.length -1);
}
TreeNode build(int[] inorder, int inStart, int inEnd,
int[] postorder, int posStart, int posEnd){
if(inStart > inEnd){
return null;
}
int rootVal = postorder[posEnd];
TreeNode root = new TreeNode(rootVal);
int index = 0;
for(int i = inStart; i <= inEnd; i++){
if(inorder[i] == rootVal){
index = i;
break;
}
}
//左子树长度
int leftLength = index - inStart;
//递归生成左右子树
root.left = build(inorder, inStart, index-1,
postorder, posStart, posStart + leftLength -1);
root.right = build(inorder, index + 1, inEnd,
postorder, posStart + leftLength,posEnd - 1);
return root;
}
}
[652] 寻找重复的子树

- 题解
class Solution {
HashMap<String,Integer> memo = new HashMap<>();
LinkedList<TreeNode> res = new LinkedList<>();
public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
traverse(root);
return res;
}
String traverse(TreeNode root){
if(root == null){
return "#";
}
String left = traverse(root.left);
String right = traverse(root.right);
//记录子树
String subTree = left + "," + right + "," + root.val;
int freq = memo.getOrDefault(subTree, 0);
//多次重复也只会被加入结果集一次
if(freq == 1){
res.add(root);
}
//给对应子树出现的次数加1
memo.put(subTree, freq + 1);
return subTree;
}
}
[297] 二叉树的序列化与反序列化
- 题解- 前序遍历解法
public class Codec {
String SEP = ",";
String NULL = "#";
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
StringBuilder sb = new StringBuilder();
serialize(root, sb);
return sb.toString();
}
void serialize(TreeNode root, StringBuilder sb){
if(root == null) {
sb.append(NULL).append(SEP);
return;
}
//前序遍历位置
sb.append(root.val).append(SEP);
serialize(root.left, sb);
serialize(root.right, sb);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
//将字符串转化为列表
LinkedList<String> nodes = new LinkedList<>();
for(String s : data.split(SEP)){
nodes.addLast(s);
}
return deserialize(nodes);
}
TreeNode deserialize(LinkedList<String> nodes){
if(nodes.isEmpty()) return null;
//列表最左侧就是根节点
String first = nodes.removeFirst();
if(first.equals(NULL)) return null;
TreeNode root = new TreeNode(Integer.parseInt(first));
root.left = deserialize(nodes);
root.right = deserialize(nodes);
return root;
}
}
- 题解- 后序遍历解法
public class Codec {
String SEP = ",";
String NULL = "#";
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
StringBuilder sb = new StringBuilder();
serialize(root, sb);
return sb.toString();
}
void serialize(TreeNode root, StringBuilder sb){
if(root == null) {
sb.append(NULL).append(SEP);
return;
}
serialize(root.left, sb);
serialize(root.right, sb);
//后续遍历位置
sb.append(root.val).append(SEP);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
//将字符串转化为列表
LinkedList<String> nodes = new LinkedList<>();
for(String s : data.split(SEP)) {
nodes.addLast(s);
}
return deserialize(nodes);
}
TreeNode deserialize(LinkedList<String> nodes){
if(nodes.isEmpty()) return null;
//列表最右侧就是根节点
String last = nodes.removeLast();
if(last.equals(NULL)) return null;
TreeNode root = new TreeNode(Integer.parseInt(last));
//先构造右子树再构造左子树
root.right = deserialize(nodes);
root.left = deserialize(nodes);
return root;
}
}
- 题解- 层次遍历解法
public class Codec {
String SEP = ",";
String NULL = "#";
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if(root == null){
return "";
}
StringBuilder sb = new StringBuilder();
//初始化队列,将root加入队列
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while(!q.isEmpty()){
TreeNode cur = q.poll();
//层级遍历
if(cur == null){
sb.append(NULL).append(SEP);
continue;
}
sb.append(cur.val).append(SEP);
q.offer(cur.left);
q.offer(cur.right);
}
return sb.toString();
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
if(data.isEmpty()) return null;
String[] nodes = data.split(SEP);
//第一个元素就是root的值
TreeNode root = new TreeNode(Integer.parseInt(nodes[0]));
//队列q记录父节点,将root加入队列
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
for(int i = 1; i < nodes.length; ){
//队列存父节点
TreeNode parent = q.poll();
//父节点对应的左侧子节点的值
String left = nodes[i++];
if(!left.equals(NULL)){
parent.left = new TreeNode(Integer.parseInt(left));
q.offer(parent.left);
}else{
parent.left = null;
}
//父节点对应的右节点
String right = nodes[i++];
if(!right.equals(NULL)){
parent.right = new TreeNode(Integer.parseInt(right));
q.offer(parent.right);
}else{
parent.right = null;
}
}
return root;
}
}
[1373] 二叉搜索子树的最大键值和

- 题解
1、左右⼦树是否是 BST。
2、左⼦树的最⼤值和右⼦树的最⼩值。
3、左右⼦树的节点值之和。
class Solution {
//全局变量,记录 BST 最⼤节点之和
int maxSum = 0;
public int maxSumBST(TreeNode root){
traverse(root);
return maxSum;
}
public int[] traverse(TreeNode root) {
if(root == null){
return new int[] {
1, Integer.MAX_VALUE,Integer.MIN_VALUE, 0
};
}
//递归计算左右子树
int[] left = traverse(root.left);
int[] right = traverse(root.right);
int[] res = new int[4];
//判断以root为根的二叉树是不是BST
if(left[0] == 1 && right[0] == 1 &&
root.val > left[2] && root.val < right[1]){
//以root为根的二叉树是BST
res[0] = 1;
//计算以 root 为根的这棵 BST 的最⼩值
res[1] = Math.min(left[1], root.val);
// 计算以 root 为根的这棵 BST 的最⼤值
res[2] = Math.max(right[2], root.val);
//计算以 root 为根的这棵 BST 所有节点之和
res[3] = left[3] + right[3] + root.val;
//更新全局变量
maxSum = Math.max(maxSum, res[3]);
}else{
//非BST
res[0] = 0;
}
return res;
}
}
[230] 二叉搜索树中第K小的元素

- 题解
class Solution {
public int kthSmallest(TreeNode root, int k) {
//利用中序遍历特性进行解题
traverse(root, k);
return res;
}
//记录结果
int res = 0;
//记录当前元素的排名
int rank = 0;
void traverse(TreeNode root, int k){
if(root == null){
return;
}
traverse(root.left, k);
rank++;
if(k == rank){
res = root.val;
return;
}
traverse(root.right, k);
}
}
[538] 把二叉搜索树转换为累加树

- 题解
class Solution {
public TreeNode convertBST(TreeNode root) {
traverse(root);
return root;
}
//记录累加和
int sum = 0;
void traverse(TreeNode root){
if(root == null){
return;
}
traverse(root.right);
//维护累加和
sum += root.val;
//将BST转化为累加树
root.val = sum;
traverse(root.left);
}
}
[700] 二叉搜索树中的搜索

- 题解
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
if(root == null){
return null;
}
if(root.val == val){
return root;
}
//左子树
if(root.val > val){
return searchBST(root.left, val);
}
//右子树
if(root.val < val){
return searchBST(root.right, val);
}
return root;
}
}
[701] 二叉搜索树中的插入操作

class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
// 找到空位置插⼊新节点
if(root == null){
return new TreeNode(val);
}
if(val < root.val){
root.left = insertIntoBST(root.left, val);
}
if(val > root.val){
root.right = insertIntoBST(root.right, val);
}
return root;
}
}
[450] 删除二叉搜索树中的节点

- 题解
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if(root == null){
return null;
}
if(root.val == key){
//这两个 if 把情况 1 和 2 都正确处理了(有一个节点或者没有节点)
if(root.left == null) return root.right;
if(root.right == null) return root.left;
//情况3(该节点有两个子节点)
TreeNode minNode = getMin(root.right);
root.val = minNode.val;
root.right = deleteNode(root.right, minNode.val);
} else if(root.val > key){
root.left = deleteNode(root.left, key);
} else if(root.val < key){
root.right = deleteNode(root.right, key);
}
return root;
}
TreeNode getMin(TreeNode node){
while(node.left != null){
node =node.left;
}
return node;
}
}
[98] 验证二叉搜索树
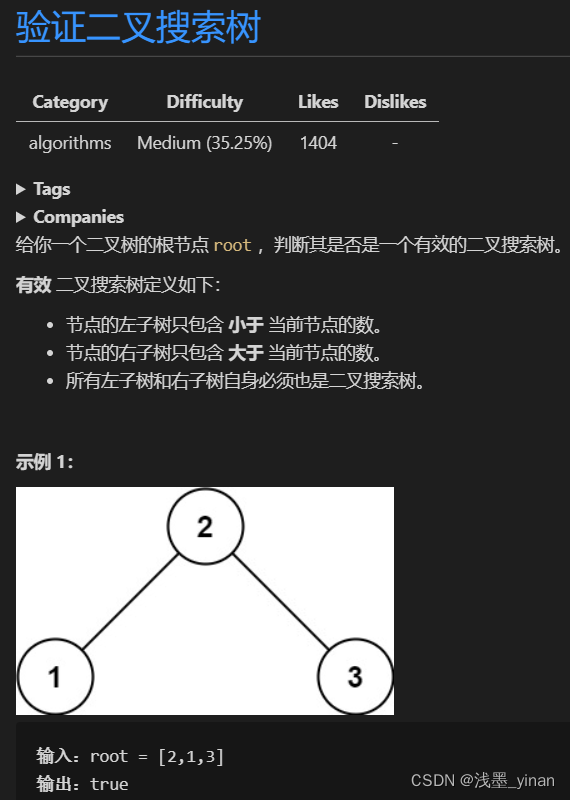
- 题解
满足条件:限定以 root 为根的⼦树节点必须满⾜ max.val > root.val > min.val
class Solution {
public boolean isValidBST(TreeNode root) {
return isValidBST(root, null, null);
}
boolean isValidBST(TreeNode root, TreeNode minNode, TreeNode maxNode){
if(root == null){
return true;
}
if(minNode != null && root.val <= minNode.val){
return false;
}
if(maxNode != null && root.val >= maxNode.val){
return false;
}
return isValidBST(root.left, minNode, root) &&
isValidBST(root.right, root, maxNode);
}
}
[96] 不同的二叉搜索树

- 题解
class Solution {
// 备忘录
int[][] memo;
int numTrees(int n) {
// 备忘录的值初始化为 0
memo = new int[n + 1][n + 1];
return count(1, n);
}
int count(int lo, int hi) {
if (lo > hi) return 1;
// 查备忘录
if (memo[lo][hi] != 0) {
return memo[lo][hi];
}
int res = 0;
for (int mid = lo; mid <= hi; mid++) {
int left = count(lo, mid - 1);
int right = count(mid + 1, hi);
res += left * right;
}
// 将结果存入备忘录
memo[lo][hi] = res;
return res;
}
}
[95] 不同的二叉搜索树 II

- 题解
class Solution {
public List<TreeNode> generateTrees(int n) {
if(n == 0){
return new LinkedList<>();
}
return build(1, n);
}
List<TreeNode> build(int lo, int hi){
List<TreeNode> res = new LinkedList<>();
if(lo > hi){
res.add(null);
return res;
}
//1、穷举 root 节点的所有可能。
for(int i = lo; i <= hi; i++){
// 2、递归构造出左右子树的所有合法 BST。
List<TreeNode> left = build(lo, i -1);
List<TreeNode> right = build(i + 1, hi);
// 3、给 root 节点穷举所有左右子树的组合。
for(TreeNode l : left){
for(TreeNode r : right){
// i 作为根节点 root 的值
TreeNode root = new TreeNode(i);
root.left = l;
root.right = r;
res.add(root);
}
}
}
return res;
}
}
3. 动态规划
思路:当前问题的解加上子问题的最优解,使用状态转移进行更新子问题的解。可以使用递归分解子问题(可以用备忘录去除重叠子问题)或者进行状态转移由base解往前推。
[509] 斐波那契数

- 代码
使用备忘录消除重叠子问题
class Solution {
public int fib(int n) {
//备忘录初始化为0
int[] memo = new int[n + 1];
//使用带备忘录的递归
return helper(memo, n);
}
int helper(int[] memo, int n){
//basecase
if(n == 0 || n == 1){
return n;
}
//已经计算过
if(memo[n] != 0){
return memo[n];
}
memo[n] = helper(memo, n-1) + helper(memo, n-2);
return memo[n];
}
}
[322] 零钱兑换
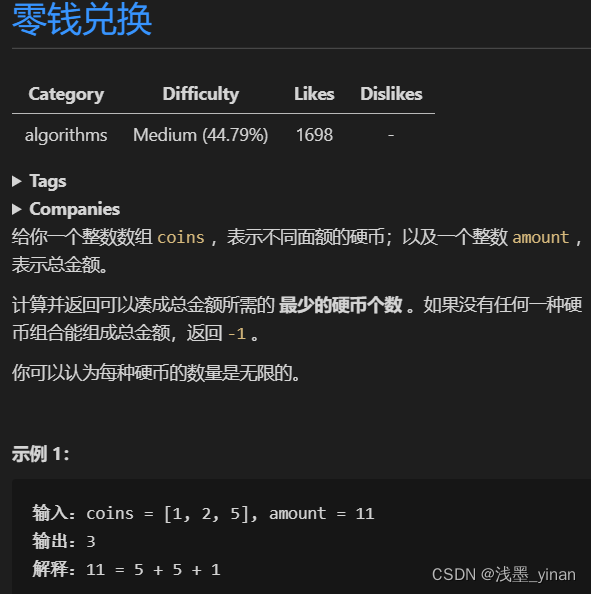
- 题解
dp 数组的定义:当⽬标⾦额为 i 时,⾄少需要 dp[i] 枚硬币凑出
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
//数组⼤⼩为 amount + 1,初始值也为 amount + 1
Arrays.fill(dp, amount + 1);
//base case
dp[0] = 0;
//外层for循环在遍历所有状态的所有取值
for(int i = 0; i < dp.length; i++){
// 内层 for 循环在求所有选择的最⼩值
for(int coin : coins){
// ⼦问题⽆解,跳过
if(i - coin < 0){
continue;
}
dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
}
}
return (dp[amount] == amount + 1) ? -1 : dp[amount];
}
}
[931] 下降路径最小和

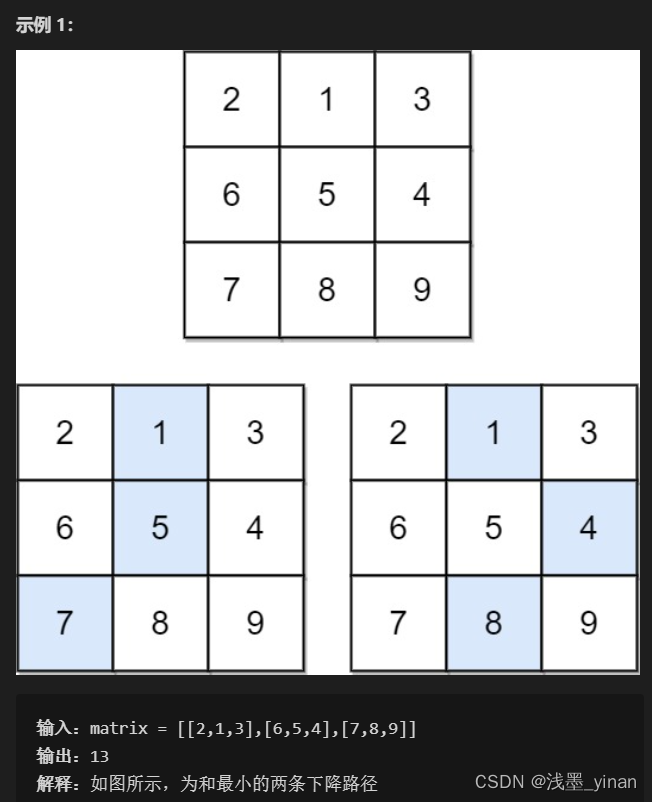
- 代码
class Solution {
public int minFallingPathSum(int[][] matrix) {
int n = matrix.length;
int res = Integer.MAX_VALUE;
//备忘录初始化为66666
memo = new int[n][n];
for(int i = 0; i < n; i++){
Arrays.fill(memo[i], 66666);
}
//终点可能在 matrix[n-1] 的任意⼀列
for(int j = 0; j < n; j++){
res = Math.min(res, dp(matrix, n - 1, j ));
}
return res;
}
//备忘录
int[][] memo;
int dp(int[][] matrix, int i, int j){
// 1、索引合法性检查
if(i < 0 || j < 0 ||
i >= matrix.length ||
j >= matrix.length){
return 99999;
}
//2. base case
if(i == 0){
return matrix[0][j];
}
//3.查找备忘录,防止重复计算
if(memo[i][j] != 66666){
return memo[i][j];
}
//进行状态转移
memo[i][j] = matrix[i][j] + min(
dp(matrix, i - 1 , j),
dp(matrix, i - 1, j - 1),
dp(matrix, i - 1, j + 1)
);
return memo[i][j];
}
int min(int a, int b ,int c) {
return Math.min(a, Math.min(b, c));
}
}
[300] 最长递增子序列

- 题解
dp[i] 表示以 nums[i] 这个数结尾的最⻓递增⼦序列的⻓度。
class Solution {
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
//初始化为1
Arrays.fill(dp, 1);
//状态转移
for(int i = 0; i < nums.length; i++){
for(int j = 0; j < i; j++){
if(nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
int res = 0;
for(int i = 0; i < nums.length; i++){
res = Math.max(res, dp[i]);
}
return res;
}
}
[53] 最大子数组和

- 题解
nums[i] 为结尾的「最⼤⼦数组和」为 dp[i]。
这种定义之下,想得到整个 nums 数组的「最⼤⼦数组和」,不能直接返回 dp[n-1],⽽需要遍历整个 dp数组
class Solution {
public int maxSubArray(int[] nums) {
int n = nums.length;
if(n == 0) return 0;
int[] dp = new int[n];
//basecase
// 第⼀个元素前⾯没有⼦数组
dp[0] = nums[0];
//状态转移
for(int i = 1; i < n; i++){
// 要么⾃成⼀派,要么和前⾯的⼦数组合并
dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
}
//求最大数组
int res = Integer.MIN_VALUE;
for(int i = 0; i < n; i++){
res = Math.max(res, dp[i]);
}
return res;
}
}
[1143] 最长公共子序列

- 题解
这个dp函数的定义是:dp(s1, i, s2, j)计算s1[i…]和s2[j…]的最长公共子序列长度。
class Solution {
// 备忘录,消除重叠子问题
int[][] memo;
public int longestCommonSubsequence(String text1, String text2) {
int m = text1.length(), n = text2.length();
// 备忘录值为 -1 代表未曾计算
memo = new int[m][n];
for(int[] row : memo){
Arrays.fill(row, -1);
}
return dp(text1, 0, text2, 0);
}
// 定义:计算最长公共子序列长度
int dp(String s1,int i ,String s2, int j){
//basecase
if(i == s1.length() || j == s2.length()){
return 0;
}
// 如果之前计算过,则直接返回备忘录中的答案
if(memo[i][j] != -1){
return memo[i][j];
}
// 根据 s1[i] 和 s2[j] 的情况做选择
if(s1.charAt(i)==s2.charAt(j)){
//s1[i] 和 s2[j] 必然在 lcs 中
memo[i][j] = 1 + dp(s1, i + 1, s2, j + 1);
} else {
// s1[i] 和 s2[j] 至少有一个不在 lcs 中
memo[i][j] = Math.max(
dp(s1, i + 1, s2, j),
dp(s1, i, s2, j + 1)
);
}
return memo[i][j];
}
}
[583] 两个字符串的删除操作

- 题解
求出两字符串的LCS,在减去源字符串即可
class Solution {
public int minDistance(String word1, String word2) {
int lcs = longestCommonSubsequence(word1, word2);
return word1.length() - lcs + word2.length() - lcs;
}
// 备忘录,消除重叠子问题
int[][] memo;
public int longestCommonSubsequence(String text1, String text2) {
int m = text1.length(), n = text2.length();
// 备忘录值为 -1 代表未曾计算
memo = new int[m][n];
for(int[] row : memo){
Arrays.fill(row, -1);
}
return dp(text1, 0, text2, 0);
}
// 定义:计算最长公共子序列长度
int dp(String s1,int i ,String s2, int j){
//basecase
if(i == s1.length() || j == s2.length()){
return 0;
}
// 如果之前计算过,则直接返回备忘录中的答案
if(memo[i][j] != -1){
return memo[i][j];
}
// 根据 s1[i] 和 s2[j] 的情况做选择
if(s1.charAt(i)==s2.charAt(j)){
//s1[i] 和 s2[j] 必然在 lcs 中
memo[i][j] = 1 + dp(s1, i + 1, s2, j + 1);
} else {
// s1[i] 和 s2[j] 至少有一个不在 lcs 中
memo[i][j] = Math.max(
dp(s1, i + 1, s2, j),
dp(s1, i, s2, j + 1)
);
}
return memo[i][j];
}
}
[712] 两个字符串的最小ASCII删除和

- 题解
class Solution {
//备忘录
int memo[][];
public int minimumDeleteSum(String s1, String s2) {
int m = s1.length(), n = s2.length();
// 备忘录值为 -1 代表未曾计算
memo = new int[m][n];
for(int[] row : memo){
Arrays.fill(row, -1);
}
return dp(s1, 0, s2, 0);
}
// 定义:将 s1[i..] 和 s2[j..] 删除成相同字符串,
// 最小的 ASCII 码之和为 dp(s1, i, s2, j)。
int dp(String s1, int i, String s2, int j){
int res = 0;
//base case
if(i == s1.length()){
// 如果 s1 到头了,那么 s2 剩下的都得删除
for(; j < s2.length(); j++){
res += s2.charAt(j);
}
return res;
}
if(j == s2.length()){
// 如果 s2 到头了,那么 s1 剩下的都得删除
for(; i < s1.length(); i++){
res += s1.charAt(i);
}
return res;
}
if(memo[i][j] != -1){
return memo[i][j];
}
if(s1.charAt(i) == s2.charAt(j)){
// s1[i] 和 s2[j] 都是在 lcs 中的,不用删除
memo[i][j] = dp(s1, i + 1, s2, j + 1);
} else {
// s1[i] 和 s2[j] 至少有一个不在 lcs 中,删一个
memo[i][j] = Math.min(
s1.charAt(i) + dp(s1,i + 1, s2, j),
s2.charAt(j) + dp(s1, i, s2, j + 1)
);
}
return memo[i][j];
}
}
[72] 编辑距离

- 题解
定义:dp(i, j) 返回 s1[0…i] 和 s2[0…j] 的最⼩编辑距离
class Solution {
public int minDistance(String word1, String word2) {
int m = word1.length(), n = word2.length();
int[][] dp = new int[m+1][n+1];
//base case
for(int i = 1; i <= m; i++)
dp[i][0] = i;
for(int j = 1; j <= n; j++)
dp[0][j] = j;
//自底向上
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(word1.charAt(i - 1) == word2.charAt(j - 1))
dp[i][j] = dp[i - 1][j - 1];
else
dp[i][j] = min(
dp[i - 1][j] + 1,
dp[i][j - 1] + 1,
dp[i - 1][j - 1] + 1
);
}
}
return dp[m][n];
}
int min(int a, int b, int c){
return Math.min(a, Math.min(b, c));
}
}
[10] 正则表达式匹配

- 题解
正则表达算法问题只需要把住⼀个基本点:看两个字符是否匹配,⼀切逻辑围绕匹配/不匹配两种情况展开即可 。
dp函数的定义如下:
若dp(s,i,p,j) = true,则表示s[i…]可以匹配p[j…];若dp(s,i,p,j) = false,则表示s[i…]无法匹配p[j…]。
class Solution {
public boolean isMatch(String s, String p) {
// 指针 i,j 从索引 0 开始移动
return dp(s, 0, p, 0);
}
// 备忘录
HashMap<String, Boolean> memo = new HashMap<>();
boolean dp(String s, int i, String p, int j){
int m = s.length(), n = p.length();
//base case
//模式串p已经被匹配完了
if(j == n){
//s也恰好被匹配完,则说明匹配成功
return i == m;
}
//文本串s已经全部被匹配了
if(i == m){
// 如果能匹配空串,一定是字符和 * 成对儿出现
if((n - j) % 2 == 1){
return false;
}
// 检查是否为 x*y*z* 这种形式
for(; j + 1 < n; j += 2){
if(p.charAt(j + 1)!= '*'){
return false;
}
}
return true;
}
// 记录状态 (i, j),消除重叠子问题
String key = String.valueOf(i) + "," + String.valueOf(j);
if(memo.containsKey(key)) return memo.get(key);
boolean res = false;
// 匹配
if(s.charAt(i) == p.charAt(j) || p.charAt(j) == '.'){
if(j < n - 1 && p.charAt(j + 1) == '*'){
// 1.1 通配符匹配 0 次或多次
res = dp(s, i, p, j + 2) || dp(s, i + 1,p, j);
}else{
// 1.2 常规匹配 1 次
res = dp(s,i + 1, p, j + 1);
}
} else {
// 不匹配
// 2.1 通配符匹配 0 次
if (j < n - 1 && p.charAt(j + 1) == '*') {
res = dp(s, i, p, j + 2);
} else {
// 2.2 无法继续匹配
res = false;
}
}
//将当前记录结果计入备忘录
memo.put(key, res);
return res;
}
}
0-1背包问题
给你⼀个可装载重量为 W 的背包和 N 个物品,每个物品有重量和价值两个属性。其中第 i 个物品的重量为wt[i],价值为 val[i],现在让你⽤这个背包装物品,最多能装的价值是多少?
举个简单的例⼦,输⼊如下:
N = 3, W = 4
wt = [2, 1, 3]
val = [4, 2, 3]
算法返回 6,选择前两件物品装进背包,总重量 3 ⼩于 W,可以获得最⼤价值 6.
- 题解
dp[i][w] 的定义如下:对于前 i 个物品,当前背包的容量为 w,这种情况下可以装的最⼤价值是 dp[i][w]。
⽐如说,如果 dp[3][5] = 6,其含义为:对于给定的⼀系列物品中,若只对前 3 个物品进⾏选择,当背包
容量为 5 时,最多可以装下的价值为 6。
public class Solution {
int knapsack(int W, int N, int[] wt, int[] val) {
//base case
int[][] dp = new int[N + 1][W + 1];
for (int i = 1; i <= N; i++) {
for (int w = 1; w <= W; w++) {
if (w - wt[i - 1] < 0) {
// 这种情况下只能选择不装⼊背包
//最⼤价值 dp[i][w] 应该等于 dp[i-1][w],继承之前
//的结果
dp[i][w] = dp[i - 1][w];
} else {
// 装⼊或者不装⼊背包,择优
//如果装了第 i 个物品,就要寻求剩余重量 w - wt[i-1] 限制
//下的最⼤价值,加上第 i 个物品的价值 val[i-1]。
//i 是从 1 开始的,所以 val 和 wt 的索引是 i-1 时表示第 i 个物品的价值和重量。
dp[i][w] = Math.max(val[i - 1] + dp[i - 1][w - wt[i - 1]],
dp[i - 1][w]);
}
}
}
return dp[N][W];
}
public static void main(String[] args) {
int[] wt = new int[]{2, 1, 3};
int[] val = new int[]{4, 2, 3};
Solution solution = new Solution();
int knapsack = solution.knapsack(4, 3, wt, val);
System.out.println(knapsack);
}
}
[416] 分割等和子集

- 题解
问题转换为背包问题:
dp[N][sum/2],base case 就是 dp[…][0] = true 和 dp[0][…] = false,因为背包没有空间的时候,就相当于装满了,⽽当没有物品可选择的时候,肯定没办法装满背包
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0;
for(int num : nums){
sum += num;
}
// 和为奇数时,不可能划分成两个和相等的集合
if(sum % 2 != 0){
return false;
}
int n = nums.length;
sum = sum / 2;
boolean[][] dp = new boolean[n + 1][sum + 1];
//base case
for(int i = 0; i <= n; i++){
dp[i][0] = true;
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= sum; j++){
if(j - nums[i - 1] < 0){
dp[i][j] = dp[i -1][j];
} else {
//装入或不装入背包
//注意这里装入该物品时,数量减一,为dp[i-1][j-nums[i-1]]
//区分完全背包问题。硬币数量是无限的
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];
}
}
}
return dp[n][sum];
}
}
[518] 零钱兑换 II

- 题解
class Solution {
public int change(int amount, int[] coins) {
int n = coins.length;
int[][] dp = new int[n + 1][amount + 1];
for(int i = 0; i <= n; i++){
dp[i][0] = 1;
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= amount; j++){
if(j - coins[i - 1] < 0){
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i - 1]]; //注意硬币数量是无线的,将第i枚硬币装入后,数量不会少,所以是dp[i][j - coins[i - 1]]
}
}
}
return dp[n][amount];
}
}
[121] 买卖股票的最佳时机

- 题解
dp[i][k][0 or 1]- 0 <= i <= n - 1, 1 <= k <= K
- n 为天数,⼤ K 为交易数的上限,0 和 1 代表是否持有股票。
- 此问题共 n × K × 2 种状态,全部穷举就能搞定。
- k = 1,交易次数为1
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int[][] dp = new int[n][2];
for(int i = 0; i < n; i++){
if(i - 1 == -1){
//base case
dp[i][0] = 0;
dp[i][1] = -prices[i];
continue;
}
dp[i][0] =Math.max( dp[i - 1][0], dp[i-1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], - prices[i]);
}
return dp[n - 1][0];
}
}
[122] 买卖股票的最佳时机 II

- 题解
k = + infinity
如果 k 为正⽆穷,那么就可以认为 k 和 k - 1 是⼀样的。可以这样改写框架
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int[][] dp = new int[n][2];
for(int i = 0; i < n; i++){
if(i - 1 == -1){
dp[i][0] = 0;
dp[i][1] = -prices[i];
continue;
}
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
}
}
[123] 买卖股票的最佳时机 III

- 题解
k = 2
class Solution {
int maxProfit(int[] prices) {
int max_k = 2, n = prices.length;
int[][][] dp = new int[n][max_k + 1][2];
for (int i = 0; i < n; i++) {
for (int k = 1; k <= max_k; k++) {
if (i - 1 == -1) {
// 处理 base case
dp[i][k][0] = 0;
dp[i][k][1] = -prices[i];
continue;
}
dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] +
prices[i]);
dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] -
prices[i]);
}
}
// 穷举了 n × max_k × 2 个状态,正确。
return dp[n - 1][max_k][0];
}
}
[188] 买卖股票的最佳时机 IV

- 题解
将K=Infinity,与k=2两种情况结合即可。
class Solution {
public int maxProfit(int k, int[] prices) {
int n = prices.length;
if(n <= 0){
return 0;
}
if(k > n/2){
// 交易次数 k 没有限制的情况
return maxProfit_infit(prices);
}
int [][][] dp = new int[n][k+1][2];
for(int i = 0; i < n; i++){
for(int j = 1; j <= k;j++){
if(i - 1 == -1){
dp[i][j][0] = 0;
dp[i][j][1] = -prices[i];
continue;
}
dp[i][j][0] = Math.max(dp[i-1][j][0], dp[i - 1][j][1] + prices[i]);
dp[i][j][1] = Math.max(dp[i-1][j][1], dp[i - 1][j - 1][0] - prices[i]);
}
}
return dp[n - 1][k][0];
}
public int maxProfit_infit(int[] prices) {
int n = prices.length;
int[][] dp = new int[n][2];
for(int i = 0; i < n; i++){
if(i - 1 == -1){
dp[i][0] = 0;
dp[i][1] = -prices[i];
continue;
}
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
}
}
[309] 最佳买卖股票时机含冷冻期

- 题解
k = +infinity with cooldown
每次 sell 之后要等⼀天才能继续交易
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int[][] dp = new int[n][2];
for(int i = 0; i < n; i++){
if(i - 1 == -1){
dp[i][0] = 0;
dp[i][1] = -prices[i];
continue;
}
if(i - 2 == -1){
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i-1][1], - prices[i]);
continue;
}
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 2][0] - prices[i]);
}
return dp[n -1][0];
}
}
[714] 买卖股票的最佳时机含手续费

- 题解
k = +infinity with fee
每次交易要⽀付⼿续费,只要把⼿续费从利润中减去即可。相当于买⼊股票的价格升⾼了
class Solution {
public int maxProfit(int[] prices, int fee) {
int n = prices.length;
int[][] dp = new int[n][2];
for(int i = 0; i < n; i++){
if( i - 1 == -1){
dp[i][0] = 0;
dp[i][1] = -prices[i] - fee;
continue;
}
dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
dp[i][1] = Math.max(dp[i -1][1], dp[i - 1][0] - prices[i] - fee);
}
return dp[n-1][0];
}
}
[198] 打家劫舍

- 题解
- 你面前房子的索引就是状态,抢和不抢就是选择.
- 如果你抢了这间房子,那么你肯定不能抢相邻的下一间房子了,只能从下下间房子开始做选择。
- 如果你不抢这间房子,那么你可以走到下一间房子前,继续做选择。
class Solution {
public int rob(int[] nums) {
int n = nums.length;
// dp[i] = x 表示:
// 从第 i 间房子开始抢劫,最多能抢到的钱为 x
// base case: dp[n] = 0,注意倒着退
int[] dp = new int[n + 2];
for(int i = n-1; i >= 0; i--){
dp[i] = Math.max(dp[i + 1],nums[i] + dp[i + 2]);
}
return dp[0];
}
}
[213] 打家劫舍 II

- 题解
首先,首尾房间不能同时被抢,那么只可能有三种不同情况:要么都不被抢(略);要么第一间房子被抢最后一间不抢;要么最后一间房子被抢第一间不抢。
class Solution {
public int rob(int[] nums) {
int n = nums.length;
if (n == 1) return nums[0];
return Math.max(robRange(nums, 0, n - 2),
robRange(nums, 1, n - 1));
}
int robRange(int[] nums, int start, int end){
int n = nums.length;
int[] dp = new int[n + 2];
for(int i = end; i >= start; i--){
dp[i] = Math.max(dp[i+1], nums[i]+dp[i+2]);
}
return dp[start];
}
}
[337] 打家劫舍 III

- 题解
class Solution {
Map<TreeNode,Integer> memo = new HashMap<>();
public int rob(TreeNode root) {
if(root == null){
return 0;
}
// 利用备忘录消除重叠子问题
if(memo.containsKey(root)){
return memo.get(root);
}
// 抢,然后去下下家
int do_it = root.val + (root.left == null ? 0 : rob(root.left.left) + rob(root.left.right)) +
(root.right == null ? 0 : rob(root.right.left) + rob(root.right.right));
// 不抢,然后去下家
int not_do = rob(root.left) + rob(root.right);
int res = Math.max(do_it, not_do);
memo.put(root, res);
return res;
}
}
[64] 最小路径和

- 题解
class Solution {
int[][] memo;
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
// 构造备忘录,初始值全部设为 -1
memo = new int[m][n];
for(int[] row : memo){
Arrays.fill(row, -1);
}
// 计算从左上⻆⾛到右下⻆的最⼩路径和
return dp(grid, m-1, n-1);
}
int dp(int[][] grid, int m, int n){
if(m == 0 && n == 0){
return grid[0][0];
}
// 如果索引出界,返回⼀个很⼤的值,
// 保证在取 min 的时候不会被取到
if(m < 0 || n < 0){
return Integer.MAX_VALUE;
}
//避免重复计算
if(memo[m][n] != -1){
return memo[m][n];
}
// 将计算结果记⼊备忘录
// 左边和上⾯的最⼩路径和加上 grid[i][j]
// 就是到达 (i, j) 的最⼩路径和
memo[m][n] = Math.min(dp(grid, m-1, n),
dp(grid, m,n - 1))+ grid[m][n];
return memo[m][n];
}
}
[887] 鸡蛋掉落

- 题解
递归没碎,碎了两种状态
class Solution {
HashMap<String, Integer> memo = new HashMap<>();
public int superEggDrop(int k, int n) {
return dp(k, n);
}
int dp(int k, int n){
//base case
if(k == 1) return n;
if(n == 0) return 0;
//避免重复计算
String key = k+"#"+n;
if(memo.containsKey(key)) return memo.get(key);
int res = Integer.MAX_VALUE;
//穷举所有可能的选择
// for(int i = 1 ; i <= n; i++){
// res = Math.min(res, Math.max(dp(k, n-i), dp(k-1, i-1))+1); //没碎,碎了
// }
//使用二分搜索
int lo = 1, hi = n;
while(lo <= hi){
int mid = (lo + hi) / 2;
int broken = dp(k - 1, mid - 1);
int not_broken = dp(k, n - mid);
if(broken > not_broken){
hi = mid - 1;
res = Math.min(res, broken + 1);
} else {
lo = mid + 1;
res = Math.min(res, not_broken + 1);
}
}
//记入备忘录
memo.put(key,res);
return res;
}
}
回文串
[5] 最长回文子串

- 题解
class Solution {
public String longestPalindrome(String s) {
String str = "";
for(int i = 0; i < s.length(); i++){
// 找到以 s[i] 为中心的回文串
String str1 = Palindrome(s,i,i);
//找到以 s[i] 和 s[i+1] 为中心的回文串
String str2 = Palindrome(s,i,i+1);
str = str1.length()>str.length()?str1:str;
str = str2.length()>str.length()?str2:str;
}
return str;
}
String Palindrome(String s,int l ,int r){
while(l>=0&&r<s.length()&&s.charAt(l)==s.charAt(r)){
//向两边扩散
l--;r++;
}
//获取子字符串
return s.substring(l+1,r);
}
}
[1312] 让字符串成为回文串的最少插入次数

- 题解
dp数组定义:对 s[i…j],最少需要插入 dp[i][j] 次才能变成回文。
class Solution {
public int minInsertions(String s) {
int n = s.length();
// 定义:对 s[i..j],最少需要插入 dp[i][j] 次才能变成回文
int[][] dp = new int[n][n];
// base case:i == j 时 dp[i][j] = 0,单个字符本身就是回文
// dp 数组已经全部初始化为 0,base case 已初始化
// 从下向上遍历
for(int i = n - 2; i >= 0; i--){
//从左往右遍历
for(int j = i + 1; j < n; j++){
if(s.charAt(i) == s.charAt(j)){
dp[i][j] = dp[i + 1][j - 1];
} else {
dp[i][j] = Math.min(dp[i + 1][j], dp[i][j - 1]) + 1;
}
}
}
// 根据 dp 数组的定义,题目要求的答案
return dp[0][n-1];
}
}
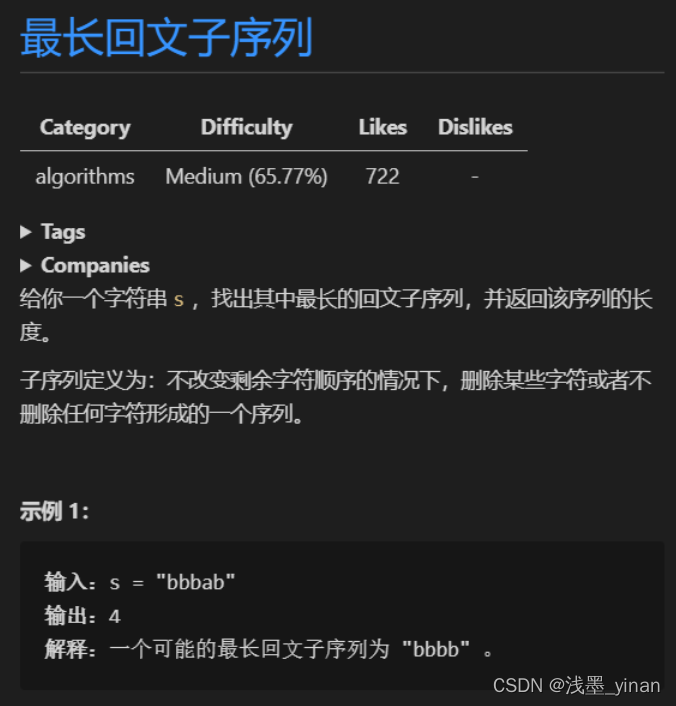
[516] 最长回文子序列
- 题解
在子串s[i…j]中,最长回文子序列的长度为dp[i][j]
class Solution {
public int longestPalindromeSubseq(String s) {
int n = s.length();
//初始化dp数组
int[][] dp = new int[n][n];
//base case
for(int i = 0; i < n; i++){
dp[i][i] = 1;
}
//反着遍历保证正确的状态转移
for(int i = n - 1;i >= 0; i--){
for(int j = i + 1; j < n; j++){
//状态转移
if(s.charAt(i) == s.charAt(j)){
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j -1]);
}
}
}
// 整个 s 的最长回文子串长度
return dp[0][n - 1];
}
}
651. 四键键盘

- 题解
dp[i]表示i次操作后最多能显示多少个A,要使A最多最后一次操作要么为A,要么为C-V
class Solution {
int maxA(int N){
int[] dp = new int[N + 1];
dp[0] = 0;
for(int i = 1; i <= N; i++){
//这次按A
dp[i] = dp[i - 1] + 1;
//这次按C-V,穷举按C-A,C-V的时机
for(int j = 2; j < i; j++){
//全选并复制dp[j - 2],连续粘贴i- j次
//屏幕上共dp[j -2] * (i - j + 1)个A
dp[i] = Math.max(dp[i], dp[j - 2] * (i - j + 1));
}
}
return dp[N];
}
}
[312] 戳气球

-
题解
- dp[i][j] = x表示,戳破气球i和气球j之间(开区间,不包括i和j)的所有气球,可以获得的最高分数为x。
- 其实气球i和气球j之间的所有气球都可能是最后被戳破的那一个,不防假设为k。i和j就是两个「状态」,最后戳破的那个气球k就是「选择」。
- 如果最后一个戳破气球k,dp[i][j]的值应该为:
dp[i][j] = dp[i][k] + dp[k][j] + points[i]*points[k]*points[j]
class Solution {
public int maxCoins(int[] nums) {
int n = nums.length;
// 添加两侧的虚拟气球
int[] points = new int[n + 2];
points[0] = points[n + 1] = 1;
for(int i = 1; i <= n; i++){
points[i] = nums[i - 1];
}
// base case 已经都被初始化为 0
int[][] dp = new int[n + 2][n + 2];
// 开始状态转移
// i 应该从下往上
for(int i = n; i >= 0; i--){
// j 应该从左往右
for(int j = i + 1; j < n + 2; j++){
// 最后戳破的气球是哪个?
for(int k = i + 1;k < j; k++){
// 择优做选择
dp[i][j] = Math.max(
dp[i][j],
dp[i][k] + dp[k][j] + points[i] * points[j] * points[k]
);
}
}
}
return dp[0][n + 1];
}
}
3.1 贪心算法
什么是贪心算法呢?贪心算法可以认为是动态规划算法的一个特例,相比动态规划,使用贪心算法需要满足更多的条件(贪心选择性质),但是效率比动态规划要高。
[435] 无重叠区间

- 题解
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
if(intervals.length == 0) return 0;
Arrays.sort(intervals,(o1,o2)->{
if(o1[1]>o2[1]) return 1;
if(o1[1]<o2[1]) return -1;
return 0;});
//至少有一个区间不相交
int count = 1;
int end = intervals[0][1];
for(int[] interval : intervals){
int start = interval[0];
if(start >= end){
// 找到下一个选择的区间了
count++;
end = interval[1];
}
}
return intervals.length - count;
}
}
[452] 用最少数量的箭引爆气球

- 题解
等号相等算重叠
class Solution {
public int findMinArrowShots(int[][] points) {
if(points.length == 0) return 0;
Arrays.sort(points,(o1,o2)->{
if(o1[1]>o2[1]) return 1;
if(o1[1]<o2[1]) return -1;
return 0;});
//至少有一个区间不相交
int count = 1;
int end = points[0][1];
for(int[] interval : points){
int start = interval[0];
if(start > end){
// 找到下一个选择的区间了
count++;
end = interval[1];
}
}
return count;
}
}
[55] 跳跃游戏

- 题解
class Solution {
public boolean canJump(int[] nums) {
int n = nums.length;
int farthest = 0;
for(int i = 0; i < n - 1; i++){
//nums[i] = 0,若
farthest = Math.max(farthest, i + nums[i]);
if(farthest == i){
return false;
}
}
return farthest >= n - 1;
}
}
[45] 跳跃游戏 II

- 题解
i 和 end 标记了可以选择的跳跃步数,farthest 标记了所有选择 [i…end] 中能够跳到的最远距离,jumps 记录了跳跃次数
class Solution {
public int jump(int[] nums) {
int n = nums.length;
//最远能跳到索引end
int end = 0;
//最远能跳的距离
int farthest = 0;
int jump = 0;
for(int i = 0; i < n - 1; i++){
farthest = Math.max(nums[i] + i, farthest);
if (end == i) {
jump++;
end = farthest;
}
}
return jump;
}
}
[253] 会议室 II(中等)

- 题解
int minMeetingRooms(int[][] meetings) {
int n = meetings.length;
int[] begin = new int[n];
int[] end = new int[n];
for(int i = 0; i < n; i++) {
begin[i] = meetings[i][0];
end[i] = meetings[i][1];
}
Arrays.sort(begin);
Arrays.sort(end);
// 扫描过程中的计数器
int count = 0;
// 双指针技巧
int res = 0, i = 0, j = 0;
while (i < n && j < n) {
if (begin[i] < end[j]) {
// 扫描到一个红点
count++;
i++;
} else {
// 扫描到一个绿点
count--;
j++;
}
// 记录扫描过程中的最大值
res = Math.max(res, count);
}
return res;
}
[1024] 视频拼接

- 题解
class Solution {
public int videoStitching(int[][] clips, int T) {
if (T == 0) return 0;
// 按起点升序排列,起点相同的降序排列
Arrays.sort(clips, (a, b) -> {
if (a[0] == b[0]) {
return b[1] - a[1];
}
return a[0] - b[0];
});
// 记录选择的短视频个数
int res = 0;
// 当前段的结尾数字,默认为0 因为要用若干短视频凑出完成视频[0, T],至少得有一个短视频的起点是 0
int curEnd = 0, nextEnd = 0;// 下一个时段的结尾数字
int i = 0, n = clips.length;
while (i < n && clips[i][0] <= curEnd) {
// 在第 res 个视频的区间内贪心选择下一个视频
while (i < n && clips[i][0] <= curEnd) {
nextEnd = Math.max(nextEnd, clips[i][1]);
i++;
}
// 找到下一个视频,更新 curEnd
res++;
curEnd = nextEnd;
if (curEnd >= T) {
// 已经可以拼出区间 [0, T]
return res;
}
}
// 无法连续拼出区间 [0, T]
return -1;
}
}
[1288] 删除被覆盖区间

- 题解
class Solution {
public int removeCoveredIntervals(int[][] intervals) {
// 按照起点升序排列,起点相同时降序排列
Arrays.sort(intervals, (o1, o2)->{
if(o1[0] == o2[0]) return o2[1] - o1[1];
return o1[0] - o2[0];
});
//记录合并区间的起点和终点
int left = intervals[0][0];
int right = intervals[0][1];
int res = 0;
for(int i = 1; i < intervals.length; i++){
int[] interval = intervals[i];
//情况一,找到覆盖区间
if(left <= interval[0] && right >= interval[1]){
res++;
}
//情况二,找到相交区间,合并
if(right >= interval[0] && right <= interval[1]){
right = interval[1];
}
//情况三,完全不相交,更新起点和终点
if(right < interval[0]){
left = interval[0];
right =interval[1];
}
}
return intervals.length - res;
}
}
[56] 合并区间

- 题解

class Solution {
public int[][] merge(int[][] intervals) {
if(intervals.length == 0) return null;
//按区间的升序排序
Arrays.sort(intervals, (o1, o2)-> o1[0] - o2[0]);
int[][] res = new int[intervals.length][2];
res[0] = intervals[0];
int index = 0;
for(int i = 1; i < intervals.length; i++){
int[] curr = intervals[i];
//res 中最后一个元素
int[] last = res[index];
//重叠
if(curr[0] <= last[1]){
//找到最大的end,进行合并
last[1] = Math.max(last[1],curr[1]);
} else {
res[++index] = curr;
}
}
return Arrays.copyOf(res,index+1);
}
}
[986] 区间列表的交集

- 题解
class Solution {
public int[][] intervalIntersection(int[][] firstList, int[][] secondList) {
int i = 0, j = 0;
int n = firstList.length, m = secondList.length;
int[][] res = new int[m+n][2];
int index = -1;
while(i < n && j < m){
int a1 = firstList[i][0], a2 = firstList[i][1];
int b1 = secondList[j][0], b2 = secondList[j][1];
if(b2 >= a1 && b1 <= a2){
// 计算出交集,加入 res
index++;
res[index][0] = Math.max(a1, b1);
res[index][1] = Math.min(a2, b2);
}
if(b2 < a2 ) {
j++;
} else {
i++;
}
}
return Arrays.copyOf(res, index + 1);
}
}
4. 回溯算法
解决⼀个回溯问题,实际上就是⼀个决策树的遍历过程。你只需要思考
3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,⽆法再做选择的条件。
result = []
def backtrack(路径, 选择列表):
if 满⾜结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
[46] 全排列

- 题解
class Solution {
List<List<Integer>> res = new LinkedList<>();
public List<List<Integer>> permute(int[] nums) {
//记录路径
LinkedList<Integer> track = new LinkedList<>();
backTrack(nums, track);
return res;
}
// 路径:记录在 track 中
// 选择列表:nums 中不存在于 track 的那些元素
// 结束条件:nums 中的元素全都在 track 中出现
void backTrack(int[] nums, LinkedList<Integer> track){
// 触发结束条件
if(nums.length == track.size()){
res.add(new LinkedList(track));
return;
}
for(int i = 0; i < nums.length; i++){
// 排除不合法的选择
if(track.contains(nums[i])){
continue;
}
// 做选择
track.add(nums[i]);
// 进⼊下⼀层决策树
backTrack(nums, track);
//取消选择
track.removeLast();
}
}
}
[78] 子集

- 题解
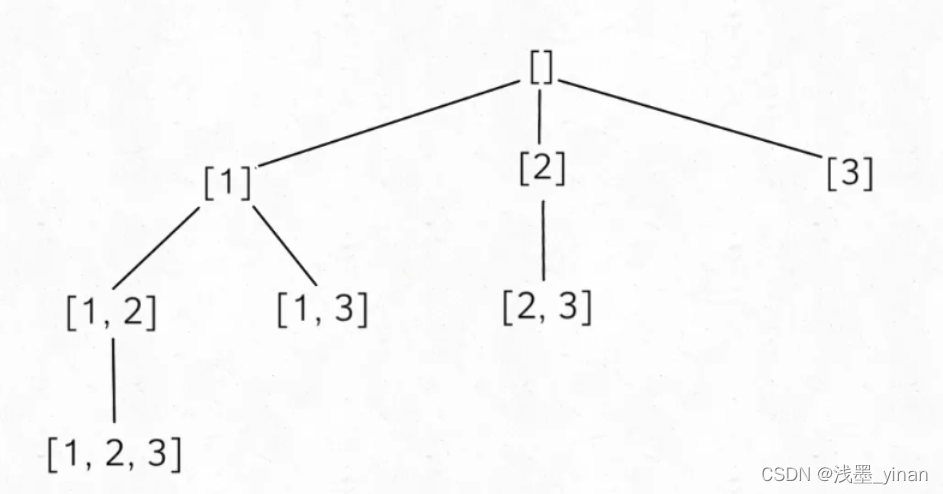
class Solution {
List<List<Integer>> res = new LinkedList<>();
public List<List<Integer>> subsets(int[] nums) {
// 记录走过的路径
LinkedList<Integer> track = new LinkedList<>();
backTrack(nums, 0, track);
return res;
}
void backTrack(int[] nums,int start,LinkedList<Integer> track){
res.add(new LinkedList(track));
// 注意 i 从 start 开始递增
for(int i = start; i < nums.length; i++){
// 做选择
track.add(nums[i]);
// 进⼊下⼀层决策树
backTrack(nums,i + 1 ,track);
//取消选择
track.removeLast();
}
}
}
[77] 组合

- 题解
class Solution {
List<List<Integer>> res = new LinkedList<>();
public List<List<Integer>> combine(int n, int k) {
if(n <= 0 || k <= 0) return res;
LinkedList<Integer> track = new LinkedList<>();
backTrack(n, k, 1, track);
return res;
}
void backTrack(int n, int k, int start, LinkedList<Integer> track){
// 到达树的底部
if(k == track.size()){
res.add(new LinkedList(track));
return;
}
for(int i = start; i <= n; i++){
//做选择
track.add(i);
backTrack(n, k, i + 1, track);
track.removeLast();
}
}
}
5. 高频
[204] 计数质数

- 题解
Sieve of Eratosthenes算法
class Solution {
//Sieve of Eratosthenes算法
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
Arrays.fill(isPrime,true);
for(int i = 2; i * i < n; i++){
if(isPrime[i]){
for(int j = i * i;j < n; j+=i){
isPrime[j] = false;
}
}
}
int count = 0;
for(int i = 2; i < n; i++){
if(isPrime[i]){
count++;
}
}
return count;
}
}
[372] 超级次方

- 题解
(a * b) % k = (a % k)(b % k) % k
对乘法的结果求模,等价于先对每个因子都求模,然后对因子相乘的结果再求模。
class Solution {
int base = 1337;
// 计算 a 的 k 次方然后与 base 求模的结果
int mypow(int a, int k){
//对因子求模
a = a % base;
int res = 1;
for(int i = 0; i < k; i++){
// 这里有乘法,是潜在的溢出点
res *= a;
// 这里有乘法,是潜在的溢出点
res %= base;
}
return res;
}
int compute(int a, int[] b, int n){
if( n == -1) return 1;
int last = b[n];
int part1 = mypow(a, last);
int part2 = mypow(compute(a, b, n - 1), 10);
return (part1 * part2) % base;
}
public int superPow(int a, int[] b) {
if(b.length == 0 || b == null) return 1;
int n = b.length - 1;
return compute(a, b, n);
}
}
[875] 爱吃香蕉的珂珂

- 题解
找出一个能吃完所有香蕉的最小速度,使用二分搜索左侧边界
class Solution {
//找出一个能吃完所有香蕉的最小速度
public int minEatingSpeed(int[] piles, int h) {
// 要求最小速度搜索左侧边界
int left = 1, right = getMax(piles) + 1;
while (left < right){
int mid = left + (right - left) / 2;
if(canFinish(piles, mid, h)){
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
boolean canFinish(int[] piles, int speed, int h){
int time = 0;
for(int n : piles){
time += timeOf(n, speed);
}
return time <= h;
}
//以speed的速度吃香蕉要吃多久
int timeOf(int n, int speed){
return (n / speed) + (n % speed > 0 ? 1 : 0);
}
int getMax(int[] piles){
int max = -1;
for(int n : piles){
max = Math.max(n, max);
}
return max;
}
}
[1011] 在 D 天内送达包裹的能力

- 题解
遍历最小载重和最大载重值,找到可以装载完成的一个最小装载值,采用二分搜索进行优化
class Solution {
//遍历最小载重和最大载重值,找到可以装载完成的一个最小装载值,采用二分搜索进行优化
public int shipWithinDays(int[] weights, int days) {
//装载最小值
int left =0;
//装载最大值
int right = 1;
for(int i = 0; i < weights.length; i++){
left = Math.max(left, weights[i]);
right += weights[i];
}
while (left < right){
int mid = left + (right - left) / 2;
if (canFinish(weights, days, mid)) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
boolean canFinish(int[] weights, int days, int cap) {
int count = 0;
for(int day = 0; day < days; day++){
int maxCap = cap;
while((maxCap -= weights[count]) >= 0 ){
count++;
if(count == weights.length){
return true;
}
}
}
return false;
}
}
[42] 接雨水

- 题解
边走边算左侧的最大值和右侧的最大值,用较小的减去当前的值即为雨水值。
class Solution {
public int trap(int[] height) {
if(height.length == 0) return 0;
int n = height.length;
int left = 0,right = height.length - 1;
int l_max = height[0], r_max = height[n -1];
int res = 0;
while (left < right){
l_max = Math.max(l_max, height[left]);
r_max = Math.max(r_max, height[right]);
if(l_max > r_max){
res += r_max - height[right];
right--;
}else {
res += l_max - height[left];
left++;
}
}
return res;
}
}
[11] 盛最多水的容器

- 题解
用 left 和 right 两个指针从两端向中心收缩,一边收缩一边计算 [left, right] 之间的矩形面积,取最大的面积值即是答案。
class Solution {
public int maxArea(int[] height) {
int left = 0, right = height.length - 1;
int res = 0;
while (left < right) {
//计算矩形面积
int curArea = Math.min(height[left], height[right]) * (right - left);
res = Math.max(curArea, res);
if(height[left] < height[right]){
left++;
} else {
right--;
}
}
return res;
}
}
[15] 三数之和

- 题解
定住一个数转化为求两数之和
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
//数组排序
Arrays.sort(nums);
int n = nums.length;
List<List<Integer>> res = new ArrayList<>();
for(int i = 0; i < n; i++){
//计算TWOSum
List<List<Integer>> tuples = twoSumTarget(nums, i + 1, 0 - nums[i]);
//变为3元组
for(List<Integer> tuple : tuples){
tuple.add(nums[i]);
res.add(tuple);
}
//跳过重复
while(i < n - 1 && nums[i] == nums[i + 1]) i++;
}
return res;
}
List<List<Integer>> twoSumTarget(int[] nums, int start, int target){
// 左指针改为从 start 开始,其他不变
int lo = start, hi = nums.length - 1;
List<List<Integer>> res = new ArrayList<List<Integer>>();
while(lo < hi){
int sum = nums[lo] + nums[hi];
int left = nums[lo], right = nums[hi];
if(sum < target){
while(lo < hi && nums[lo] == left) lo++;
} else if(sum > target){
while(lo < hi && nums[hi] == right) hi--;
System.out.println(hi);
} else {
ArrayList<Integer> temp = new ArrayList<>();
temp.add(left);
temp.add(right);
res.add(temp);
temp = null;
while(lo < hi && nums[lo] == left) lo++;
while(lo < hi && nums[hi] == right) hi--;
}
}
return res;
}
}
BFS相关
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
Queue<Node> q; // 核心数据结构
Set<Node> visited; // 避免走回头路
q.offer(start); // 将起点加入队列
visited.add(start);
int step = 0; // 记录扩散的步数
while (q not empty) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
/* 划重点:这里判断是否到达终点 */
if (cur is target)
return step;
/* 将 cur 的相邻节点加入队列 */
for (Node x : cur.adj())
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
/* 划重点:更新步数在这里 */
step++;
}
}
队列q就不说了,BFS 的核心数据结构;cur.adj()泛指cur相邻的节点,比如说二维数组中,cur上下左右四面的位置就是相邻节点;visited的主要作用是防止走回头路,大部分时候都是必须的,但是像一般的二叉树结构,没有子节点到父节点的指针,不会走回头路就不需要visited。
[111] 二叉树的最小深度

- 题解
class Solution {
public int minDepth(TreeNode root) {
if(root == null) return 0;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
//root 本身就是一层初始化为1
int depth = 1;
while (!q.isEmpty()){
int sz = q.size();
//将当前队列的节点往四周扩散
for(int i = 0; i < sz; i++){
TreeNode cur = q.poll();
//判断是否到达终点
if(cur.left == null && cur.right == null){
return depth;
}
//将cur两端的节点加入队列
if(cur.left != null){
q.offer(cur.left);
}
if(cur.right != null){
q.offer(cur.right);
}
}
depth++;
}
return depth;
}
}
DFS相关
[200] 岛屿数量

class Solution {
public int numIslands(char[][] grid) {
int res = 0;
int m = grid.length, n = grid[0].length;
//遍历grid
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid[i][j] == '1'){
//每发现一个岛屿,岛屿数量加一
res++;
// 然后使用DFS将岛屿淹没了
dfs(grid, i, j);
}
}
}
return res;
}
// 将与[i, j]相连的陆地变为海水
void dfs(char[][] grid, int i, int j){
int m = grid.length, n = grid[0].length;
if(i < 0 || j < 0 || i >= m || j >= n){
return;
}
if(grid[i][j] == '0'){
//已经是海水
return;
}
//将i,j变为海水
grid[i][j] = '0';
// 淹没上下左右的土地
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
}
}
[1254] 统计封闭岛屿的数目

- 题解
把靠边的陆地淹掉,然后去数剩下的陆地数量就⾏了
class Solution {
public int closedIsland(int[][] grid) {
int m = grid.length, n = grid[0].length;
int res = 0;
//将上方变为海水
for(int i = 0; i < n; i++){
dfs(grid, 0, i);
}
//将上方变为海水
for(int i = 0; i < n; i++){
dfs(grid, m - 1, i);
}
//将左侧变为海水
for(int i = 0; i < m; i++){
dfs(grid, i, 0);
}
//将右侧变为海水
for(int i = 0; i < m; i++){
dfs(grid, i, n - 1);
}
//求封闭岛屿
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid[i][j] == 0){
res++;
//将周围变为海水
dfs(grid, i, j);
}
}
}
return res;
}
void dfs(int[][] grid, int i, int j){
int m = grid.length, n = grid[0].length;
if(i < 0 || j < 0 || i >= m || j >= n){
return;
}
if (grid[i][j] == 1) {
return;
}
//将i,j变为海水
grid[i][j] = 1;
//将上下左右变为海水
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
}
}
1020. 飞地的数量

- 题解
class Solution {
public int numEnclaves(int[][] grid) {
int m = grid.length, n = grid[0].length;
//将边界变为海水
for(int i = 0; i < n; i ++){
dfs(grid, 0, i);
dfs(grid, m - 1, i);
}
for(int i = 0; i < m; i++){
dfs(grid, i, 0);
dfs(grid, i, n - 1);
}
//岛屿的数量
int res = 0;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid[i][j] == 1){
res++;
}
}
}
return res;
}
void dfs(int[][] grid, int i, int j) {
int m = grid.length, n = grid[0].length;
if (i < 0 || j < 0 || i >= m || j >= n) {
return;
}
//如果已经是海水直接返回
if (grid[i][j] == 0) {
return;
}
//将i,j变为海水
grid[i][j] = 0;
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
}
}
695. 岛屿的最大面积
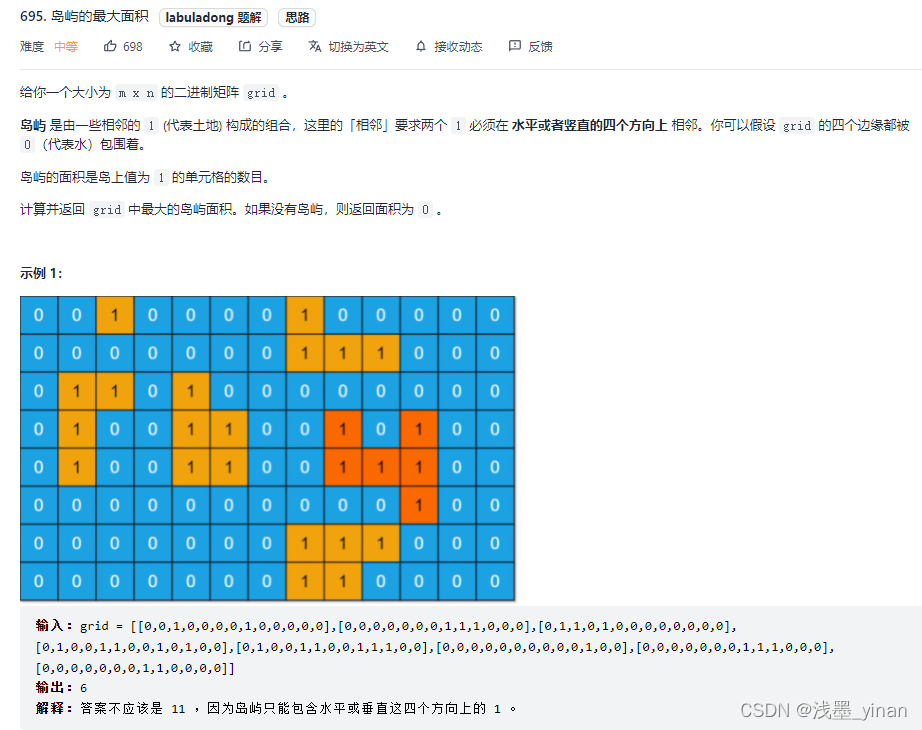
- 题解
class Solution {
public int maxAreaOfIsland(int[][] grid) {
int m = grid.length, n = grid[0].length;
int res = 0;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid[i][j] == 1){
res = Math.max(res, dfs(grid, i, j));
}
}
}
return res;
}
int dfs (int[][] grid, int i, int j) {
int m = grid.length, n = grid[0].length;
if(i < 0 || j < 0 || i >= m || j >= n){
return 0;
}
if (grid[i][j] == 0) {
return 0;
}
//变为海水
grid[i][j] = 0;
//计算i,j相邻的土地的面积
return dfs(grid, i + 1, j) +
dfs(grid, i - 1, j) +
dfs(grid, i, j + 1) +
dfs(grid, i, j - 1) + 1;
}
}
1905. 统计子岛屿

- 题解
class Solution {
public int countSubIslands(int[][] grid1, int[][] grid2) {
int m = grid1.length, n = grid1[0].length;
//排除grid1中为0,grid2为1的,此时一定不为子岛屿
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid1[i][j] == 0 && grid2[i][j] == 1){
dfs(grid2, i, j);
}
}
}
int res = 0;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j ++){
if(grid2[i][j] == 1) res++;
dfs(grid2, i, j);
}
}
return res;
}
//dfs的主要目的是将i,j以及相邻的岛屿变为0
void dfs(int[][] grid, int i, int j){
int m = grid.length, n = grid[0].length;
if(i < 0 || j < 0 || i >= m || j >= n){
return;
}
if(grid[i][j] == 0) return;
//将i,j变为水域
grid[i][j] = 0;
//将i,j以及相邻的岛屿变为水域
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
dfs(grid, i, j - 1);
dfs(grid, i, j + 1);
}
}
694. 不同岛屿的数量
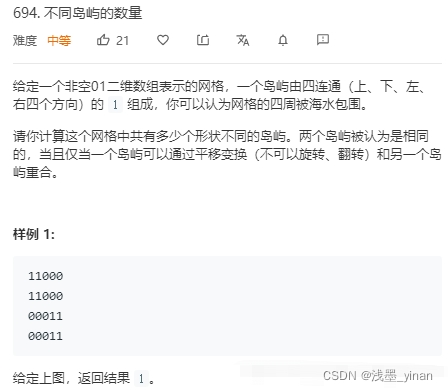
- 题解
每次使⽤ dfs 遍历岛屿的时候⽣成这串数字进⾏⽐较,就可以计算到底有多少个不同的岛屿了。
public class Solution {
int numDistinctIslands(int[][] grid) {
int m = grid.length, n = grid[0].length;
HashSet<String> res = new HashSet<>();
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid[i][j] == 1){
StringBuilder sb = new StringBuilder();
dfs(grid, i, j, sb, 666);
res.add(sb.toString());
}
}
}
return res.size();
}
void dfs(int grid[][], int i, int j, StringBuilder sb, int dir){
int m = grid.length,n = grid[0].length;
if(i < 0 || j < 0 || i >= m || j >=n || grid[i][j] == 0){
return;
}
//前序遍历进入i,j淹没并正向记录
grid[i][j] = 0;
sb.append(dir).append(',');
dfs(grid, i + 1, j, sb, 1);
dfs(grid, i - 1, j, sb, 2);
dfs(grid, i, j + 1, sb, 3);
dfs(grid, i, j - 1, sb, 4);
//后序遍历反向离开
sb.append(-dir).append(',');
}
}
图
797. 所有可能的路径

- 题解
解法很简单,以 0 为起点遍历图,同时记录遍历过的路径,当遍历到终点时将路径记录下来即可
class Solution {
List<List<Integer>> res = new LinkedList<>();
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
//维护递归过程经过的路径
LinkedList<Integer> path = new LinkedList<>();
traverse(graph, 0, path);
return res;
}
//图的遍历
void traverse(int[][] graph, int s, LinkedList<Integer> path){
path.addLast(s);
int n = graph.length;
if(s == n - 1){
//到达终点
res.add(new LinkedList<>(path));
path.removeLast();
return;
}
//递归每个节点
for(int v : graph[s]){
traverse(graph, v, path);
}
path.removeLast();
}
}
207. 课程表

- 题解
看到依赖问题,⾸先想到的就是把问题转化成「有向图」这种数据结构,只要图中存在环,那就说明存在循环依赖。
如果发现这幅有向图中存在环,那就说明课程之间存在循环依赖,肯定没办法全部上完;反之,如果没有环,那么肯定能上完全部课程。
class Solution {
//建有向图
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites){
//图中的节点
List<Integer>[] graph = new LinkedList[numCourses];
for(int i = 0; i < numCourses; i++){
graph[i] = new LinkedList<>();
}
for(int[] edge : prerequisites){
//1是起点吗,0是终点
int from = edge[1], to = edge[0];
graph[from].add(to);
}
return graph;
}
//记录⼀次递归堆栈中的节点
boolean[] onPath;
// 记录遍历过的节点,防⽌⾛回头路
boolean[] visited;
// 记录图中是否有环
boolean hasCycle = false;
public boolean canFinish(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
visited = new boolean[numCourses];
onPath = new boolean[numCourses];
//只要没有循环依赖可以完成所有课程
for(int i = 0; i < numCourses; i++){
traverse(graph, i);
}
return !hasCycle;
}
void traverse(List<Integer>[] graph, int s){
//表示以该节点遍历的路径出现了环
if(onPath[s]){
hasCycle = true;
}
// 如果已经找到了环,也不⽤再遍历了
if(visited[s] || hasCycle){
return;
}
//前序代码位置
visited[s] = true;
onPath[s] = true;
for(int t : graph[s]){
traverse(graph, t);
}
onPath[s] = false;
}
}
210. 课程表 II

- 题解
后序遍历的结果进⾏反转,就是拓扑排序的结果
class Solution {
boolean[] onPath, visited;
// 记录是否存在环
boolean hasCycle = false;
List<Integer> postOrder = new ArrayList<>();
public int[] findOrder(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
onPath = new boolean[numCourses];
visited = new boolean[numCourses];
// 遍历图
for(int i = 0; i < numCourses; i++){
traverse(graph, i);
}
// 有环图⽆法进⾏拓扑排序
if(hasCycle) {
return new int[]{};
}
// 逆后序遍历结果即为拓扑排序结果
Collections.reverse(postOrder);
int[] res = new int[numCourses];
for(int i = 0; i < numCourses; i++){
res[i] = postOrder.get(i);
}
return res;
}
//建立有向图
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites){
List<Integer>[] graph = new LinkedList[numCourses];
for(int i = 0; i < numCourses; i++){
graph[i] = new LinkedList<>();
}
for(int[] t : prerequisites){
int from = t[1], to = t[0];
graph[from].add(to);
}
return graph;
}
void traverse(List<Integer>[] graph, int i){
if(onPath[i]){
hasCycle = true;
}
if(visited[i] || hasCycle){
return;
}
visited[i] = true;
onPath[i] = true;
for(int t : graph[i]){
traverse(graph, t);
}
onPath[i] = false;
postOrder.add(i);
}
}


























 836
836

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








