educoder算法设计与分析实验五回溯法拓展2

这篇博客介绍了如何使用非递归和递归算法解决棋盘上的皇后问题，以及如何构造一个使得相邻两数之和为素数的数环。内容包括具体的问题描述、预期输出以及示例代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

实验五回溯法拓展2

第1关：非递归实现皇后问题
第2关：递归算法解决皇后问题
第3关：素数圈

第1关：非递归实现皇后问题

题目描述：

本关任务：在n×n格的棋盘上放置彼此不受攻击的 n 个皇后。按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。用非递归算法解决该问题。

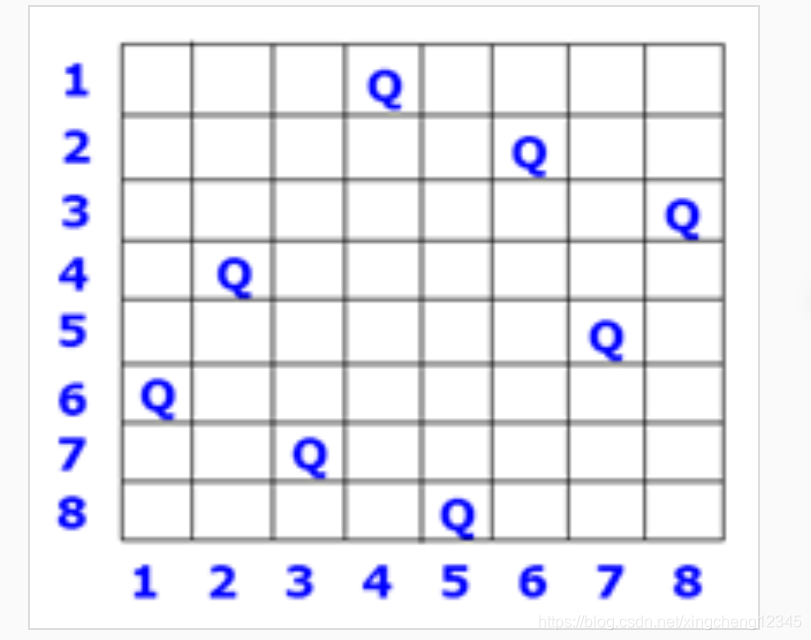
下图是一个 8 个皇后的例子，8 个皇后彼此不受攻击。

在这里插入图片描述

测试输入:

4（皇后的数目）

预期输出：

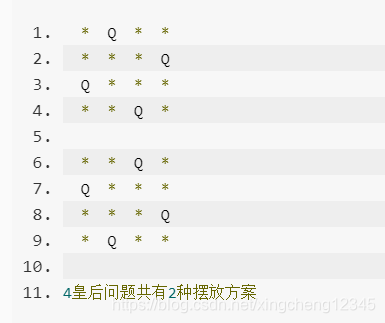
在这里插入图片描述

分析：
无
　　
代码实现：

#include <stdio.h>

/**********  Begin  **********/
int count = 0;
void output(int a[], int n)
{
   
   
    for (int i = 0; i < n; i++)
    {
   
   
        for (int j = 0; j < n; j++)
        {
   
   
            if (j == a[i] - 1)
            {
   
   
                printf("  Q");
            }
            else
            {
   
   
                printf("  *");
            }
        }
        printf("\n");
    }
    printf("\n");
    count++;
}

int check(int a[], int k)
{
   
   
    int i;
    for (i = 0; i <= k - 1; i++)
    {
   
   
        if (a[i] == a[k] || (a[i] - a[k] == i - k || a[i] - a[k] == k - i))
        {
   
   
            return 0;
        }
    }
    return 1;
}

void find(int a[], int n)
{
   
   
    int k = 0;
    a