一、拓扑排序
设G=<V,E>是一个具有n个顶点的有向图,V中的顶点序列v1,v2,v3,...,vn称为一个拓扑序列。若<vi,vj>是图中的一条边或者从顶点vi到顶点vj有路径,则在该序列中顶点vi必须排在顶点vj之前。
在一个有向图中找一个拓扑序列的过程称为拓扑排序。
用顶点表示活动,用有向边表示活动之间的优先关系的有向图称为顶点表示活动的网。
拓扑排序方法如下:
1、从有向图中选择一个没有前驱(即入度为0)的顶点并且输出它。
2、从图中删去该顶点,并且删去从该顶点发出的全部有向边。
3、重复上述两步,直到剩余的图中不再存在没有前驱的顶点为止。
这样的操作结果有两种:一种是图中全部顶点都被输出,即该图中所有顶点都在其拓扑序列中,这说明图中不存在回路;另一种是图中顶点未被全部输出,这说明图中存在回路。所以可以通过对一个有向图进行拓扑排序,看是否产生全部顶点的拓扑序列来确定该图中是否存在回路。
二、AOE网与关键路径
有向无环图描述工程的预计进度,以顶点表示事件,有向边表示活动,边e的权c(e)表示完成活动e所需的时间,或者说活动e持续时间。图中入度为0的顶点表示工程的开始事件,出度为0的顶点表示工程结束事件,称这样的有向图为边表示活动的网(AOE网)。
通常每个工程都只有一个开始事件和一个结束事件,因此表示工程的AOE网都只有一个入度为0的顶点,称为源点,和一个出度为0的顶点,称为汇点。如果图中存在多个入度为0的顶点,只要加一个虚拟源点,使这个虚拟源点到原来所有入度为0的点都有一条长度为0的边,从而变成只有一个源点。对存在多个出度为0的顶点的情况做类似的处理。只讨论单源点和单汇点的情况。
利用这样的AOE网能够计算完成整个工程预计需要多少时间,并找出影响工程进度的“关键活动”,从而为决策者提供修改各活动的预计进度的依据。
在AOE网中,从源点到汇点的所有路径中具有最大路径长度的路径称为关键路径。完成整个工程的最短时间就是AOE网中关键路径的长度,或者说是AOE网中一条关键路径上各活动持续时间的总和,把关键路径上的活动称为关键活动。关键活动不存在富余的时间,而非关键活动可能存在富余的时间。通常一个AOE网可能存在多条关键路径,但它们的长度是相同的。
因此,只要找出AOE网中的所有关键活动也就找到了全部的关键路径。
/**
* 实验题目:
* 求AOE网中的所有关键活动
* 实验目的:
* 领会拓扑排序和AOE网中关键路径的求解过程及其算法设计
* 实验内容:
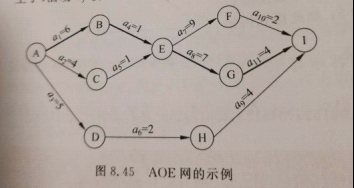
* 设计程序,求如下图8.45所示的AOE网的所有关键活动
*/
#include <stdio.h>
#include <malloc.h>
#include <stdbool.h>
#define INF 32767 //定义∞
#define MAXV 100 //最大顶点个数
typedef char InfoType;
/*-------------------------以下定义邻接矩阵类型---------------------------*/
typedef struct
{
int no; //顶点编号
InfoType info; //顶点信息
}VertexType; //顶点类型
typedef struct
{
int edges[MAXV][MAXV]; //邻接矩阵数组(用一个二维数组存放顶点间关系(边或弧)的数据)
int n; //顶点数
int e; //边数
VertexType vexs[MAXV]; //存放顶点信息(用一个一维数组存放图中所有顶点数据)
}MatGraph; //完整的图邻接矩阵类型
//邻接表表示法-将每个顶点的邻接点串成一个单链表
/*-----------以下定义邻接表类型--------------*/
typedef struct ArcNode
{
int adjvex; //该边的邻接点编号
struct ArcNode *nextarc; //指向下一条边的指针
int weight; //该边的相关信息,如权值(用整型表示)
}ArcNode; //边结点类型
typedef struct VNode
{
InfoType info; //顶点其他信息
int cnt; //存放顶点入度,仅用于拓扑排序
ArcNode *firstarc; //指向第一条边
}VNode; //邻接表结点类型
typedef struct
{
VNode adjlist[MAXV]; //邻接表头结点数组
int n; //图中顶点数
int e; //图中边数
}AdjGraph; //完整的图邻接表类型
/*-------------------------邻接矩阵的基本运算算法---------------------------*/
/*------------由边数组A、顶点数n和边数e创建图的邻接矩阵g--------------------*/
void CreateMat(MatGraph &g, int A[MAXV][MAXV], int n, int e)
{
int i, j;
g.n = n;
g.e = e;
for(i = 0; i < g.n; i++)
for(j = 0; j < g.n; j++)
g.edges[i][j] = A[i][j];
}
/*------------输出邻接矩阵g--------------------*/
void DispMat(MatGraph g)
{
int i, j;
for(i = 0; i < g.n; i++)
{
for(j = 0; j < g.n; j++)
{
if(g.edges[i][j] != INF)
printf("%4d", g.edges[i][j]);
else
printf("%4s", "∞");
}
printf("\n");
}
}
/*-------------------------邻接表的基本运算算法---------------------------*/
/*-------------------由边数组A、顶点数n和边数e创建图的邻接表G--------------------*/
void CreateAdj(AdjGraph *&G, int A[MAXV][MAXV], int n, int e)
{
int i, j;
ArcNode *p;
G = (AdjGraph *)malloc(sizeof(AdjGraph));
for(i = 0; i < n; i++) //给邻接表中所有头结点的指针域置初值NULL
{
G->adjlist[i].firstarc = NULL;
}
for(i = 0; i < n; i++) //检查邻接矩阵中的每个元素
{
for(j = n - 1; j >= 0; j--)
{
if(A[i][j] != 0 && A[i][j] != INF) //存在一条边
{
p = (ArcNode *)malloc(sizeof(ArcNode)); //创建一个结点p
p->adjvex = j; //邻接点编号
p->weight = A[i][j]; //边的权重
p->nextarc = G->adjlist[i].firstarc; //采用头插法插入结点p
G->adjlist[i].firstarc = p;
}
}
}
G->n = n;
G->e = e;
}
/*-------------------输出邻接表G--------------------*/
void DispAdj(AdjGraph *G)
{
ArcNode *p;
for(int i = 0; i < G->n; i++)
{
p = G->adjlist[i].firstarc;
printf("顶点%d: ", i);
while(p != NULL)
{
printf("%3d[%d]->", p->adjvex, p->weight); //邻接点编号[权重]
p = p->nextarc;
}
printf("∧\n");
}
}
/*-------------------销毁图的邻接表G--------------------*/
void DestroyAdj(AdjGraph *&G)
{
ArcNode *pre, *p;
for(int i = 0; i < G->n; i++)
{
pre = G->adjlist[i].firstarc; //pre指向第i个单链表的首结点
if(pre != NULL)
{
p = pre->nextarc;
while(p != NULL) //释放第i个单链表的所有边结点
{
free(pre);
pre = p;
p = p->nextarc;
}
free(pre);
}
}
free(G); //释放头结点数组
}
typedef struct KeyNode{
int ino; // 起点
int eno; // 终点
}KeyNode; // 关键活动类型
/*---------------------由含有n个顶点的有向图G产生一个拓扑序列--------------------*/
static bool TopSort(AdjGraph *G, int topseq[])
{
int i;
int j; // 循环变量
int n = 0; // 拓扑序列的个数
int st[MAXV]; // 定义一个顺序栈
int top = -1; // 栈顶指针为top
ArcNode *p; // 边结点类型的指针
/*--------------所有顶点的入度设置初值0-------------------*/
for(i = 0; i < G->n; i++)
G->adjlist[i].cnt = 0;
/*---------------求所有顶点的入度--------------------*/
for(i = 0; i < G->n; i++){
p = G->adjlist[i].firstarc;
while(p != NULL){
G->adjlist[p->adjvex].cnt++;
p = p->nextarc;
}
}
for(i = 0; i < G->n; i++) {
if(G->adjlist[i].cnt == 0){ // 入度为0的顶点进栈
top++;
st[top] = i;
}
}
while(top > -1){ // 栈不为空时循环
i = st[top]; // 出栈
top--;
topseq[n] = i;
n++;
p = G->adjlist[i].firstarc; // 找第一个邻接点
while(p != NULL){
j = p->adjvex;
G->adjlist[j].cnt--;
if(G->adjlist[j].cnt == 0){ // 入度为0的相邻顶点进栈
top++;
st[top] = j;
}
p = p->nextarc; // 找下一个邻接点
}
}
if(n < G->n)
return false; // 拓扑序列中不含所有顶点时
else {
printf("拓扑序列:");
for(i = 0; i < n; i++) {
printf("%c ", (char)(topseq[i] + 'A'));
}
printf("\n");
return true;
}
}
/*---------------------从图邻接表G中求出从源点inode到汇点enode的关键活动[0...d]----------------------*/
static bool KeyPath(AdjGraph *G, int &inode, int &enode, KeyNode keynode[], int &d) // 引用类型
{
int i, w;
ArcNode *p;
int topseq[MAXV]; // 用于存放拓扑序列
int ve[MAXV]; // 事件的最早开始时间
int vl[MAXV]; // 事件的最迟开始时间
if(!TopSort(G, topseq)) // 不能产生拓扑序列时返回false
return false;
inode = topseq[0]; // 求出源点
enode = topseq[G->n - 1]; // 求出汇点
for(i = 0; i < G->n; i++) // 先将所有事件的ve置初值为0
ve[i] = 0;
for(i = 0; i < G->n; i++) { // 从左向右求所有事件的最早开始时间
p = G->adjlist[i].firstarc;
while(p != NULL) { // 遍历每一条边即活动
w = p->adjvex;
if(ve[i] + p->weight > ve[w]) // 求最大者
ve[w] = ve[i] + p->weight;
p = p->nextarc;
}
}
for(i = 0; i < G->n; i++) // 先将所有事件的vl值置为最大值
vl[i] = ve[enode];
for(i = G->n - 2; i >= 0; i--){ // 从右向左求所有事件的最迟开始时间
p = G->adjlist[i].firstarc;
while(p != NULL){
w = p->adjvex;
if(vl[w] - p->weight < vl[i]) // 求最小者
vl[i] = vl[w] - p->weight;
p = p->nextarc;
}
}
d = -1; // d存放keynode中的关键活动下标,置初值为-1
for(i = 0; i < G->n; i++) { // 求关键活动
p = G->adjlist[i].firstarc;
while(p != NULL){
w = p->adjvex;
if(ve[i] == vl[w] - p->weight){
d++;
keynode[d].ino = i;
keynode[d].eno = w;
}
p = p->nextarc;
}
}
return true;
}
/*---------------------输出图G的关键活动----------------------*/
static void DispKeynode(AdjGraph *G)
{
int inode, enode, d, i;
KeyNode keynode[MAXV];
if(KeyPath(G, inode, enode, keynode, d)){
printf("从源点%c到汇点%c的关键活动:", char(inode = 'A'), char(enode + 'A'));
for(i = 0; i <= d; i++)
printf("(%c,%c) ", char(keynode[i].ino + 'A'), char(keynode[i].eno + 'A'));
printf("\n");
}else
printf("不能求关键活动\n");
}
int main(void)
{
AdjGraph *G;
int n = 9; // 顶点数
int e = 11; // 边数
int A[MAXV][MAXV] = { // 建立如图8.45的邻接表
{0, 6, 4, 5, INF, INF, INF, INF, INF}/*A*/,{INF, 0, INF, INF, 1, INF, INF, INF, INF}/*B*/,
{INF, INF, 0, INF, 1, INF, INF, INF, INF}/*C*/, {INF, INF, INF, 0, INF, INF, INF, 2, INF}/*D*/,
{INF, INF, INF, INF, 0, 9, 7, INF, INF}/*E*/, {INF, INF, INF, INF, INF, 0, INF, INF, 2}/*F*/,
{INF, INF, INF, INF, INF, INF, 0, INF, 4}/*G*/, {INF, INF, INF, INF, INF, INF, INF, 0, 4}/*H*/,
{INF, INF, INF, INF, INF, INF, INF, INF, 0}/*I*/
};
printf("建立图的邻接表:\n");
CreateAdj(G, A, n, e);
printf("图G的邻接表:\n");
DispAdj(G);
DispKeynode(G); // 求构成关键路径的关键活动
DestroyAdj(G);
return 0;
}
测试结果:
建立图的邻接表:
图G的邻接表:
顶点0: 1[6]-> 2[4]-> 3[5]->∧
顶点1: 4[1]->∧
顶点2: 4[1]->∧
顶点3: 7[2]->∧
顶点4: 5[9]-> 6[7]->∧
顶点5: 8[2]->∧
顶点6: 8[4]->∧
顶点7: 8[4]->∧
顶点8: ∧
拓扑序列:A D H C B E G F I
从源点A到汇点I的关键活动:(A,B) (B,E) (E,F) (E,G) (F,I) (G,I)





















 1968
1968

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








