图的最小生成树-克鲁斯卡尔算法

最新推荐文章于 2025-05-15 00:08:41 发布

静能生悟

最新推荐文章于 2025-05-15 00:08:41 发布

阅读量3.9k

点赞数 2

CC 4.0 BY-SA版权

分类专栏：数据结构与算法

本文链接：https://blog.youkuaiyun.com/xiezhi123456/article/details/88043365

本文介绍了图的最小生成树的概念，并详细讲解了克鲁斯卡尔算法的原理和实现过程，包括如何通过边的权值递增顺序选择合适的边构建最小生成树。示例代码展示了如何在C语言中应用克鲁斯卡尔算法处理邻接矩阵表示的图。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、基本概念

生成树：一个连通图的生成树是一个极小的连通子图，它含有图中全部的顶点，但只有足以构成一棵树的n-1条边。

最小生成树：把构造连通网的最小代价生成树称为最小生成树。（一棵生成树的代价就是树上各边的代价之和）。

二、经典算法

克鲁斯卡尔算法（主要针对边来展开，边数少时效率会非常高，所以对于稀疏图有很大的优势）

1、主要思路，如下图所示：

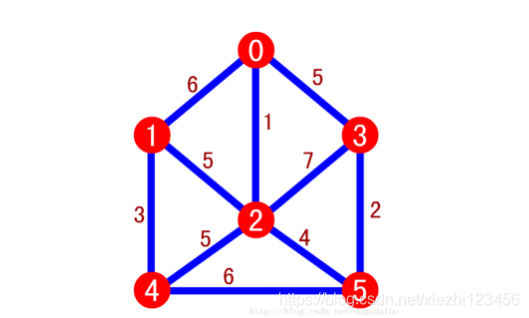
按权值递增的顺序将连接了两棵树的边 (0，2)，(3，5)，(1，4)，(2，5) 依次改为红边，加入 T 中。

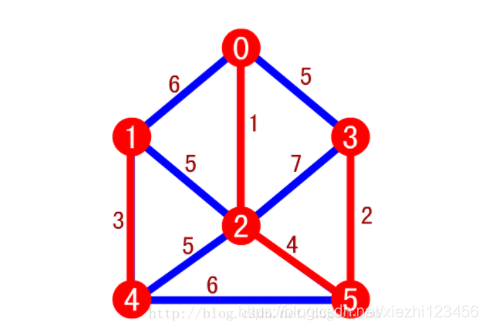
由于边 (0，3) 的两个顶点在相同的一棵树上，所以舍去。而边 (2，4) 和 (1，2) 的长度相同，可以任选其中一条加入。

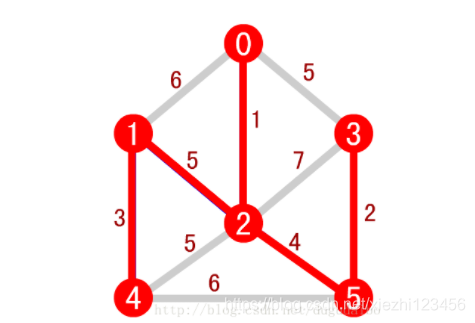
如上图所示，红色连接的部分就是生成的最小生成树。

2、算法实现

/**
* 实验题目:
* 采用克鲁斯卡尔算法求最小生成树
* 实验目的:
* 领会克鲁斯卡尔算法求带权连通图中最小生成树的过程和相关算法设计
* 实验内容:
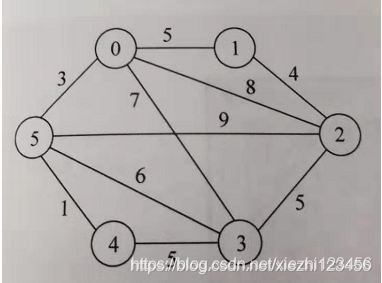
* 编写程序，实现求带权连通图最小生成树的克鲁斯卡尔算法。对于如下
* 图所示的带权连通图，输出从顶点0出发的一颗最小生成树。
*/

#include <stdio.h>
#include <malloc.h>

#define INF 32767 //定义∞
#define MAXV 100 //最大顶点个数

typedef char InfoType;
/*-------------------------以下定义邻接矩阵类型---------------------------*/
typedef struct
{
int no; //顶点编号
InfoType info; //顶点信息
}VertexType; //顶点类型

typedef struct
{
int edges[MAXV][MAXV]; //邻接矩阵数组(用一个二维数组存放顶点间关系(边或弧)的数据)
int n; //顶点数
int e; //边数
VertexType vexs[MAXV]; //存放顶点信息(用一个一维数组存放图中所有顶点数据)
}MatGraph; //完整的图邻接矩阵类型

//邻接表表示法-将每个顶点的邻接点串成一个单链表
/*-----------以下定义邻接表类型--------------*/
typedef struct ArcNode
{
int adjvex; //该边的邻接点编号
struct ArcNode *nextarc; //指向下一条边的指针
int weight; //该边的相关信息,如权值(用整型表示)
}ArcNode; //边结点类型

typedef struct VNode
{
InfoType info;