过拟合问题
过度拟合:就是我们拟合一个高阶多项式,这个假设函数几乎可以拟合所有的数据,但是这个假设函数太过庞大,数量太大导致我们没有足够的数据去约束它。
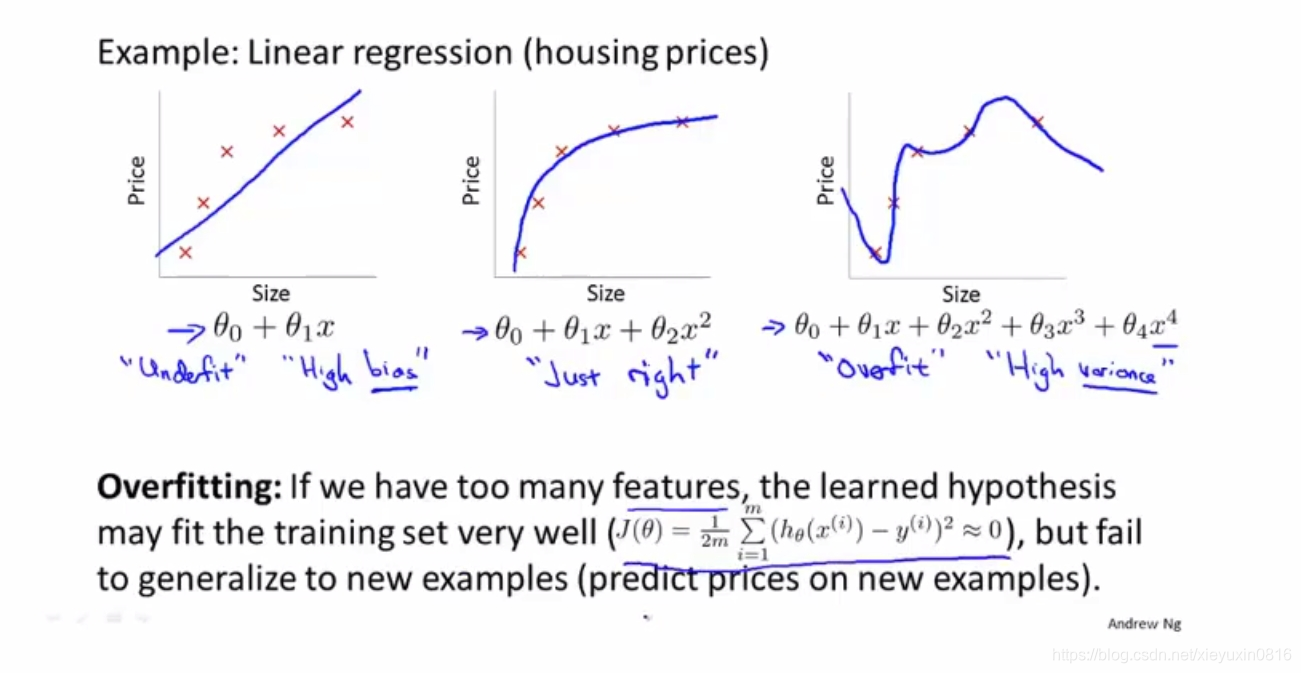 这幅图是以线性回归为例子,第一张图是欠拟合(高偏差),可以看出来它没有很好的拟合数据。第二张图拟合效果刚刚好。第三张图,就是过度拟合(高方差)。
这幅图是以线性回归为例子,第一张图是欠拟合(高偏差),可以看出来它没有很好的拟合数据。第二张图拟合效果刚刚好。第三张图,就是过度拟合(高方差)。
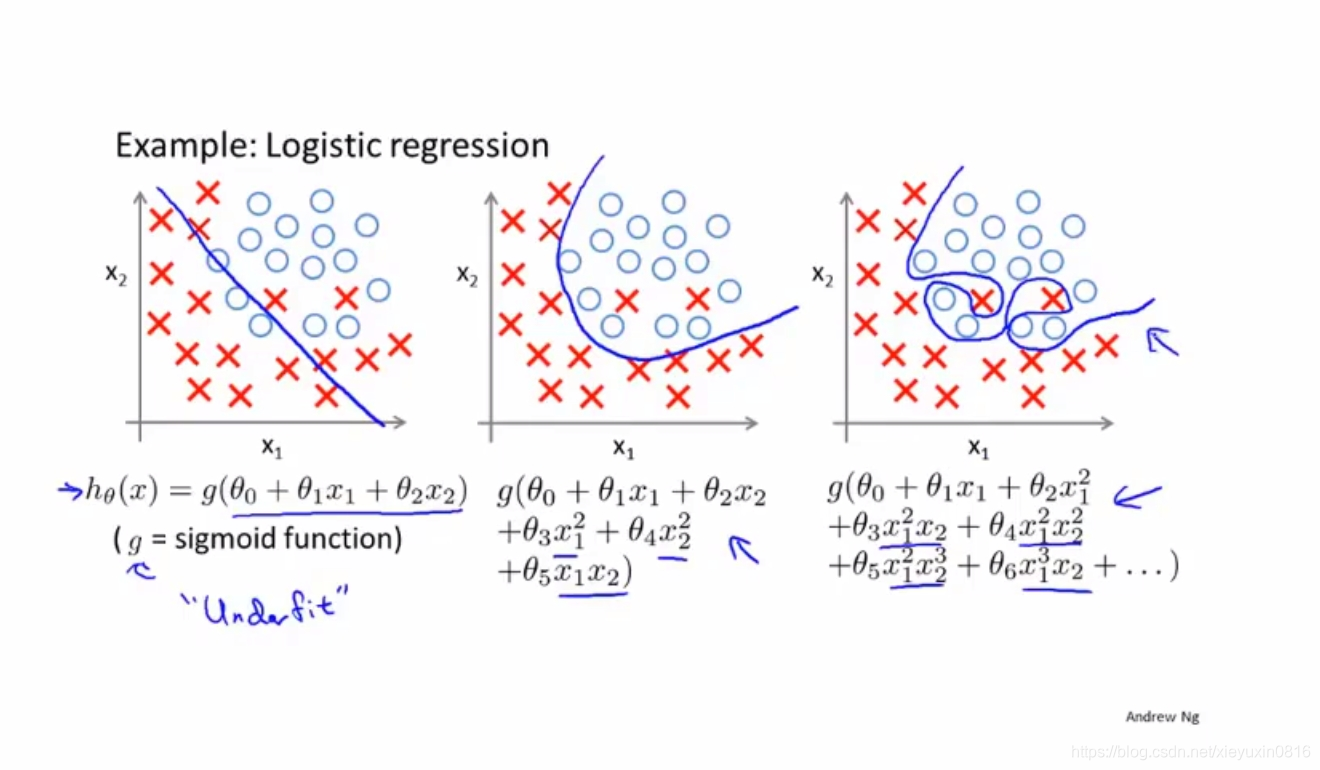 这幅图是以逻辑回归为例子,同样是欠拟合、恰好拟合、和过度拟合。
这幅图是以逻辑回归为例子,同样是欠拟合、恰好拟合、和过度拟合。
那么怎样解决过度拟合的问题呢?主要有两类方法:
第一类:减少我们选取变量的数量。
第二类:正则化。就是保留所有的特征变量,但是减少它们的量级或者参数的大小。(适合每一个变量都有用的情况)
正则化
我们刚刚提到正则化,那么怎样进行正则化呢?我的理解就是在代价函数后加一个惩罚函数,这个惩罚函数会有求我们的参数尽可能的小,这样我们的假设函数就会尽可能的平滑一点。
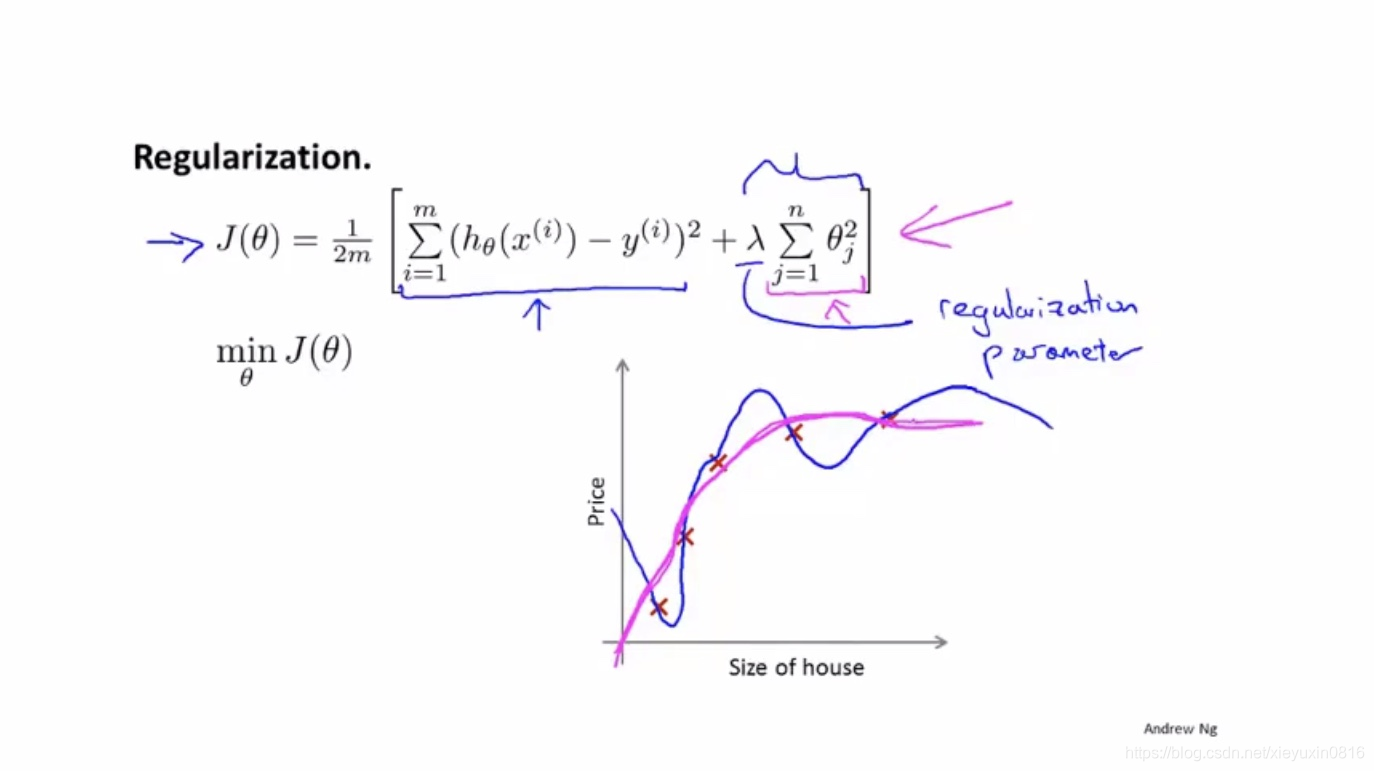 其中拉姆达,我们称之为正则化参数,它可以用来控制不同目标之间的取舍。它如果取值过大就会造成欠拟合。
其中拉姆达,我们称之为正则化参数,它可以用来控制不同目标之间的取舍。它如果取值过大就会造成欠拟合。

线性回归的正则化
梯度下降法

 正规方程法
正规方程法
 正规方程法之前提到过有可能XTX的矩阵会不可逆,但是正则化之后矩阵一定可逆。
正规方程法之前提到过有可能XTX的矩阵会不可逆,但是正则化之后矩阵一定可逆。

逻辑回归的正则化
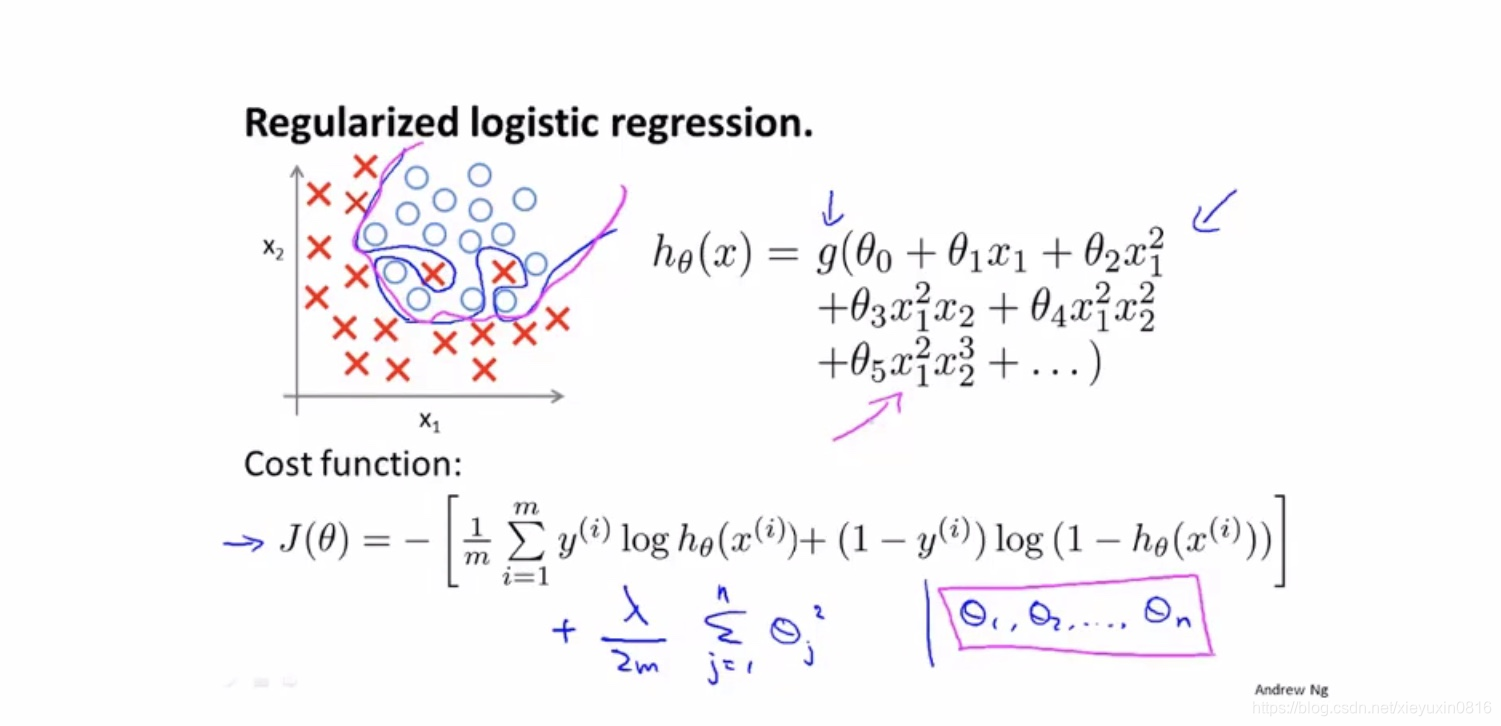






 本文探讨了过拟合问题及其在线性回归和逻辑回归中的表现,提出了解决过拟合的两种主要方法:减少变量数量和正则化。正则化通过在代价函数中加入惩罚项,促使参数更小,从而降低模型复杂度。介绍了线性回归和逻辑回归的正则化实现,包括梯度下降法和正规方程法的应用。
本文探讨了过拟合问题及其在线性回归和逻辑回归中的表现,提出了解决过拟合的两种主要方法:减少变量数量和正则化。正则化通过在代价函数中加入惩罚项,促使参数更小,从而降低模型复杂度。介绍了线性回归和逻辑回归的正则化实现,包括梯度下降法和正规方程法的应用。
















 1852
1852

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








