一、过拟合的问题
所谓过拟合,一般是指过度在训练集上进行优化,进而损害了测试集上的泛化能力的现象,具有高方差,对输入的变化更敏感。与之对应的概念是欠拟合,不能很好地适应训练集,使得算法具有高偏差。
下图就是一个典型的回归案例:

第一个模型是一个线性模型,欠拟合,不能很好地适应我们的训练集;第三个模型是一个四次方的模型,过于强调拟合原始数据,而丢失了算法的本质:预测新数据;而中间的模型似乎最合适。
概括地说过拟合的问题将会在变量过多的时候出现,通过学习得到的假设可能能够非常好地适应训练集(代价函数可能非常接近0),但是可能会导致它无法泛化到新的样本中。
分类案例中也存在这样的问题:

解决过拟合的方法有很多,我将其分为三个层面:
- 从模型层面,可以通过 L1/L2 正则化 等方法;
- 从特征层面,可以丢弃一些不能帮助我们正确预测的特征,通过手工筛选或 PCA 等降维方法;
- 从数据层面,可以获取更大的数据集,也可以进行数据增强,通过一定规则来扩充数据。
二、代价函数
正则化是一种能够保留所有特征(不必降维而丢失信息)的有效解决过拟合的方法。其思想是在损失函数上加上某些规则(限制),限制参数的解空间,从而减少求出过拟合参数的可能性。
仍然以多项式回归为例,如果我们的假设函数为:
h
θ
(
x
)
=
θ
0
+
θ
1
x
+
θ
2
x
2
+
θ
3
x
3
+
θ
4
x
4
h_\theta(x) = \theta_0 + \theta_1 x + \theta_2 x^2 + \theta_3 x^3 + \theta_4 x^4
hθ(x)=θ0+θ1x+θ2x2+θ3x3+θ4x4,其中的高阶项
θ
3
,
θ
4
\theta_3,\theta_4
θ3,θ4导致了过拟合问题,那么我们自然希望
θ
3
\theta_3
θ3 和
θ
4
\theta_4
θ4 越小越好。此时,我们只需要对代价函数做出一点修改:
J
(
θ
)
=
1
2
m
[
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
+
1000
θ
3
2
+
10000
θ
4
2
]
J(\theta) = \frac{1}{2m} \left[ \sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2 + 1000\theta_3^2 + 10000\theta_4^2 \right]
J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+1000θ32+10000θ42]
这样当
J
(
θ
)
J(\theta)
J(θ) 取得极值时,
θ
3
\theta_3
θ3 和
θ
4
\theta_4
θ4 都接近于 0,我们也就达到了目的。一般地,我们并不知道究竟应该对哪些参数做出「惩罚」,我们将对所有的特征进行惩罚,并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设:
J
(
θ
)
=
1
2
m
[
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
+
λ
∑
j
=
1
n
θ
j
2
]
J(\theta) = \frac{1}{2m} \left[\sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2 +\lambda \sum_{j=1}^{n} \theta_j^2 \right]
J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2]
其中, λ \lambda λ 是正则化参数, λ ∑ j = 1 n θ j 2 {\lambda} \sum_{j=1}^{n} \theta_j^2 λ∑j=1nθj2 是正则化项。即我们对除了 θ 0 \theta_0 θ0 以外的参数都做「惩罚」,使得曲线更加光滑。如果 λ \lambda λ 很大,意味着正则化项占主要地位,对 θ j \theta_j θj(不包括 θ 0 \theta_0 θ0 )的惩罚程度太大,有可能导致所有的 θ j \theta_j θj(不包括 θ 0 \theta_0 θ0 ) 都太小了而欠拟合;如果 λ \lambda λ 很小,意味着损失函数占主要地位,就有可能过拟合。因此选取合适的正则化参数 λ \lambda λ 是非常重要的,通常要建立验证集进行网格搜索。
为什么代价函数增加了惩罚项可以使高阶项的参数更快减小,从而解决过拟合的问题,可参考:《L2正则化对权重的影响》。
为什么不对 θ 0 \theta_0 θ0 正则化?因为 θ 0 \theta_0 θ0 是人为设置的偏置项,对于输入的变化(训练集 or 测试集)是不敏感的,不对模型的方差产生贡献,即使发生了过拟合,那也与 θ 0 \theta_0 θ0 无关。
此外,根据正则项的形式,又可分为:二次正则项、一般正则项。二次正则项即为前文提到的形式,更一般的形式为 λ ∑ j = 1 n ∣ θ j ∣ q {\lambda} \sum_{j=1}^{n} \vert \theta_j \vert^q λ∑j=1n∣θj∣q,当 q q q 取不同值等高线图的形状为:
从几何空间上来看,损失函数的碗状曲面和正则化项的曲面叠加之后,就是我们要求极值的曲面。特别地,当 q = 1 q=1 q=1 时,称其为 L1 正则化,也叫 Lasso 回归;当 q = 2 q=2 q=2 时,称其为 L2 正则化,也叫岭回归。L2 由于其处处可微的特性,在实际中更常用。
三、正则化线性回归
对于线性回归的求解,我们之前推导了两种学习算法:一种基于梯度下降,一种基于正规方程。
线性回归的含有正则化项的代价函数为:
J
(
θ
)
=
1
2
m
[
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
+
λ
∑
j
=
1
n
θ
j
2
]
=
1
2
m
[
∑
i
=
1
m
(
θ
T
x
(
i
)
−
y
(
i
)
)
2
+
λ
∑
j
=
1
n
θ
j
2
]
\begin{aligned} J(\theta) &= \frac{1}{2m} \left[ \sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2 + \lambda \sum_{j=1}^{n} \theta_j^2 \right] \\ &= \frac{1}{2m} \left[ \sum_{i=1}^{m} \left( \theta^T x^{(i)} - y^{(i)} \right)^2 + \lambda \sum_{j=1}^{n} \theta_j^2 \right] \end{aligned}
J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2]=2m1[i=1∑m(θTx(i)−y(i))2+λj=1∑nθj2]
对其求导:
∂
J
∂
θ
j
=
1
m
∑
i
=
1
m
(
θ
T
x
(
i
)
−
y
(
i
)
)
x
j
(
i
)
+
[
j
≠
0
]
λ
m
θ
j
,
j
=
0
,
1
,
⋯
,
n
\frac{\partial J}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^{m} \left( \theta^T x^{(i)} - y^{(i)} \right) x_j^{(i)} + [j \neq 0] \frac{\lambda}{m} \theta_j, \quad j = 0, 1, \cdots, n
∂θj∂J=m1i=1∑m(θTx(i)−y(i))xj(i)+[j=0]mλθj,j=0,1,⋯,n
所以梯度下降时,整个迭代更新过程为:
θ
0
:
=
θ
0
−
α
∂
J
∂
θ
0
=
θ
0
−
α
1
m
∑
i
=
1
m
(
θ
T
x
(
i
)
−
y
(
i
)
)
x
0
(
i
)
θ
j
:
=
θ
j
−
α
∂
J
∂
θ
j
=
θ
j
−
α
[
1
m
∑
i
=
1
m
(
θ
T
x
(
i
)
−
y
(
i
)
)
x
j
(
i
)
+
λ
m
θ
j
]
=
θ
j
(
1
−
α
λ
m
)
−
α
1
m
∑
i
=
1
m
(
θ
T
x
(
i
)
−
y
(
i
)
)
x
j
(
i
)
,
j
=
1
,
⋯
,
n
\begin{aligned} \theta_0 &:= \theta_0 - \alpha \frac{\partial J}{\partial \theta_0} \\ &= \theta_0 - \alpha \frac{1}{m} \sum_{i=1}^{m} \left( \theta^T x^{(i)} - y^{(i)} \right) x_0^{(i)} \\ \theta_j &:= \theta_j - \alpha \frac{\partial J}{\partial \theta_j} \\ &= \theta_j - \alpha \left[ \frac{1}{m} \sum_{i=1}^{m} \left( \theta^T x^{(i)} - y^{(i)} \right) x_j^{(i)} + \frac{\lambda}{m} \theta_j \right] \\ &= \theta_j \left( 1 - \alpha \frac{\lambda}{m} \right) - \alpha \frac{1}{m} \sum_{i=1}^{m} \left( \theta^T x^{(i)} - y^{(i)} \right) x_j^{(i)}, \quad j = 1, \cdots, n \end{aligned}
θ0θj:=θ0−α∂θ0∂J=θ0−αm1i=1∑m(θTx(i)−y(i))x0(i):=θj−α∂θj∂J=θj−α[m1i=1∑m(θTx(i)−y(i))xj(i)+mλθj]=θj(1−αmλ)−αm1i=1∑m(θTx(i)−y(i))xj(i),j=1,⋯,n
相当于每次迭代先将参数 θ j \theta_j θj 缩小一点,再做原来的梯度下降。 1 − α λ m < 1 1 - \alpha \frac{\lambda}{m} < 1 1−αmλ<1 通常是只比 1 1 1略小一点的数,因为通常学习率 α α α 很小,但 m m m 却很大。
除了梯度下降,我们还可以直接用正规方程,即在数学上解它。为了记号的方便,我们先假定对
θ
0
\theta_0
θ0 也进行「惩罚」。首先将
J
(
θ
)
J(\theta)
J(θ) 写作矩阵形式:
J
(
θ
)
=
1
2
m
[
(
X
θ
−
y
)
T
(
X
θ
−
y
)
+
λ
θ
T
θ
]
=
1
2
m
[
θ
T
X
T
X
θ
−
θ
T
X
T
y
−
y
T
X
θ
+
y
T
y
+
λ
θ
T
θ
]
\begin{aligned} J(\theta) &= \frac{1}{2m} \left[ (X\theta - y)^T (X\theta - y) + \lambda \theta^T \theta \right] \\ &= \frac{1}{2m} \left[ \theta^T X^T X \theta - \theta^T X^T y - y^T X \theta + y^T y + \lambda \theta^T \theta \right] \end{aligned}
J(θ)=2m1[(Xθ−y)T(Xθ−y)+λθTθ]=2m1[θTXTXθ−θTXTy−yTXθ+yTy+λθTθ]
再用 矩阵的求导法则,然后令:
∂
J
∂
θ
=
1
m
[
X
T
X
θ
−
X
T
y
+
λ
θ
]
=
0
\frac{\partial J}{\partial \theta} = \frac{1}{m} \left[ X^T X \theta - X^T y + \lambda \theta \right] = 0
∂θ∂J=m1[XTXθ−XTy+λθ]=0
则:
(
X
T
X
+
λ
)
θ
=
X
T
y
(X^T X + \lambda)\theta = X^T y
(XTX+λ)θ=XTy
解得:
θ
=
(
X
T
X
+
λ
)
−
1
X
T
y
\theta = (X^T X + \lambda)^{-1} X^T y
θ=(XTX+λ)−1XTy
现在把
j
=
0
j = 0
j=0 的特殊情况考虑进去,那么最后的结果就是:
θ
=
(
X
T
X
+
λ
[
0
1
⋱
1
]
(
n
+
1
)
∗
(
n
+
1
)
)
)
−
1
X
T
y
\theta = \left( X^T X + \lambda \begin{bmatrix} 0 & & & \\ & 1 & & \\ & & \ddots & \\ & & & 1 \end{bmatrix}_{(n+1)*(n+1))} \right)^{-1} X^T y
θ=
XTX+λ
01⋱1
(n+1)∗(n+1))
−1XTy
之前我们曾讨论过 X T X X^T X XTX 不可逆的情形,但在加入正则化项后,只要 λ > 0 \lambda > 0 λ>0,就一定可逆。
四、正则化逻辑回归
对于逻辑回归问题,在之前的课程已经学习过两种优化算法:一种是用梯度下降法来优化代价函数,还有一种是更高级的优化算法,这些高级优化算法需要你想办法计算代价函数,以及计算函数的导数。这节课将会介绍如何改进这两种算法,使它们能够应用于正则化逻辑回归中去。
逻辑回归的含有正则化项的代价函数为:
J
(
θ
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
ln
(
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
ln
(
1
−
h
θ
(
x
(
i
)
)
)
]
+
λ
2
m
∑
j
=
1
n
θ
j
2
=
1
m
∑
i
=
1
m
[
y
(
i
)
ln
(
1
+
e
−
θ
T
x
(
i
)
)
+
(
1
−
y
(
i
)
)
ln
(
1
+
e
θ
T
x
(
i
)
)
]
+
λ
2
m
∑
j
=
1
n
θ
j
2
\begin{aligned} J(\theta) &= -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \ln \left( h_\theta \left( x^{(i)} \right) \right) + \left( 1 - y^{(i)} \right) \ln \left( 1 - h_\theta \left( x^{(i)} \right) \right) \right] + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2 \\ &= \frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \ln \left( 1 + e^{-\theta^T x^{(i)}} \right) + \left( 1 - y^{(i)} \right) \ln \left( 1 + e^{\theta^T x^{(i)}} \right) \right] + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2 \end{aligned}
J(θ)=−m1i=1∑m[y(i)ln(hθ(x(i)))+(1−y(i))ln(1−hθ(x(i)))]+2mλj=1∑nθj2=m1i=1∑m[y(i)ln(1+e−θTx(i))+(1−y(i))ln(1+eθTx(i))]+2mλj=1∑nθj2
同样地,对其求导:
∂
J
∂
θ
j
=
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
+
[
j
≠
0
]
λ
m
θ
j
,
j
=
0
,
1
,
⋯
,
n
\frac{\partial J}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right) x_j^{(i)} + [j \neq 0] \frac{\lambda}{m} \theta_j, \quad j = 0, 1, \cdots, n
∂θj∂J=m1i=1∑m(hθ(x(i))−y(i))xj(i)+[j=0]mλθj,j=0,1,⋯,n
同样地,梯度下降时,整个迭代更新过程为:
θ
0
:
=
θ
0
−
α
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
0
(
i
)
θ
j
:
=
θ
j
(
1
−
α
λ
m
)
−
α
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
,
j
=
1
,
⋯
,
n
\begin{aligned} \theta_0 &:= \theta_0 - \alpha \frac{1}{m} \sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right) x_0^{(i)} \\ \theta_j &:= \theta_j \left( 1 - \alpha \frac{\lambda}{m} \right) - \alpha \frac{1}{m} \sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right) x_j^{(i)}, \quad j = 1, \cdots, n \end{aligned}
θ0θj:=θ0−αm1i=1∑m(hθ(x(i))−y(i))x0(i):=θj(1−αmλ)−αm1i=1∑m(hθ(x(i))−y(i))xj(i),j=1,⋯,n
看上去同线性回归一样,但是知道 h θ ( x ) = g ( θ T X ) h_\theta(x) = g(\theta^T X) hθ(x)=g(θTX),所以与线性回归不同。
五、代码实现
实现线性回归的正规方程解法比较简洁,构造一个 n + 1 n+1 n+1 阶的类单位矩阵即可。但实现梯度下降解法则会遇到一个问题: θ 0 \theta_0 θ0 的更新与 θ j \theta_j θj 不同步,需要分开计算。
下面以 Coursera 上的二分类数据集 ex2data2.txt 为例,首先看一下数据的分布,代码同上一篇:
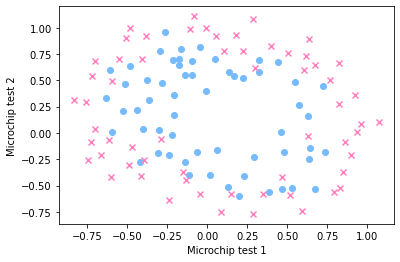
显然,需要引入多项式特征实现高次的曲线,这里将数据的两维都扩充为 6 6 6 次,形成有 28 28 28 维特征的数据,沿用上一篇的矩阵运算,实现逻辑回归如下:
# 导入必要的库
import numpy as np # 用于数值计算和矩阵操作
import matplotlib.pyplot as plt # 用于数据可视化
# 加载数据,数据形状为(118, 3),包含两个特征和一个标签
# 数据格式:[特征1, 特征2, 标签(0或1)]
data = np.loadtxt('ex2data2.txt', delimiter=',')
(m, n) = data.shape # m是样本数量,n是特征数量+1(包含标签)
x1 = data[:, 0].reshape((m, 1)) # 提取第一个特征并重塑为列向量
x2 = data[:, 1].reshape((m, 1)) # 提取第二个特征并重塑为列向量
y = data[:, -1] # 提取标签列
# 映射多项式特征,将低维特征映射到高维,返回X的形状为(118, 28)
# 目的是处理非线性可分的数据,通过增加特征维度来找到决策边界
def map_feature(x1, x2):
# 初始化X为全1列(偏置项)
X = np.ones(x1.size)
# 生成多项式特征,最高次数为6
# 组合形式:x1^i * x2^j,其中i+j从1到6
for i in range(1, 6 + 1):
for j in range(0, i + 1):
# 每次迭代添加新的多项式特征列
X = np.c_[X, np.power(x1, i - j) * np.power(x2, j)]
return X
# 调用函数生成多项式特征矩阵
X = map_feature(x1, x2)
# 设置模型参数
alpha = 0.01 # 学习率,控制梯度下降的步长
lmd = 1 # 正则化参数,防止过拟合
num_iters = 100000 # 梯度下降迭代次数
theta = np.zeros(X.shape[1]) # 初始化参数向量为全0
# 定义sigmoid函数,将线性输出转换为0-1之间的概率
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# 梯度下降算法,用于求解最优参数theta
for _ in range(0, num_iters):
# 计算预测误差:h_theta(x) - y,其中h_theta(x)是sigmoid函数的输出
error = sigmoid(X @ theta) - y # error形状为(118, )
# 更新第一个参数theta[0](不参与正则化,因为它是偏置项)
theta[0] -= (alpha / m) * (X[:,0].T @ error)
# 更新其余参数(参与正则化)
# 正则化项防止参数值过大,避免过拟合
theta[1:] = (1 - alpha * lmd / m) * theta[1:] - (alpha / m) * (X[:,1:].T @ error)
# 绘制散点图展示原始数据
# 找到标签为1的样本索引
pos = np.where(y == 1)[0]
# 找到标签为0的样本索引
neg = np.where(y == 0)[0]
# 绘制正样本,使用圆形标记,天蓝色
plt.scatter(X[pos, 1], X[pos, 2], marker="o", c='xkcd:sky blue')
# 绘制负样本,使用X形标记,粉红色
plt.scatter(X[neg, 1], X[neg, 2], marker="x", c='xkcd:pink')
# 绘制决策边界
# 生成网格点,范围从-1到1.25,共50个点
u = np.linspace(-1, 1.25, 50)
v = np.linspace(-1, 1.25, 50)
U, V = np.meshgrid(u, v) # 生成50x50的网格点矩阵
# 计算每个网格点的预测值,然后重塑为网格形状
# map_feature将网格点转换为多项式特征,与theta相乘得到预测结果
z = (map_feature(U.flatten(), V.flatten()) @ theta).reshape((50, 50))
# 绘制轮廓线,只显示z=0的线(决策边界,此时预测概率为0.5)
plt.contour(u, v, z, [0], colors='r')
# 设置图表标题、坐标轴标签
plt.title(f"lambda = {lmd}") # 显示当前使用的正则化参数
plt.xlabel('Microchip Test 1') # x轴标签:微芯片测试1
plt.ylabel('Microchip Test 2') # y轴标签:微芯片测试2
# 显示图表
plt.show()
分别绘制出
λ
=
0
,
1
,
5
\lambda = 0,1,5
λ=0,1,5 时的决策边界图如下:

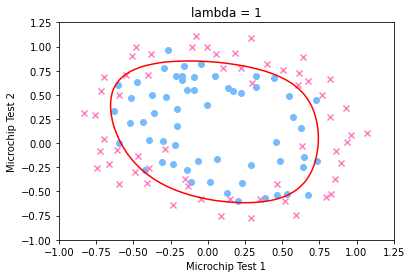
























 282
282

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








