堆排序

概要
堆排序（英语：Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。
图解堆排序过程
1.构建大根堆


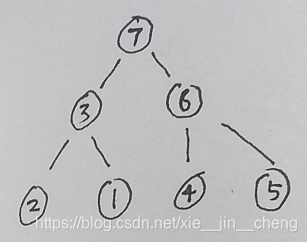
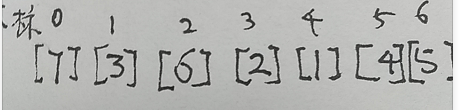
2 排序1


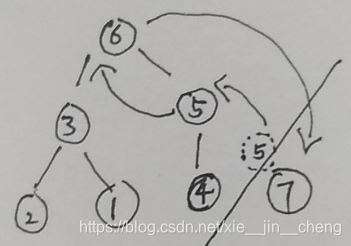
3 排序2


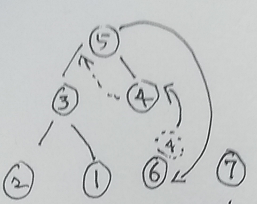
4 排序2~结束：略（重复2的步骤）
我的理解
为什么堆会变快，每放置一个数据只需要遍历二叉树的层，这就是快的关键。
代码

package suanFa;
import  java.util.Arrays;

public class Dui {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int[] array = new int[]{70, 60, 12, 40, 30, 8, 10};
		 
        MaxHeapSort heap = new MaxHeapSort(array);
        System.out.println("================== 执行构建最大堆前堆的结构：==================");
        heap.printHeapTree(heap.heap);
 
        //构造最大堆
        System.out.println("================== 构建最大堆前堆        ：==================");
        heap.BuildMaxHeap();
        System.out.println("================== 执行构建最大堆后堆的结构：==================");
        heap.printHeapTree(heap.heap);
 
        //堆排序
        System.out.println("================== 堆排序               ：==================");
        heap.HeapSort();
        System.out.println("================== 执行堆排序后数组的内容 ：==================");
        heap.printHeap(heap.heap);
 
	}

}
 
class MaxHeapSort {
    int[] heap;
 
    private int heapsize;
 
    public MaxHeapSort(int[] array) {
        this.heap = array;
        this.heapsize = heap.length;
    }
 
    /**
     * 构造最大堆
     */
    public void BuildMaxHeap() {
        for (int i = heapsize / 2; i > 0; i--) {
            System.out.println("------------");
            System.out.println("非子节点位置：" + (i));
            //从最后一个非叶子节点开始，依次向上将当前子树最大堆化
            MaxNode(i);
        }
    }
 
    /**
     * 堆排序
     */
    public void HeapSort() {
        for (int i = 1; i <= heap.length; i++) {
            //执行n次，将每个当前最大的值放到堆末尾
            int tmp = heap[0];
            heap[0] = heap[heapsize - 1];
            heap[heapsize - 1] = tmp;
            heapsize--;
            //从跟节点开始
            MaxNode(1);
        }
    }
    /**
     * 递归exchange 最大值和i位置的值
     *
     * @param i 第几个元素，i-1对应数组heap里的下标，比如根节点为i=1 heap对应的是0
     */
    public void MaxNode(int i) {
        System.out.println("根节点位置：" + i + "，值：" + heap[i - 1]);
        int left = getLeftPosition(i);
        System.out.println("左子节点位置：" + (left));
        int right = getRightPosition(i);
        System.out.println("右子节点位置：" + (right));
        int largest_position;
        if (left <= heapsize && heap[left - 1] > heap[i - 1]) {
            largest_position = left;
        } else {
            largest_position = i;
        }
        if (right <= heapsize && heap[right - 1] > heap[largest_position - 1]) {
            largest_position = right;
        }
        if (largest_position == i || largest_position > heapsize) {//如果largest等于i说明i是最大元素 largest超出heap范围说明不存在比i节点大的子女
            System.out.println(i + "位置，已经不存在比自己值还大的子节点了，最大值就是他自己。。。");
            return;
        } else {
            System.out.println("三个节点中的最大值的位置：" + (largest_position) + ",开始交换位置");
        }
        //交换i与largest对应的元素位置，在largest位置递归调用MaxNode
        exChange(heap, i - 1, largest_position - 1);
 
        System.out.println("-------------");
        MaxNode(largest_position);
    }
 
    /**
     * 获取 i 节点的副节点位置
     *
     * @param i
     * @return
     */
    private int parent(int i) {
        return (i) / 2;
    }
 
    /**
     * 获取 i 节点的左子节点的位置
     *
     * @param i
     * @return
     */
    private int getLeftPosition(int i) {
        return 2 * (i);
    }
 
    /**
     * 获取 i 节点的右子节点的位置
     *
     * @param i
     * @return
     */
    private int getRightPosition(int i) {
        return 2 * (i) + 1;
    }
 
    /**
     * 交换 数组中元素
     *
     * @param arr
     * @param position1
     * @param position2
     */
    private void exChange(int[] arr, int position1, int position2) {
        int temp = arr[position1];
        arr[position1] = arr[position2];
        arr[position2] = temp;
    }
 
    /**
     * 打印 树的结构
     *
     * @param array
     */
    public void printHeapTree(int[] array) {
        int length = array.length;
        for (int i = 1; i < length; i = i * 2) {
            int v = (int) (Math.log(i) / Math.log(2)) + 1;
            for (int k = i - 1; k < 2 * i - 1 && k < length; k++) {
                System.out.print(array[k] + "\t");
            }
            System.out.println();
        }
    }
    public void printHeap(int[] array) {
        System.out.println(Arrays.toString(array));
    }
}

运行结果

================== 执行构建最大堆前堆的结构：==================
70	
60	12	
40	30	8	10	
================== 构建最大堆前堆        ：==================
------------
非子节点位置：3
根节点位置：3，值：12
左子节点位置：6
右子节点位置：7
3位置，已经不存在比自己值还大的子节点了，最大值就是他自己。。。
------------
非子节点位置：2
根节点位置：2，值：60
左子节点位置：4
右子节点位置：5
2位置，已经不存在比自己值还大的子节点了，最大值就是他自己。。。
------------
非子节点位置：1
根节点位置：1，值：70
左子节点位置：2
右子节点位置：3
1位置，已经不存在比自己值还大的子节点了，最大值就是他自己。。。
================== 执行构建最大堆后堆的结构：==================
70	
60	12	
40	30	8	10	
================== 堆排序               ：==================
根节点位置：1，值：10
左子节点位置：2
右子节点位置：3
三个节点中的最大值的位置：2,开始交换位置
-------------
根节点位置：2，值：10
左子节点位置：4
右子节点位置：5
三个节点中的最大值的位置：4,开始交换位置
-------------
根节点位置：4，值：10
左子节点位置：8
右子节点位置：9
4位置，已经不存在比自己值还大的子节点了，最大值就是他自己。。。
根节点位置：1，值：8
左子节点位置：2
右子节点位置：3
三个节点中的最大值的位置：2,开始交换位置
-------------
根节点位置：2，值：8
左子节点位置：4
右子节点位置：5
三个节点中的最大值的位置：5,开始交换位置
-------------
根节点位置：5，值：8
左子节点位置：10
右子节点位置：11
5位置，已经不存在比自己值还大的子节点了，最大值就是他自己。。。
根节点位置：1，值：8
左子节点位置：2
右子节点位置：3
三个节点中的最大值的位置：2,开始交换位置
-------------
根节点位置：2，值：8
左子节点位置：4
右子节点位置：5
三个节点中的最大值的位置：4,开始交换位置
-------------
根节点位置：4，值：8
左子节点位置：8
右子节点位置：9
4位置，已经不存在比自己值还大的子节点了，最大值就是他自己。。。
根节点位置：1，值：8
左子节点位置：2
右子节点位置：3
三个节点中的最大值的位置：3,开始交换位置
-------------
根节点位置：3，值：8
左子节点位置：6
右子节点位置：7
3位置，已经不存在比自己值还大的子节点了，最大值就是他自己。。。
根节点位置：1，值：8
左子节点位置：2
右子节点位置：3
三个节点中的最大值的位置：2,开始交换位置
-------------
根节点位置：2，值：8
左子节点位置：4
右子节点位置：5
2位置，已经不存在比自己值还大的子节点了，最大值就是他自己。。。
根节点位置：1，值：8
左子节点位置：2
右子节点位置：3
1位置，已经不存在比自己值还大的子节点了，最大值就是他自己。。。
根节点位置：1，值：8
左子节点位置：2
右子节点位置：3
1位置，已经不存在比自己值还大的子节点了，最大值就是他自己。。。
================== 执行堆排序后数组的内容 ：==================
[8, 10, 12, 30, 40, 60, 70]