刷题的基础 -- 数据结构之堆

前情提要：

• 堆的相关概念
• 堆的存储方式
• 堆的使用
• 堆实现优先队列
• java中的PriorityQuene实现类以及其模拟

一切的一切开始之前，先了解为什么要学习堆，有什么用，用是最好的学，教是最好的学，往往直接用起来效果会好很多

Dijkstra算法（一种求解最短路径的算法）就是通过最小优先队列来存储结点的集合实现的，这是在图论中的应用场景，好了，虽然但是，我们还暂时无法理解这个算法具体是什么，但是我们可以直到学不好堆就间接学不好一种算法

一、堆的相关概念

1.1 堆是什么？

堆：一个近似完全二叉树的一维数组

注：完全二叉树是一种可以放在顺序表结构中的树结构

堆是一种数据结构；

堆是一种完全二叉树；

堆是一个一维数组；

一图胜千言

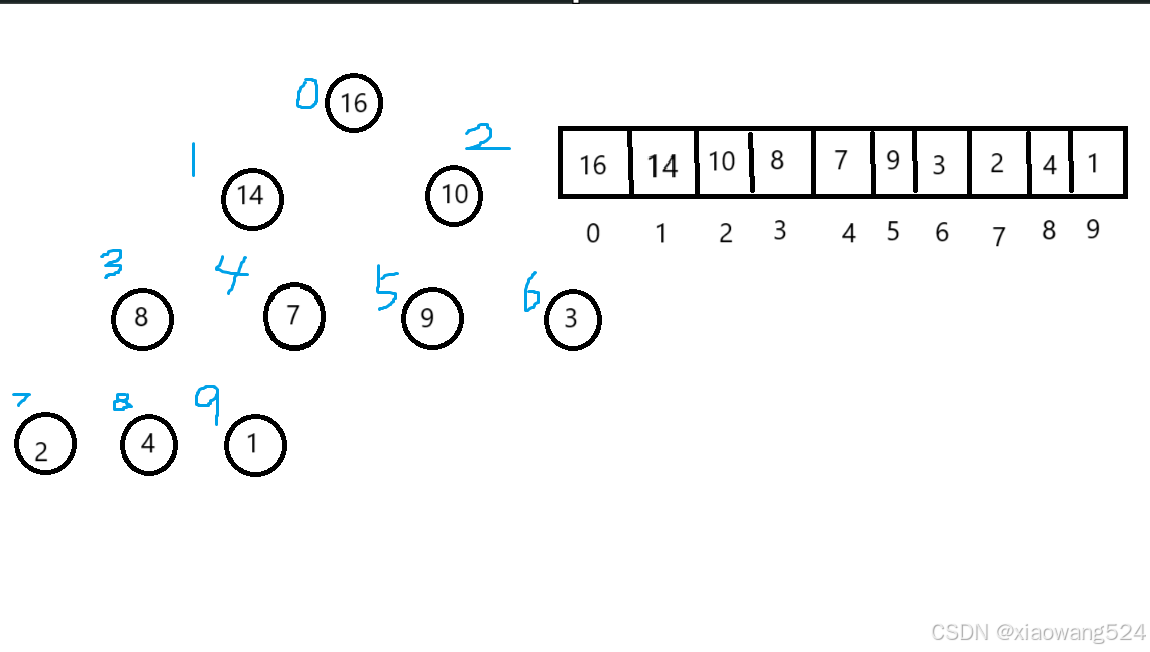
这里就是一个堆的内部结构，数组，但是是一颗完全二叉树

1.2 堆的种类

堆分为最大堆和最小堆

最大堆：所有结点的数值都要比父节点小 -- A[PARENT(i)] >= A[i]，根节点值最大

最小堆：所有结点的数值都要比父节点大 -- A[PARENT(i)] <= A[i]，根节点值最小

图示就是一个最大堆

1.3堆的高度

高度：该节点到叶节点最长简单路径的上边数就是堆的高度

说白了就是该节点到最底层的层数，16这个结点的高度就是4

高度h决定的性质：含n个元素的高度h是(log(n+1)),堆的操作的运行时间与高度成正比，时间复杂度是log(h)

当然还有其他的性质，但是不太理解

满数的结点数n是2^n - 1，层数就是h = 2^n - 1 --> h = log2(n+1);

时间复杂度如图所示：

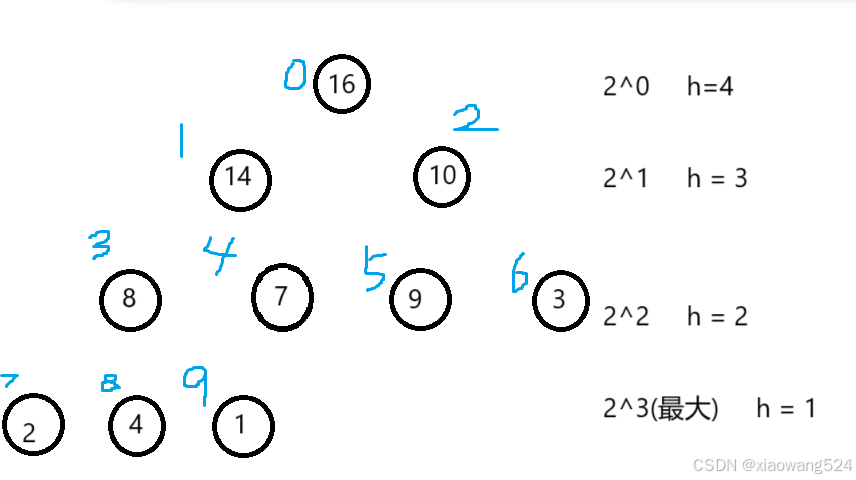
二、堆的使用

着重最大堆的操作，最小堆只要更换大于小于就好了

2.1 维护最大堆 -- MAX-HEAPIFY过程

//以下是伪代码

//树的左子节点
Left(i)
    return 2*i + 1
//树的右子节点
Right(i)
    return 2*i + 2

MAX-HEAPIFY(A,i)
    l = Left(i) //左子节点的值
    r = Right(i) //右字节点的值
    if (A[l] > A[i] && l>0)
        largest = l
    else largest = i
    if(A[r]>A[largest])
        largest = r //以上是为了得到该节点与左子节点右子节点三个节点中的最大值的下标
    if largest != i //如果最大值就是i说明这个小部分就是最大堆，不用改变；如果不是i，就要将最大值的值与根结点的值进行交换，达到最大堆的定义
    exchange A[i] with A[largest]
    MAX-HEAPIFY(A,largest)//这一行代码的意思是，就算交换之后的数字也可能不能满足最大值的定义，因此需要将这个小部分再次进行判断，但是接下来也可能右想通过的情况，因此需要使用递归不断形成接下来的最大堆，递归可能不太好理解，只要在意一个递归的一个部分就好了，相信递归函数会帮你完成他的使命，注意这时的最大值是原来那个小部分的i，而不是最大值的意思

//这是维护最大堆过程的一个方法，也是一种向下比较

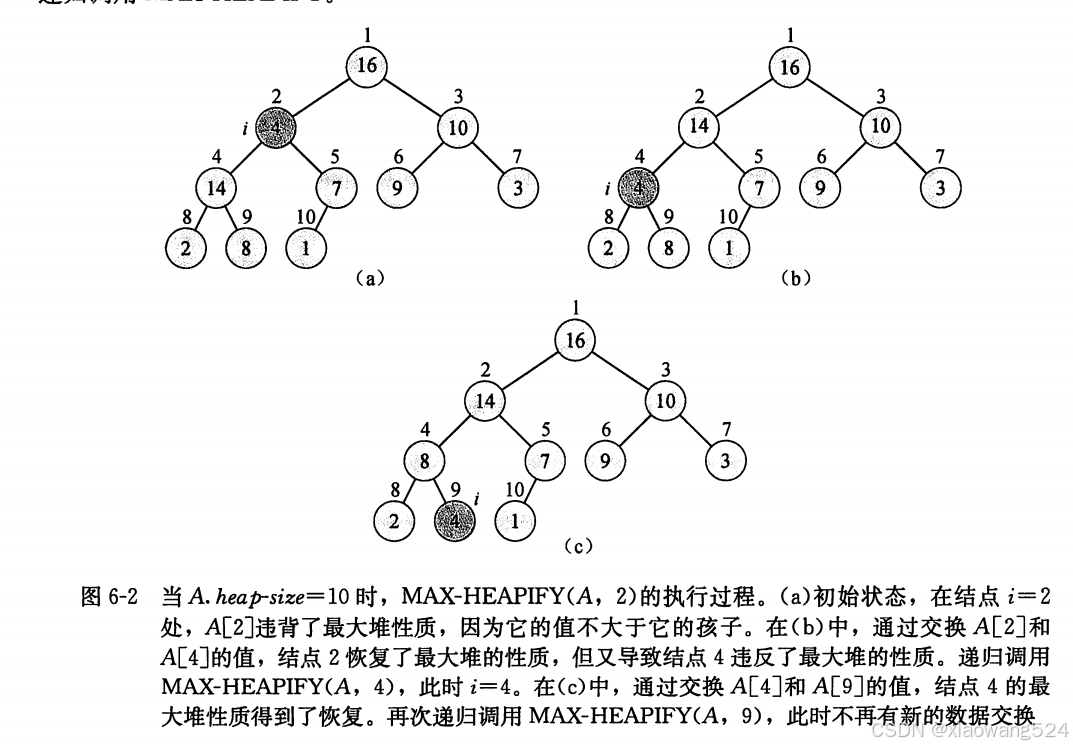
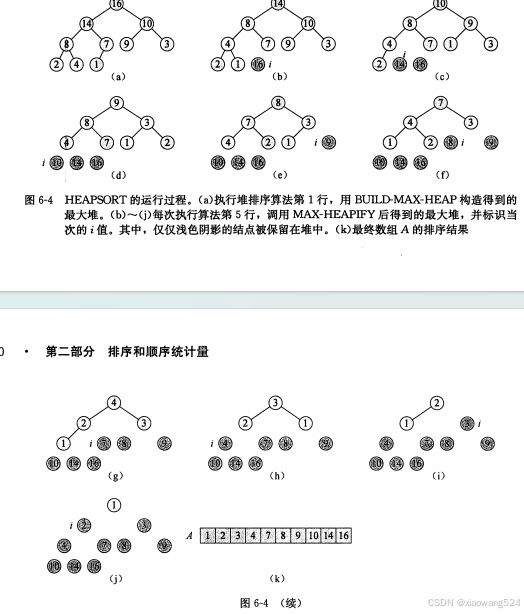
这里引用《算法导论》一书中的图便于理解，当然也可以去看看这本书

2.2 从无序数组中构造最大堆

核心：从最后一个非叶子结点的根节点开始构造最大堆

为什么不从第一个结点开始，因为这里并不是完全符合定义的完全二叉树，并不会得到层序遍历结果是依次增大的结果，而再次往下会出现已经形成最大堆，给到下一个的时候同样形成最大堆，可是这里二次得到的最大堆可能比一次最大值还要大，这就要回去遍历，为了避免这种尴尬情况就要开始就从下往上遍历

BUILD(A)
    A.heap-size = A.length //得到堆的长度，并不是数组中所有的元素都要放到堆中
    for i = (length-2)/2 downto 0 // downto 的意思是i--
//这里的重点是(length - 2)/2以及i--，length-1是最后一个结点的下标，但是是叶节点，不是我们想要的最后一个堆结点，因此根据完全二叉树的性质可以得到，最后一个叶节点的父节点就是最后一个根节点，而得到父节点的下标就是 (i-1)/2，这里是数组下标为0开始，所以左子节点和右子节点最后的结果都能找到父节点
        MAX-HEAPIFY（A,i）//核心一直都是维护最大堆，每一次都要维护一次，但是这样递归的次数就变得非常多，明显可以优化，后面将会介绍java中的向上遍历简化这里的递归

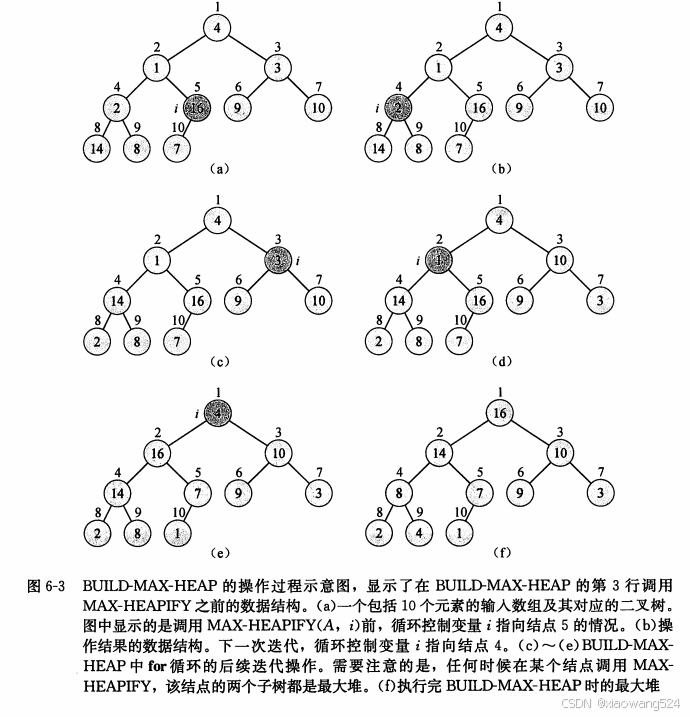
时间复杂度:o(n) 利用等比数列推导可得

2.3 堆排序

HEAPSORT(A)
    BUILD(A)
    for i = A.length downto 1
    exchange A[0] with A[i]
    MAX-HEAPIFY(A,i)
//排序的基本思路：
//先构造最大堆
//将子节点一一移除堆(剪叶子)：a.交换根节点和叶节点 b. 剪叶 c.维护最大堆
//最后得到的就是顺序排列的数组，这里是将根结点一点点变小

2.4 利用堆实现优先队列

优先队列：一种用来维护一组元素组成的集合S的数据结构，其中每一个元素都有对应的关键字，同时也有确定对象的句柄

也分为最大优先队列和最小优先队列

方法分别是：

MAXIMUM(S) 返回最大值 //MINMUM

MAX(A)
    return A[0]

INSERT(S,x) 在S中插入x

INCREASE(A,x)
    A.heap-size = A.heap-size +1//为x开辟一块新的空间并且放进去
    A[A.heap-size ] = -1 
    INCREASE(A,A.heap-size,x)//巧妙利用INCREASE插入元素

EXTRACT-MAX（S）返回并移除最大值 //MIN

EXTRACT - MAX(A)
    if(A.heap-size<1)
        error "nomax"
    max = A[0] //记录返回的最大值
    A[0] = A[heap-size-1] //将最后一个下标的值变成根
    A.heap - size = A.heap - size - 1 //少了一个值，数组长度减小
    MAX-HEAPIFY(A,0) //维护
    return max

INCREASE(S,x,k) 将x位置的值增加到K //DECREASE

INCREASE(A,i,key)
    if key < A[i]
        error
    A[i] = key
    while i>1 and A[i] > A[PARENT(i)]
        A[PARENT(i)] = A[i]
        i = PARENT(i) //将key赋值之后一步步向上构造最大堆

三、JAVA实现优先队列

public class MyPriorityQueue {
    public int[] elem;
    public int usedSize;

    public PriorityQueue() {
        this.elem = new int[11];
    }

    /**
     * 建堆的时间复杂度：
     *
     * @param array
     */
    public void createHeap(int[] array) {
        if(elem.length>array.length)
        {
            for(int i =0;i<array.length;i++){
                elem[i] = array[i];
                usedSize++;
            }
            for(int j = (usedSize-2)/2;j>=0;j--){
                shiftDown(j,usedSize);
            }
        }
        else{
            elem = Arrays.copyOf(elem,2*elem.length);
        }
    }

    /**
     *
     * @param root 是每棵子树的根节点的下标
     * @param len  是每棵子树调整结束的结束条件
     * 向下调整的时间复杂度：O(logn)
     */
    private void shiftDown(int root,int len) {
        //先找出左右孩子下标最大值
        int child = 2*root +1;
        while(child<usedSize){
            if(elem[child] < elem[child + 1] && child + 1<usedSize){
                child++;
            }
            if(elem[child] > elem[root]){
                swap(root,child);
                root = child;
                child = child*2+1;
            }
            else{
                break;
            }
        }
    }

    public void swap(int p,int c){
        int tmp = elem[p];
        elem[p] = elem[c];
        elem[c] = tmp;
    }

       */
    public void push(int val) {
        usedSize = usedSize -1;
        elem[usedSize] = val;
        shiftUp(usedSize);
    }

    private void shiftUp(int child) {
        int p = (child -1)/2;

        while( child >1 && elem[child] > elem[p]){
            swap(p,child);
            child = p;
            p = (child -1)/2;
        }
    }

    public boolean isFull() {
        return usedSize == elem.length;
    }

    /**
     * 出队【删除】：每次删除的都是优先级高的元素
     * 仍然要保持是大根堆
     */
    public void pollHeap() {
        int max = elem[0];
        swap(0,usedSize -1);
        usedSize--;
        shiftDown(0,usedSize);

        return max;
    }

    public boolean isEmpty() {
        return usedSize == 0;
    }

    /**
     * 获取堆顶元素
     * @return
     */
    public int peekHeap() {
        return elem[0];
    }

    public int heapSort(){
        int end = usedSize-1;
        while(end>0){
            swap(0,end);
            shiftDown(0,end);
            end--;
        }
    }
}