【数据结构】顺序线性表-优快云博客

在数据结构的宏大版图中，线性表堪称基石般的存在，是我们开启数据结构探索之旅的重要起点。它就像是一个井然有序的队列，每个元素都有其特定的位置和顺序，这种有序性使得数据的组织和管理变得高效而便捷。无论是简单的数据存储，还是复杂算法的构建，线性表都扮演着不可或缺的角色，为解决各种实际问题提供了强大的支持。

而线性表的顺序表示，作为线性表的一种重要存储方式，更是以其独特的优势和特点，在数据处理领域占据着重要的地位。它将线性表中的元素按照顺序依次存储在连续的内存空间中，就像把一排物品整齐地摆放在书架上，每个物品都紧密相邻，这种存储方式不仅直观易懂，而且为快速访问和操作数据提供了可能。接下来，就让我们一起深入探寻线性表顺序表示的奥秘，揭开它神秘的面纱。

二、揭开顺序表示的神秘面纱

（一）顺序表示的定义与原理

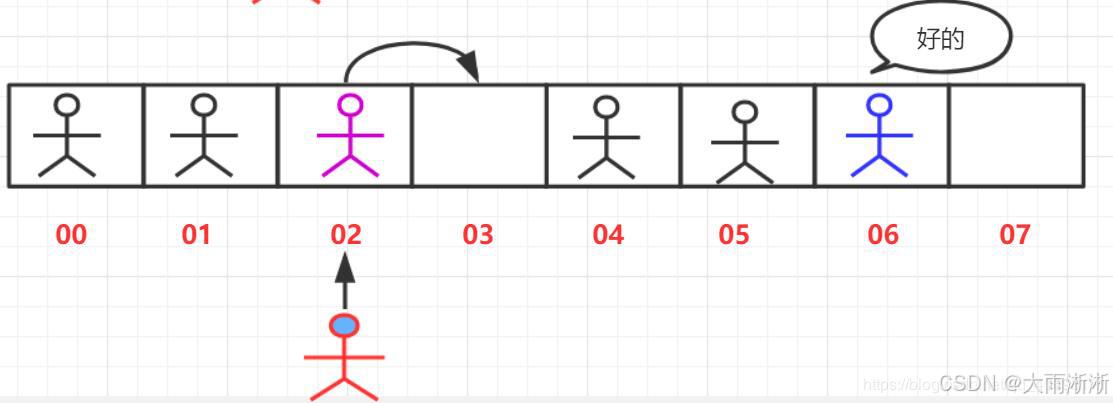
线性表的顺序表示，简单来说，就是用一组地址连续的存储单元依次存储线性表中的数据元素。就好比我们有一排连续的信箱，每个信箱都有自己的编号，从 1 号信箱开始，依次往后排列。我们把数据元素看作是信件，按照顺序依次放入这些信箱中，这样就形成了线性表的顺序存储结构。

在这种存储方式中，每个数据元素都有其对应的存储位置，而且这些位置是连续的。假设我们有一个线性表，每个元素占用\(l\)个存储单元，并且以所占的第一个单元的存储地址作为数据元素的存储位置。那么，线性表中第\(i+1\)个数据元素的存储位置\(LOC(a_{i+1})\)和第\(i\)个数据元素的存储位置\(LOC(a_i)\)之间满足这样的关系：\(LOC(a_{i+1}) = LOC(a_i) + l\) 。这意味着，只要我们知道了第一个数据元素的存储地址（也就是基地址），就可以通过这个公式计算出其他任意一个数据元素的存储地址，从而实现对线性表中数据元素的随机存取。

（二）顺序表与数组的 “亲密关系”

在实际应用中，线性表的顺序表示通常借助数组来实现。这是因为高级程序设计语言中的数组类型具有随机存取的特性，正好与线性表顺序存储的需求相契合。数组中的元素在内存中也是连续存储的，我们可以通过数组的下标快速地访问到数组中的任意一个元素，这与线性表通过位序访问元素的方式非常相似。

不过，需要注意的是，顺序表中的位序和数组的下标虽然都用于定位元素，但它们之间还是存在一些细微的差别。顺序表中的位序是从 1 开始计数的，而数组的下标通常是从 0 开始计数的。例如，在一个顺序表中，第一个元素的位序是 1，而在对应的数组中，第一个元素的下标是 0。在进行编程实现时，我们必须要清楚地认识到这一点，避免因为混淆而导致错误。

二、顺序表的 “生存法则”：基本操作

（一）初始化：搭建顺序表的 “基石”

初始化是顺序表的 “诞生仪式”，它为顺序表的后续操作奠定了基础。在初始化顺序表时，我们需要为其分配一块连续的内存空间，就像为一座房子划定建造的土地。这块内存空间的大小通常是根据顺序表可能存储的最大元素数量来确定的，也就是顺序表的容量。

以 C 语言为例，我们可以使用malloc函数来分配内存空间。假设我们要创建一个存储整数类型元素的顺序表，并且初始容量为 100，代码如下：

#define MAX_SIZE 100

typedef struct {

int *data; // 存储数据的数组

int length; // 当前顺序表的长度

} SeqList;

void InitList(SeqList *L) {

L->data = (int *)malloc(MAX_SIZE * sizeof(int));

if (L->data == NULL) {

// 内存分配失败的处理

printf("内存分配失败\n");

exit(1);

}

L->length = 0; // 初始长度为0

}

在这段代码中，malloc(MAX_SIZE * sizeof(int))语句为顺序表分配了可以存储 100 个整数的内存空间，并将这块空间的首地址赋值给data指针。同时，将顺序表的长度初始化为 0，表示此时顺序表中还没有存储任何元素。通过这样的初始化操作，我们就搭建好了顺序表的 “基石”，为后续的数据存储和操作做好了准备。

（二）插入操作：元素的 “插队” 之旅

插入操作是向顺序表中添加新元素的过程，就像是在排队时有人想要 “插队” 一样。在顺序表中插入元素时，我们需要指定插入的位置和要插入的元素值。不过，这个过程并非一帆风顺，需要进行一系列的判断和操作。

首先，我们要检查插入位置的合法性。插入位置必须在 1 到顺序表当前长度加 1 之间，否则就会出现越界错误。例如，如果顺序表的长度为 5，那么合法的插入位置就是 1、2、3、4、5、6。如果插入位置小于 1 或者大于顺序表长度加 1，就需要提示用户插入位置不合法。

接下来，我们要考虑顺序表的容量问题。如果顺序表当前的元素数量已经达到了其最大容量，那么就需要进行扩容操作，为新元素腾出空间。扩容的方式有很多种，常见的是重新分配一块更大的内存空间，将原顺序表中的元素复制到新空间中，然后释放原空间。

假设我们要在顺序表L的第i个位置插入元素x，具体的操作步骤如下：

检查插入位置i是否合法，如果不合法则返回错误。
检查顺序表是否已满，如果已满则进行扩容。
将从第length到第i个位置的元素依次向后移动一位，为新元素腾出位置。
将新元素x插入到第i个位置。
顺序表的长度length加 1。

下面是用 C 语言实现的插入操作代码：

bool ListInsert(SeqList *L, int i, int x) {

if (i < 1 || i > L->length + 1) {

printf("插入位置不合法\n");

return false;

}

if (L->length == MAX_SIZE) {

// 进行扩容操作

int *newData = (int *)malloc(2 * MAX_SIZE * sizeof(int));

if (newData == NULL) {

printf("内存分配失败\n");

return false;

}

for (int j = 0; j < L->length; j++) {

newData[j] = L->data[j];

}

free(L->data);

L->data = newData;

MAX_SIZE *= 2;

}

for (int j = L->length; j >= i; j--) {

L->data[j] = L->data[j - 1];

}

L->data[i - 1] = x;

L->length++;

return true;

}

插入操作的时间复杂度主