【数据结构】AVL树的搭建及插入结点

一、实例

我们通过一个实例来说明整个结点的插入导致失衡的过程

（1）AVL初始状态

（2）不失平衡的插入

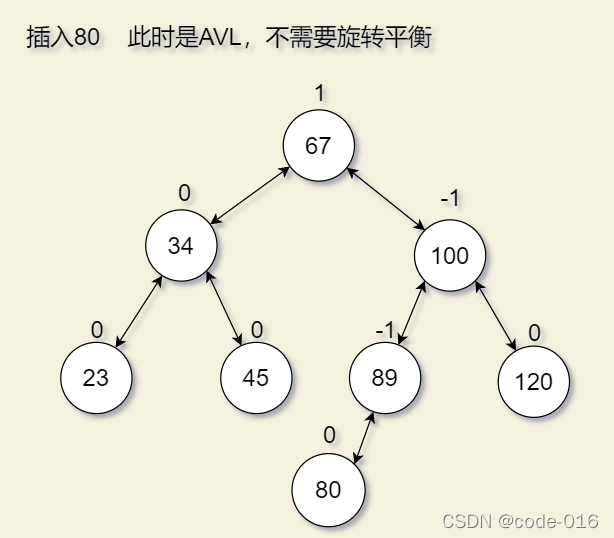
（3）失去平衡的插入

我们在(2)的基础上增加了以下两种情况

注意： 上图的结点的平衡因素只设置了一部分

二、构建过程分析

（1）大体流程

（2）具体函数功能

1. insert

该函数的主要功能就是根据二叉搜索树的insert函数增加了个PassBalance函数进行结点的平衡

//插入函数
bool insert(AVLTree& tree, ElemType val)
{
	if (tree == nullptr)
	{
		tree = BuyNode(val);
		return true;
	}
	AVLNode* pa = nullptr;
	AVLNode* ptr = tree;
	while (ptr != nullptr && ptr->key != val)
	{
		pa = ptr;
		ptr = val < ptr->key ? ptr->leftchild : ptr->rightchild;
	}
	//说明是因存在而退出循环
	if (ptr != nullptr && ptr->key == val)
	{
		return false;
	}
	//申请结点
	ptr = BuyNode(val);
	ptr->parent = pa;
	if (ptr->key < pa->key)
	{
		pa->leftchild = ptr;
	}
	else
	{
		pa->rightchild = ptr;
	}
	//插入结点后，进入平衡调整
	PassBalance(tree, ptr);
	return true;
}

2. PassBalance函数

//平衡回溯直接修改平衡因子
void PassBalance(AVLTree& tree, AVLNode* ptr)
{
	AVLNode* pa = ptr->parent;
	bool tag = true;
	while (pa != nullptr && tag)
	{
		//左边插入的结点
		if (ptr == pa->leftchild)
		{
			//修改左边的平衡因子
			switch (pa->balance)
			{
			case 0: pa->balance = -1; break;
			case 1: 
				pa->balance = 0; 
				tag = false;
				break;
			case -1: 
				//pa->balance = -2;
				//进行左平衡
				LeftBalance(tree, pa); //pa是第一层结点
				tag = false;
				break;
			}
		}
		//右边插入的结点
		else 
		{
			//修改右边的平衡因子
			switch (pa->balance)
			{
			case 0: pa->balance = 1; break;
			case 1: 			
				//pa->balance = 2;
				//进行右平衡
				RightBalance(tree, pa);
				tag = false;
				break;
			case -1: 
				pa->balance = 0; 
				tag = false;
				break;
			}
		}
		ptr = pa;
		pa = pa->parent;
	}
}

3. LeftBalance函数

//平衡左子树
void LeftBalance(AVLTree& tree, AVLNode* ptr)
{
	AVLNode* leftsub = ptr->leftchild;
	AVLNode* rightsub = nullptr;

	switch (leftsub->balance)
	{
	case -1: 
		//直线状：单右旋
		ptr->balance = 0;
		leftsub->balance = 0;
		RotateRight(tree, ptr);
		break;
	case 1:
		//折线状：双旋转
		rightsub = leftsub->rightchild;
		switch (rightsub->balance)
		{
		case -1:
			leftsub->balance = 0;
			ptr->balance = 1;
			break;
		case 1:
			leftsub->balance = -1;
			ptr->balance = 0;
			break;
		case 0:
			leftsub->balance = 0;
			ptr->balance = 0;
			break;
		}
		rightsub->balance = 0;
		RotateLeft(tree, leftsub);
		RotateRight(tree, ptr);
		break;
	}
}

4. RightBalance函数

//平衡右子树
void RightBalance(AVLTree& tree, AVLNode* ptr)
{
	AVLNode* rightsub = ptr->rightchild;
	AVLNode* leftsub = nullptr;
	switch (rightsub->balance)
	{
	//直线
	case 1:
		rightsub->balance = 0;
		ptr->balance = 0;
		RotateLeft(tree, ptr);
		break;
	//折线:双旋转
	case -1:
		leftsub = rightsub->leftchild;
		//修改双旋因子
		switch (leftsub->balance)
		{
		case 0:
			rightsub->balance = 0;
			ptr->balance = 0;
			break;
		case 1:
			rightsub->balance = 0;
			ptr->balance = -1;
			break;
		case -1:
			rightsub->balance = 1;
			ptr->balance = 0;
			break;
		}
		leftsub->balance = 0;
		RotateRight(tree, rightsub);
		RotateLeft(tree, ptr);
		break;
	}
}

三、测试

int main()
{
	int arr[] = {16,3,7,11,9,26,18,14,15};
	AVLTree tree = nullptr;
	for (auto& x : arr)
	{
		insert(tree, x);
	}
	Order(tree);
	Clear(tree);
	return 0;
}