本文介绍使用BFS算法求解包含多个钥匙位置的地图中，从起点到终点的最短路径问题。通过增加状态维度优化搜索过程，避免多次BFS造成的效率低下。
对此题有疑问的小伙伴们，相信你们之前肯定对BFS广度优先搜索算法有所了解，也做过一些较为基础的例题，最经典的问题之一应该是迷宫问题，从起点S出发，求到达终点E的最短路径，迷宫问题的解决思路是利用BFS从起点S出发，一层一层往外进行地毯式的搜索，直至到达终点E，即可求出最短路径。可以看出，在迷宫问题中，我们只需要应用一次BFS算法，即可求出最短路径。因为起点S和终点E的坐标都只有一个，即有唯一的起点坐标和终点坐标。
解题思路：
首先来分析一下问题， 这道题最关键的一个地方就是钥匙被放置在多处，蒜头君有多种选择，那怎么知道哪一条路径(起点->钥匙位置->家)是最短的呢？
在这里，我就以一个简单地图的例子来说明，为大家讲清楚这个问题 如下图，是一个4行6列的地图，S为起点，T为终点，P为钥匙，#为障碍物，不可通行
分析：从以上地图分析出，要从起点S开始走，然后拿到钥匙P，最后到达终点T，有两条最短路径可以走，这两条路径分别是：
路径一：总共需要9步
路径二：总共需要7步
算出以上两条路径之后，我们还需要取其中最短的一条路径，即5+2=7。所以蒜头君拿钥匙 回家的最短路径是7。
再次分析：以上地图中有两把钥匙，所以我们需要分别求出经过这两把钥匙再回到家的最短路径，即求出每把钥匙到家到起点的这两个值，然后将其相加，求出某条最短路径。然后将n条回家的路径进行比较，算出蒜头君回家的最短路径。也就是说当算一把钥匙到家和到起点的最短距离时，我们需要应用两次BFS，如果说地图中有非常多把钥匙，那么要进行的BFS次数就非常多了，此时程序会超时。那有没有别的方法可以解决程序超时的问题呢？或者说这道题要怎么优化？
优化的思路：我们可以在BFS的时候将标记数组多开一维度，表示是否已经取得了钥匙的状态。如果到达终点并且取得钥匙的状态被标记，bfs结束，即找到了最短路径。可能你还是无法理解，我们不妨用刚刚那个例子来进行一个讲解，首先，我们有一个4行6列的地图，S为起点，T为终点，.为道路(钥匙和家所在的地方也可以视为道路)，#为障碍物，不可通行，如下图所示：
我们来模拟一下BFS的执行过程，大家都知道BFS的执行需要队列和标记数组。为了表示每一个坐标的状态(走到当前坐标时手上是否有钥匙、当前坐标的位置、走到当前坐标时距离起点S经过了多少步)，我们需要构建一个结构体struct，结构体的成员包括如下几个：
注意：此处为也可以不为结构体添加构造函数，添加构造函数的目的时方便我们构造结构体变量，不要也行，只不过，构造结构体变量时，就显得复杂一点而已。
模拟步骤：
第一步：起点S在(4,2)处，将其入队，此时队列里有一个元素，并且设置为起点访问过，此时蒜头君身上没有钥匙，此坐标点所表示的队列元素的值为：
第二步：将S点周围的点全部入队，我们不妨约定，按照右 下 左 上的方向进行BFS,要注意看图示内容的文字说明，后面的步骤大同小异
第三步：S点扩展完毕，出队，请注意看图示文字说明
第四步：扩展(4,3)点，如下图所示：
第五步：(4,3)出队，此时队首元素是(3,2)，从(3,2)开始扩展
以上第9行第3列写错了，2代表的含义应该是距离S共2步
第六步：扩展(3,2)点，如下图所示：
第七步：(3,2)扩展完毕，出队，如下图所示：
第八步：扩展(3,3)点，如下图所示：
第九步：(3,3)扩展完毕，出队，如下图所示：
第十步：(3,1)是队首元素，开始扩展，如下图所示：
第11步：(3,1)出队，如下图所示
第12步：(2,2)是队首元素，开始扩展，如下图所示：
第13步：(2,2)出队，如下图所示
第14步：(3,4)是队首元素，开始扩展，如下图所示：
第15步：(3,4)出队，如下图所示
第16步：(2,1)是队首元素，开始扩展，如下图所示：
第17步：(2,1)出队，如下图所示
第18步：(1,2)是队首元素，开始扩展，如下图所示：
第19步：(1,2)出队，如下图所示
第20步：(3,5)是队首元素，开始扩展，如下图所示：
第21步：(3,5)出队，如下图所示
第21步：(2,4)为队首元素，开始扩展，发现它不能扩展任何点，出队
第22步：(1,1)为队首元素，开始扩展，注意：从(1,1)这个点开始，蒜头君已经获得了钥匙，所以此时v[x][y][1]这个元素派上用场了，观察图示，你会发现之前用的都是v[x][y][0]
第23步：(1,1)出队，如下图所示
第23步：(1,3)为队首元素，开始扩展，没有点可扩展，(1,3)出队，如下图所示
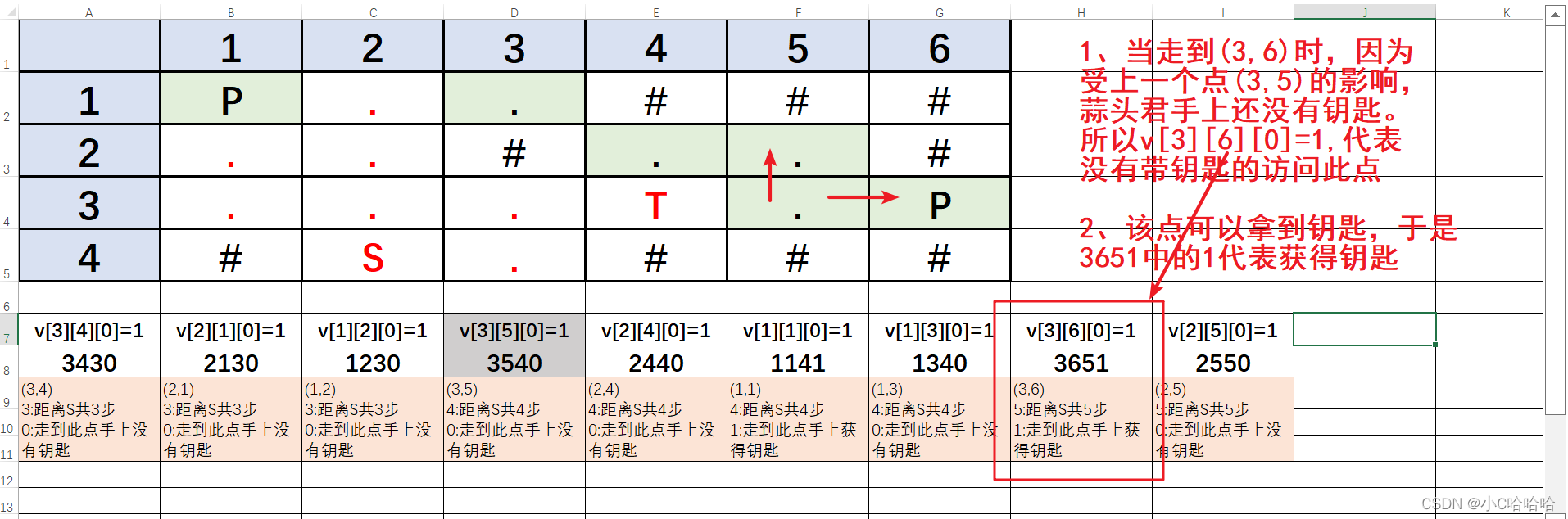
第24步：(3,6)为队首元素，开始扩展
第25步：(3,6)出队，如下图所示
第26步：(2,5)为队首元素，开始扩展，没有元素可扩展，(2,5)出队，如下图所示
第27步：(1,2)为队首元素，开始扩展
第28步：(1,2)出队，如图所示：
第29步：(2,1)为队首元素，开始扩展
第30步：(2,1)出队，如图所示：
第31步：(3,5)为队首元素，开始扩展，发现，当扩展到该点左边的点的时候，到达终点，可以直接得出最短路径为7
分析总结：我们发现，整个过程只用了1次BFS，便求出了蒜头君拿到钥匙然后回家的最短路径，因为我们引入了一个关键的数据结构—为标记数组多开了一个维度，v[x][y][0]代表没有钥匙时是否访问了v[x][y][0]=0代表(x,y)点在没有钥匙时，也没有被访问，v[x][y][0]=1代表在没有钥匙时，该点被访问，v[x][y][1]=0代表(x,y)点在有钥匙时，没有被访问，v[x][y][1]=1，代表有钥匙，该点被访问。这一段话要仔细去斟酌。
代码实现1：
#include<bits/stdc++.h> using namespace std; /* 算出拿钥匙的路+回家的路的最短距离 思路1：求出钥匙到家到起点的两个值，将二者相加即可，求出最小的即为 最短距离 思路2：较难理解，可以利用excel表格画图 提示：同学们要注意，老师上课讲得一些题目都非常经典，那么都是取自于历年的一些真题，上课以题目为主 通过题目的方式去讲解相关的知识，所以同学们一定要学会相关的一些写法以及相关的一些思路 样例1： 8 10 P.####.#P# ..#..#...# ..#T##.#.# .......... ..##.##### .......... #####...## ###....S## 样例1答案： 21 */ const int N = 2005; int n,m; //地图大小 int sx,sy,ex,ey; //起点和终点 int dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}}; //右 下 左 上 char a[N][N]; //地图是一个二维数组，行列不超过2000 bool v[N][N][2]; //一般搜索都会涉及到一个访问数组，不管是DFS还是BFS，都需要将访问过的点设置为已经访问 // 要特别注意v这个数组的含义，第三维用来标记蒜头君走过某个点的时候是否已经带了钥匙 struct node { int x,y; //坐标 int step; bool flag; //钥匙的状态，1代表有钥匙，0代表没有钥匙 //为了更好进行入队，添加构造函数 node(int xx,int yy,int stepp,bool flagg) { x=xx; y=yy; step=stepp; flag=flagg; } }; queue<node> q; int bfs(int x,int y) { //一开始在起点时步数为0，并且手里没有钥匙,可以用false代表，也可以用0代表 q.push(node(x,y,0,false)); v[x][y][0]=true; //第三维为0，因为时没有钥匙的状态，true代表访问，也可以用1代表 while(!q.empty()) { //获取队首元素 node now = q.front(); q.pop(); //获取队首元素之后，就可以实现出队了，因为队首元素已经保存在now了，不会丢失 //队首可扩展的点进行入队 for(int i=0;i<4;i++) { int tx=now.x+dir[i][0]; int ty=now.y+dir[i][1]; if(tx>=0&&tx<n&&ty>=0&&ty<m&&a[tx][ty]!='#'&&!v[tx][ty][now.flag]) { v[tx][ty][now.flag]=1; if(a[tx][ty]=='P') { q.push(node(tx,ty,now.step+1,true)); } else if(a[tx][ty]=='T'&&now.flag==1) { return now.step+1; } else { q.push(node(tx,ty,now.step+1,now.flag)); //此点是否带了钥匙受队首元素的影响 } } } } } int main() { cin>>n>>m; //n行m列 for(int i=0;i<n;i++) { cin>>a[i]; } //寻找起点S的坐标位置 for(int i=0;i<n;i++) { for(int j=0;j<n;j++) { if(a[i][j]=='S') { sx=i; sy=j; } } } //从起点出发，进行bfs cout<<bfs(sx,sy); return 0; }代码实现2：
#include<bits/stdc++.h> using namespace std; /* 算出拿钥匙的路+回家的路的最短距离 思路1：求出钥匙到家到起点的两个值，将二者相加即可，求出最小的即为 最短距离 思路2：较难理解，可以利用excel表格画图 提示：同学们要注意，老师上课讲得一些题目都非常经典，那么都是取自于历年的一些真题，上课以题目为主 通过题目的方式去讲解相关的知识，所以同学们一定要学会相关的一些写法以及相关的一些思路 样例1： 8 10 P.####.#P# ..#..#...# ..#T##.#.# .......... ..##.##### .......... #####...## ###....S## 样例1答案： 21 */ const int N = 2005; int n,m; //地图大小 int sx,sy,ex,ey; //起点和终点 int dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}}; //右 下 左 上 char a[N][N]; //地图是一个二维数组，行列不超过2000 bool v[N][N][2]; //一般搜索都会涉及到一个访问数组，不管是DFS还是BFS，都需要将访问过的点设置为已经访问 // 要特别注意v这个数组的含义，第三维用来标记蒜头君走过某个点的时候是否已经带了钥匙 struct node { int x,y; //坐标 int step; bool flag; //钥匙的状态，1代表有钥匙，0代表没有钥匙 //为了更好进行入队，添加构造函数 node(int xx,int yy,int stepp,bool flagg) { x=xx; y=yy; step=stepp; flag=flagg; } }; queue<node> q; void bfs(int x,int y) { //一开始在起点时步数为0，并且手里没有钥匙,可以用false代表，也可以用0代表 q.push(node(x,y,0,false)); v[x][y][0]=true; //第三维为0，因为时没有钥匙的状态，true代表访问，也可以用1代表 while(!q.empty()) { //获取队首元素 node now = q.front(); q.pop(); //获取队首元素之后，就可以实现出队了，因为队首元素已经保存在now了，不会丢失 //判定是否抵达终点 if(a[now.x][now.y]=='T') { if(now.flag) { cout<<now.step<<endl; break; } continue; //到达终点但是没有钥匙，这个点无需再扩展 } //队首可扩展的点进行入队 for(int i=0;i<4;i++) { int tx=now.x+dir[i][0]; int ty=now.y+dir[i][1]; if(tx>=0&&tx<n&&ty>=0&&ty<m&&a[tx][ty]!='#'&&!v[tx][ty][now.flag]) { v[tx][ty][now.flag]=1; if(a[tx][ty]=='P') { q.push(node(tx,ty,now.step+1,true)); } else { q.push(node(tx,ty,now.step+1,now.flag)); //此点是否带了钥匙受队首元素的影响 } } } } } int main() { cin>>n>>m; //n行m列 for(int i=0;i<n;i++) { cin>>a[i]; } //寻找起点S的坐标位置 for(int i=0;i<n;i++) { for(int j=0;j<n;j++) { if(a[i][j]=='S') { sx=i; sy=j; } } } //从起点出发，进行bfs bfs(sx,sy); return 0; }
总结： 如果对以上的讲解内容或者代码有任何疑问的话，可在评论区里回复，我会及时答复，也可以私信我，将你添加到算法群聊中，一起来学习成长。这一期的算法课堂到这里就结束啦！
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
