数据结构算法-动态规划算法

引言

在遥远的偏东方大陆，名叫坤坤有一位国王，突然有一位杀戮的神明叫弟理，他和他的七位神明 分别为风岩雷草水火冰七位 设杀他和他的子民 有些高科技的东西也设置为攻击性了，后来其中一位名为小坤坤 带着失去的记忆踏上了寻找着当年的记忆，也许名为坤坤的国王并没有在这场战争中逝去，而是失去记忆，把自己藏在蛋中 就像仙侠重生一样，当然这是后话了 只要找到神秘的弟理就能恢复记忆，当然在这之前制作小机器人代我寻找 七国顺便帮我恢复记忆！机器人会知道七国 名叫小可爱， 当然我坐着看他如何做并且不需要指导，他开始学会走台阶当然他走台阶是倒着走，逆天！，当然这没什么 他知道他之前国家可是什么样的机器人都有 ，甚至包括…

他怎么走，他该怎么做 我制定了一些秩序，他可以走一步，也可以走两步 问题来啦，走第n步总共有多少种走法
突然愣住了添加走台阶功能怎么写呢
突然坤坤跨过次元界找到了一位没啥知名度的名叫小森 的来写 ，写这种？分而治之？可以吧
也行吧
一会儿的时间就写完了

int TakeSteps_divide(int n) {

	if (n<=0){
		return 0;
	}

	int ret;
	switch (n){

	case 1:
		ret = 1;
		break;
		
	case 2:
		ret = 2;
		break;

	default:
		ret = TakeSteps_divide(n - 2) + TakeSteps_divide(n - 1);
		break;
	}

	return ret;
}
int main(void) {

	int n;

	cout << "请输入台阶的数目：";
	cin >> n;

	cout << "一共有" << TakeSteps_divide(n) << "走法" << endl;



	return 0;
}

首先扫描有多少个台阶 小森好奇地问道：他怎么扫描难道感知能力超越了一切？ 逆天！坤：也没啥后面有一颗感知一切万物的芯片，核弹GTX980，（？ 什么英伟达？难道你跨次元也跨得太早些吧 现在算力芯片，我不能说，我不能说，）小森的独白 ，好！ 憋住！ 你说：GTX980？ emmm纳这个当算力芯片，不会有逝吧， “不会“坤坤 咱们继续！ 正在扫描！获取台阶是10个
计算能走的台阶有… emmm看来是碰到了递归瓶颈 ！ 跟你说一下：
比如说 有6个台阶
那么如图所示 ：

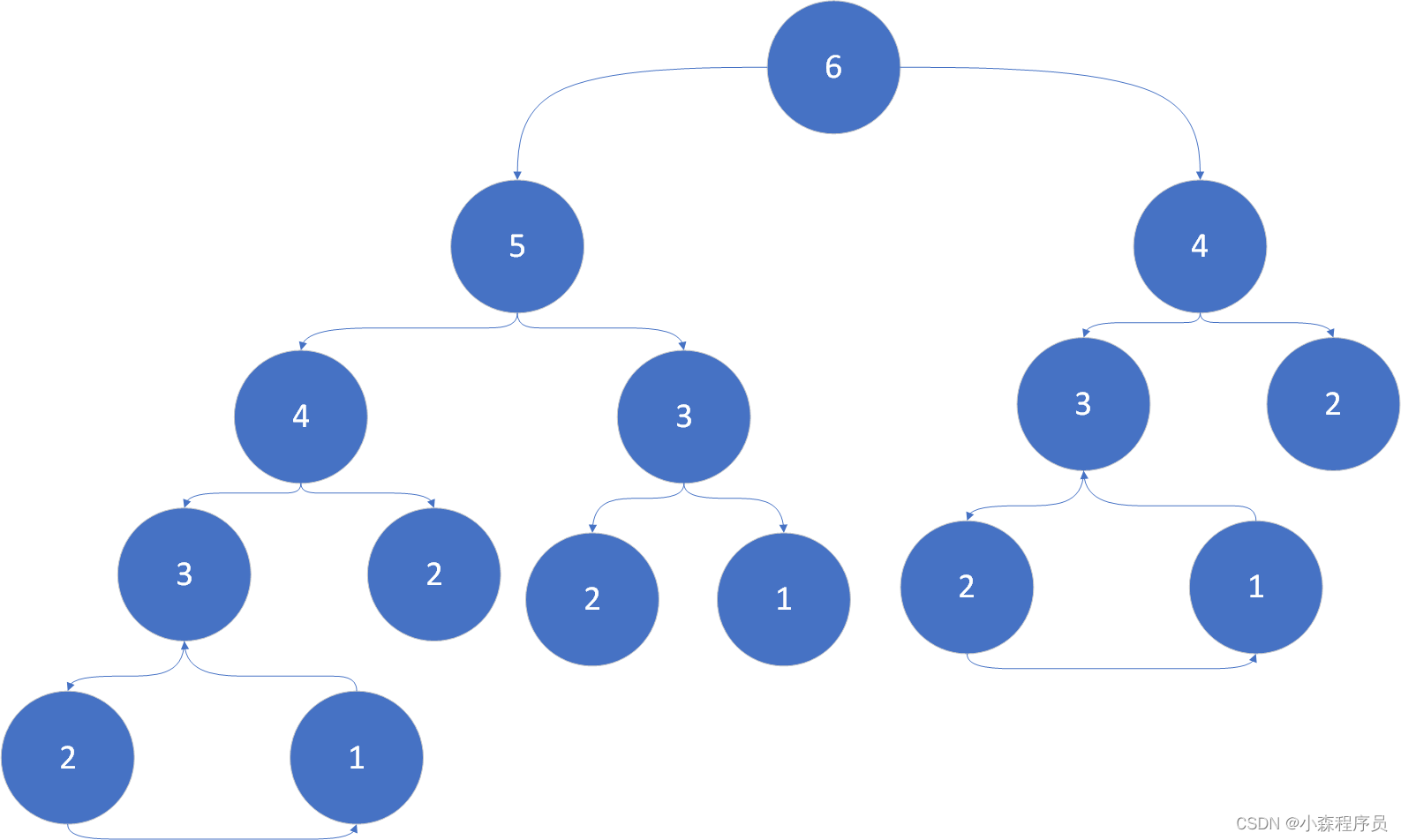
瞅了一眼：说到 怎么会有这么多重复的？ 坤坤非常疑惑，难道这就是分治法的复杂点？虽然说：分治思想对复杂的问题将拆成一个个小的子问题，并且得出原问题的解， 你会发现拆分成的子问题会越来越多 随着越来越多的子问题分为 效率就越低下 当得出n台阶 有多少种走法 的时候已经耗光了程序内存 因此 你会发现 “发现什么“
分而治之的算法是由上往下分析问题 “确实“ 那么有没有用极少的时间和空间，优化的算法？ 那就是接下来说的动态规划

动态规划算法核心思想

动态规划 ：定义一个存储空间的表， 存放重复的数据 ，并且达到解决子问题 的解
动态：可变的计算
规划：制定一些策略 （计算 并且返回的结果）

对于算法上的动态规划 来说：

1-算法可从下往上推出并且解决子问题
2 -定义可以重复使用并且便于子问题求解的空间
3 -制定一些策略 和方式达到求解问题的目的
4- 可适用于重复子问题才考虑范围之类

方式多种多样适合自己就行，但前提不要忘了定义：可以重复使用并且便于子问题求解的空间
也就是说不重复的子问题考虑不上 ：列如 ：二分查找法 没有相同的计算出的子问题

动态规划算法实现思路

分而治之的算法是由上往下分析问题 那么我们可以从下往上分析

什么叫从下往上分析呢 ，哎嘿，所谓的从下往上 就是从1开始到n
n=6 一到n 的走法 而不是n到1的走法
n
假设n=3 那么推到的计算为 1 + 2 =3

n=4 ，1+2 2+3 3+4
那么特殊情况就是 n=1 返回结果1 n=2 返回结果2
n=3 的话那么就是 n = n-1 +n-2 ？ 但 这个n不可以变化 所以说 动态规划的第一步来了
2- 定义可以重复使用并且便于子问题求解的空间
space 空间定义啥数据结构？ n = n-1 +n-2 ？ 想一想他需要的是顺序并且方便于操作 链表：我？ 不，顺序表 ：我才对
链表： 不好意思啊 抱歉 居然是用的是 顺序表 那么没啥好 焦虑的 直接一个循环就办到的事情
所以没啥可焦虑的了

首先记录 当然数组下标 space【0】=0；space【1】=1；space【2】=2；

3 -制定一些策略 和方式达到求解问题的目的
n=3
也就是循环处理space的数据直到 循环变量i结束 这个怎么知道结束？ 或者说i=3 i<n? 还是==3?
i<=n;

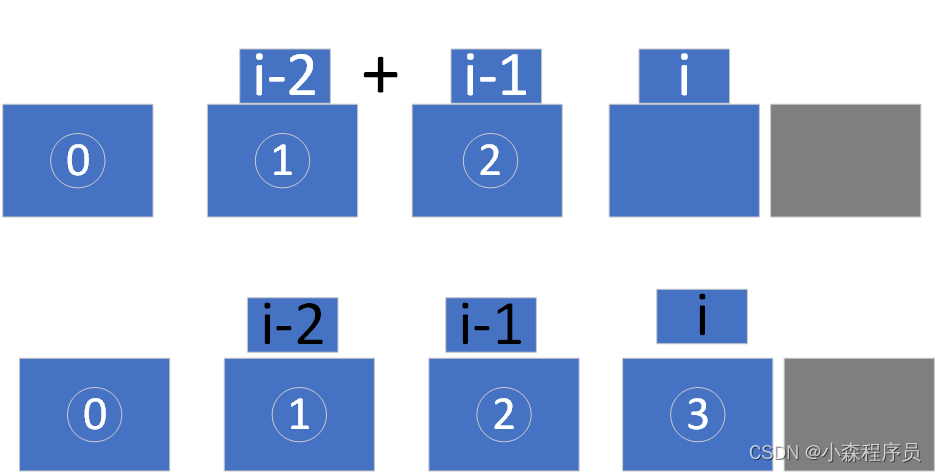
n=4的话 执行步骤

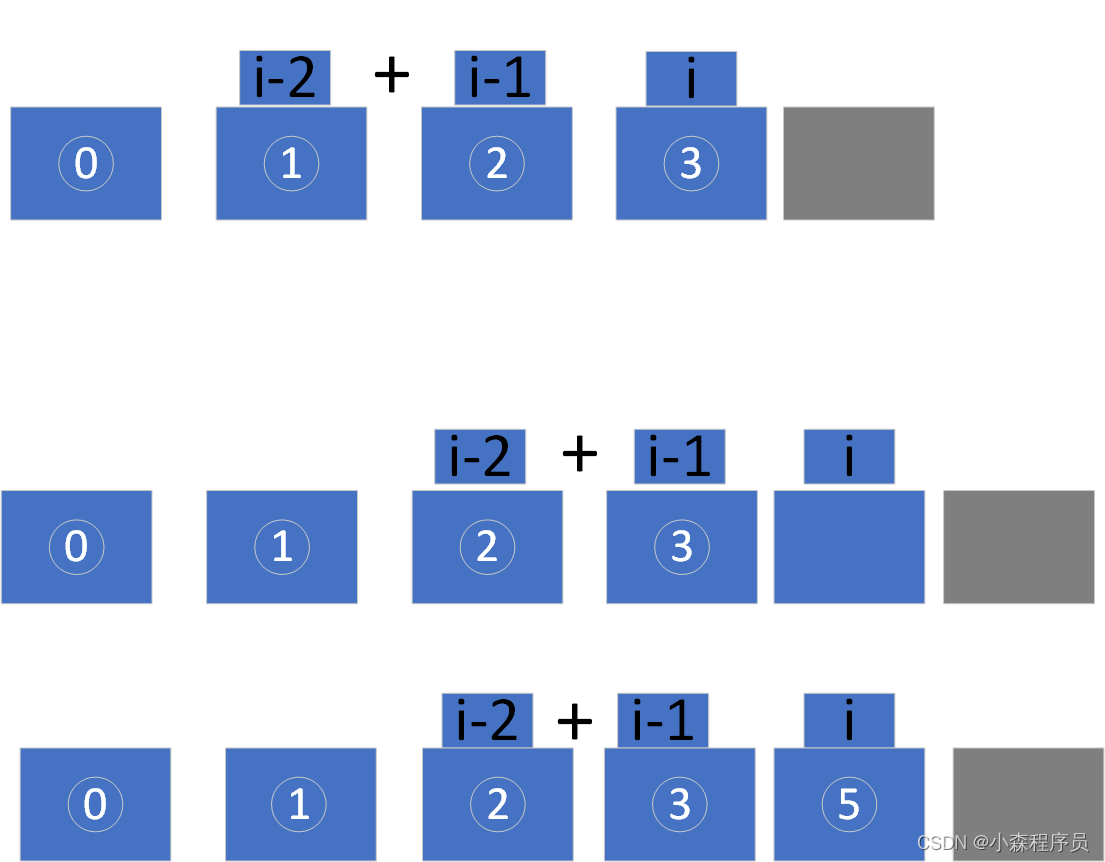
n=4 的结果5

动态规划应用算法专区

// 定义一个函数，名为TakeSteps_dp，输入一个整数n，返回一个整数  
int  // 定义函数返回类型为int  
TakeSteps_dp(int n) {  // 函数名称为TakeSteps_dp，输入参数为int类型的n  
  
 // 如果输入的n小于或等于0，直接返回0  
 if (n <= 0) {  // 判断条件：如果n小于或等于0  
 return 0;  // 返回0  
 }  
  
 // 定义一个整数变量ret，用于存储最后的结果  
 int ret;  // 定义一个整数变量ret  
  
 // 为n+1大小的数组分配内存，并用新分配的内存地址赋值给变量space  
 int* space = new int[n + 1];  // 动态分配一个大小为n+1的整型数组，并把它的首地址赋值给指针变量space  
  
 // 根据n的值进行不同的处理，这实际上是一个switch-case语句，但由于switch语句需要整数或枚举类型，所以这里使用了if-else结构  
 switch (n) {  // 判断条件：如果n的值等于某个特定的整数值  
  
 // 如果n等于1，则直接返回1，即只有一个台阶时，只有一种走法：走1步上台阶  
 case 1:  // 如果n的值等于1  
 ret = 1;  // 把1赋值给ret  
 break;  // 跳出switch语句  
  
 // 如果n等于2，则直接返回2，即有两个台阶时，有两种走法：走1步上台阶再走1步上台阶；或者直接走2步上台阶  
 case 2:  // 如果n的值等于2  
 ret = 2;  // 把2赋值给ret  
 break;  // 跳出switch语句  
  
 // 对于其他情况，执行以下操作，即当有3个或更多台阶时的情况  
 default:  // 如果n的值不等于1也不等于2，则执行default下面的语句  
  
 // 将space[0]、space[1]和space[2]分别赋值为0、1和2，初始化数组的前三个元素，表示走0步、走1步和走2步上台阶的方法数  
 space[0] = 0;  // 把0赋值给space数组的第一个元素space[0]，表示走0步上台阶的方法数（实际上就是不走）  
 space[1] = 1;  // 把1赋值给space数组的第二个元素space[1]，表示走1步上台阶的方法数（实际上就是只走一步）  
 space[2] = 2;  // 把2赋值给space数组的第三个元素space[2]，表示走2步上台阶的方法数（实际上就是只走两步）  
  
 // 从i=3开始到n，执行以下循环，这个循环实际上是计算走台阶的方法数  
 for (int i = 3; i <=n; i++) {  // 从i=3开始循环，直到i等于n的值（即台阶数）  
  
 // 每一级台阶的方法数是上一级台阶方法数与前两级台阶方法数的和，因为可以选择从上一级台阶跨一步上来或者从上两级台阶跨两步上来。  
 // 这里space[i-1]代表上一级台阶的方法数，space[i-2]代表上两级台阶的方法数。  
 space[i] = space[i - 1] + space[i - 2];  // 根据选择走法规则计算第i级台阶的方法数，并赋值给space数组的第i个元素space[i]  
 }  
  
 // 最终的结果存储在ret中，即space[n]，这里计算的是走完n个台阶的方法数  
 ret = space[n];  // 把space数组的第n个元素的值赋值给ret，即走完n个台阶的方法数。  
 break;  // 跳出switch语句。  
 }  
  
 // 释放之前分配的内存空间，避免内存泄漏。因为使用了new操作符分配内存，所以需要使用delete[]操作符释放内存。  
 delete[] space;  // 删除之前动态分配的数组，释放内存空间。  
   
 // 返回结果ret。由于这个结果是整数类型，所以需要用return关键字返回。  
 return ret;  // 作为函数的返回值返回结果ret。当输入一个整数n时，这个函数会返回一个整数