引言
胡图图:“我成为电脑砖家(人们都在我吧上评论电脑配置).,按理说我应该开一家图图计算机研究科技公司…”!
于小美:“没错,图图应该开一家公司 来扩展你的专业知识”
何壮壮:“厉害是厉害 ,要不要大哥来帮帮你(至于钱,好说:月薪2万)…”
图图:“你狮子大开口! ,那你还是当 你的音乐天才吧”!
壮壮:“还记得小时候,我胡说八道的建议,以及错误的引导 ,结果:还不是你自己(找到原因),并且说出来”
图图:“别提了 ,说说你的打算吧 刷子”
帅子:“我打算设计裙子 ,把我最讨厌的东西,设计起来,”
刷子:“还记得我们的美好的时光,土豆”
图图:“当然,我们一起玩 一起恶作剧, 一起上小学(有可能) …”
小美:“对我 没有印象?”
图图:“让我难以忘怀的就是我的兄弟 小怪 多少日日夜夜陪着我 唉 小怪!”
…
一番争吵后,图图陷入了沉思,是时候 把我的爱琴 深深地埋在心里…
这番描述有可能图图长大成人后, 毕竟图图已经是22岁了 ,刷子23岁 没错 刷子比图图大 当然是大3个月,这回忆杀有谁不爱呢
顺这整套逻辑可以画出 图结构

或许这才是真正的朋友关系图
这篇番外剧情打几分  ,通过这些了解图结构 恰到好处
,通过这些了解图结构 恰到好处
本来想写我们家的坤坤,但发现坤坤太多ikun粉丝.
尤其是哔哩哔哩全是以绿尸寒警告ikun们最为恰到好处,真的老绝了"尤其是把坤坤画出中国风的作为真ikun",和对接小曲真的老绝了,这两位真ikun ,我还想写让子弹飞这个正在申遗的文化遗产历史片作品 创作题材简直过多 !
图的原理
通过以上的例子,应该了解了图的描述以及刷子与土豆的 友情(男主角和女主角的友谊之情)
小森:确定不是"爱情的情?" 
来看看什么是图结构
图:由顶点( )和边(
)和边( )组合成的数据结构
)组合成的数据结构
- 顶点(Vertex):包含数据的结构
- 边(Edge):连接两个顶点的连接线(表示顶点的关系)

图图和小怪是兄弟关系,但只有图图知道小怪会说话 张帅子和图图是好哥们 并且知道小怪是图图的小猫 当然小怪的说话功能只有图图一个人知道,所以不存在小怪和张帅子的关系 可怜的小怪(就是不知道他俩搞起来暗恋) 痛! 太痛了呜呜
- 权值:是指描述关系或者解释的数值
比如说:我从广州到北京的飞机需要400元的机票 这个是的权值最有用的地方之一

图的表示
有方向 和 无方向
有方向

有方向的往往都是有一定的关系存在
比如说:"胡图图和张帅子之间的甜言密语 "
当着图图的面说 我可不是因为喜欢你才给你的 "(第三季的满天都是小星星(下))

网友神级翻译:"我可是因为喜欢你才给你的 " 哎呦我去,嗑死我了

网友:看个动画片都在撒狗粮 呜呜
图图:**emmmm,我不知道刷子在说什么? 你再说一遍! **
他爸妈以及小怪都不知道;
这种情况也就有了无方向的
无方向

蔡徐坤(2019 NBA中国形象大使) 臭名昭著
一旦公之于众必然骂声一片 什么香精煎鱼 ,拿什么荔枝 食补食油饼 提供了一系列的食物 当然最重大的食物:鸡你太美
吃鸡族疯了似的 ,加上这份绿尸寒 你可真牛逼 立马就扒出来
"在偶像练习生打篮球的鸡哥 在哪里疯狂唱跳Rap 并且打起来坤式篮球 " 一场ikun大战即将打响 小黑子们想出来"香精煎鱼 ,拿什么荔枝 食补食油饼 "提供了一系列的食物 后 停止了攻击
当然这些ikun没有丢坤坤的脸 拿出二创作品 并且一个比一个牛逼,至于本作者我吗 当然是记录这些ikun们的,以及这些菜
我没有侮辱蔡徐坤本人吧 ! 你们统一在评论区讨论讨论
你们也看出来,我需要表示什么,这些就是某粉丝群体对蔡徐坤本人喜欢的程度(一本正经的胡说八道)
某粉丝群体喜欢蔡徐坤的梗 ,并不是喜欢蔡徐坤 , 利用蔡徐坤的正面大新闻来调侃,引起了轰动B站用户( 大部分)
从恨变灵感大爆发 各种二创作品,真的老牛逼了,尤其是鬼畜区的 也给蔡徐坤一定的知名度 (希望入站必刷能出现我坤哥的鬼畜视频) 我说的这些就是对这个无向图的了解以及我是怎么描述它仅此而已
当然也可以从篮球队说起对于篮球队的话 中国篮球队Vs美国篮球队 (假设) 他们并没有关系 与国家有关系 其次是篮球 因为热爱篮球 在这里就体现出无向图
到此为止 我萌理解了有方向和无方向的图 接下来就是如何表示这些 图结构
图的存储方式
邻接矩阵

我们来看这张图 A到F 的 图结构
首先 我们看A 这个名号叫菠萝吹雪的 他有三个女人 分别为"菠萝小薇",“梨花诗”,“梨花诗(橙留香)”
B就是"菠萝小薇" 虽然非常不情愿,但自己还是喜欢上另外一个男人F
**C 是梨花诗(配音:橙留香的配音演员(陆双)) ** 原来泡自己的兄弟
“D是 梨花诗(如花)”
"E:好兄弟(橙留香)
所谓的F 小果叮
用 邻接矩阵 表示是这样子的

行 : A行 B行 C行 D行 E行 D行
列 : A列 B列 C列 D列 E列 D列
简化一下
A是喜羊羊 B是美羊羊 C是沸羊羊 大家应该:长大 看喜灰 发现大家都觉得 沸羊羊像舔狗 单独的片段:来自B站
好友表示:1
喜欢表示:2
舔狗表示:3


喜羊羊:
A行 A列 喜羊羊 自己
A行 B列 美羊羊 好友
A行 C列 沸羊羊 好友(以及好兄弟)
美羊羊:
B行 A列 喜羊羊 喜欢
B行 B列 美羊羊 自己
B行 C列 沸羊羊 舔狗
沸羊羊:
C行 A列 喜羊羊 好友(以及好兄弟)
A行 B列 美羊羊 喜欢
A行 C列 沸羊羊 自己
如何? 这个形象 (怎么感觉熊出没也有呢) 哈哈哈 当然熊出没那个真兄弟,
emmm 你们发现了 加入一个人会使得空间大了 3个人 九个空间 那加个人 岂不是扩大 加顶点 再3乘4? 还是4乘4 ? 这个空间大
很明显是4乘4
假设果宝特攻里有第五位cp 还得添加顶点 并且多出来顶点 (n*2) -1个顶点 因此通常不会用到邻接矩阵
空间和时间:复杂度为
V: (Vertex 顶点) 顶点数
| 操作 | 复杂度 |
|---|---|
| 存储空间 | O(V^2) |
| 添加顶点 | O(V^2) |
| 添加边 | O(1) |
| 访问 | O(1) |
邻接表

这图怎么感觉有点像哈希表?
但指向的是关联的数据
我来画个简单的 以刺客伍六七的一部分的角色 来进行描述吧 最近看的国产动漫.
主角:伍六七原本是暗影刺客 ,遭遇某些事情被通缉了 结果被杀害 ,漂流到小鸡岛,被一只蓝羽鸡 名叫鸡太保,所救 因为他的救治使活过来了…
梅花十三:因为某些原因,阴差阳错的 与伍六七接吻 所以成了CP.当然他是暗影刺客的之一的徒弟 同样是敌人
鸡太保:一只备受压迫的蓝羽鸡,但肯反抗,亲眼见证自己的兄弟活活被打死,却不敢给小飞鸡知道真相. 后来一起来到小鸡岛…
小飞鸡:蓝羽鸡和白鸽的爱情结晶,他知道他的爸以去世 使得他强大起来 被鸡太保照顾着 使他有安全感 并且拥有男生羡慕的八块腹肌(当有人被欺负时变得)
可乐:一名斯坦国的基因实验品 同时也是异能者 异能属性:让对方无法动弹
何大春: 小鸡岛保镖 保护小鸡岛安全,但因为排斥来到小鸡岛 技能:情比金坚七天锁 金刚不坏童子身 金刚不坏大宝剑
可以看出都在反映社会 这些角色有亲情 友情 还有 爱情 因此可以说是青春期 包括成人 必追的动漫 

在这里可以看到弄了一个角色分析池

然后 依次添加关系
这是伍六七添加的关系

这是鸡太保添加的关系

这是小飞鸡添加的关系

这是梅花十三添加的关系

这是可乐添加的关系

这是何大春添加的关系

可以看出以下的关系数量

| 顶点 | 边 |
|---|---|
| A | 6 |
| B | 2 |
| C | 2 |
| D | 1 |
| E | 1 |
| F | 1 |
可以看出顶点 A到F顶点 ,边 的数量
邻接表是通过大规模的数量 顶点 与关系边 一个列表可以用不同的顶点链接成边
空间和时间:复杂度为
V: (Vertex 顶点) 顶点数 E(Edge) 边数
| 操作 | 复杂度 |
|---|---|
| 存储空间 | O(V+E) |
| 添加顶点 | O(1) |
| 添加边 | O(1) |
| 访问 | O(V) |
图的算法实现
先看 定义邻接表
//边
struct Edge {
int AdjVertex;//邻接顶点
int Weight;//权值
Edge* next;//下一条边
};
using VertexValue = use define
//顶点
struct Vertex {
VertexValue value; // 顶点数据
Edge* First;//获取第一条边
};
//邻接顶点
using AdjVertex = Vertex*;
//邻接表
using AdjList = AdjVertex*;
//图
struct Graph {
//邻接列表
AdjList List;
//顶点数
int VertexSize;
//边数
int EdgeSize;
};
看的清清楚楚 !
using AdjVertex = Vertex*;
你也可以不用指针 用 了也没啥事我的就是方法方式不一样
为了更好的构建图结构 画图是避免不了的事情
请看现露出只因(鸡)脚,本作者 带来的精彩图

首先来看圆圆的带着字 ! 蔡徐坤与其他人关系 是没有任何的关系
邻接表:包含数据 并且有一个 Edge* First; 获取第一条边 当然现在也显示不出来
来看看邻接表如何组合成图结构的吧
//图
struct Graph {
//邻接列表
AdjList List;
//顶点数
int VertexSize;
//边数
int EdgeSize;
};
//邻接列表
AdjList List; //本质就是 一个指针数组 List指向蔡徐坤这个虚拟结点 当然你也可以认为是一个结点指向蔡徐坤这个结点

算法实现
算法声明
//图初始化
void GraphInit(Graph& graph);
//添加顶点
void AddVertex(Graph& graph, VertexValue value);
//添加边
void AddSingleEdge(Graph& graph, VertexValue VertexValueFirst, VertexValue VertexValueSecond);
//添加边的权值
void SetEdgeOFWeight(Graph& graph, VertexValue VertexValueFirst, VertexValue VertexValueSecond, Ikun Weight);
//深度优先遍历
void DepthFirstSearch(const Graph& graph);
void DepthFirstSearch(const Graph& graph, int VertexIndex);
//广度优先遍历
void BreadthFirstSearch(const Graph& graph);
初始化图结构
你需要多少个顶点 ?
看你的需求 定义常量
所以添加顶点的的时候 动态? 还是一次性分配好
当然 效率来说当然是还是一次性分配好 难道你想一个个扩展? 产生时间成本 有的时候一切的安排或许有效率 但也要学会变动态,比如说:突然忘记带笔记本电脑上班,赶紧回去找笔记本电脑 没有发生什么事情 .比如说 :遇见好久不见的朋友 聊一下什么的 我们需要理性的动态 而不是一边一次性安排计划 这个点我要干嘛 ;只会感觉没有意义 完全是计划绑定死了的人
所以一切看你的需求来 我的需求是 如果顶点数大于1024 那么不需要添加
//顶点添加最大值
const int MaxSize = 1024;

//邻接表初始化
static void AdjListInit(AdjList& List) {
//遍历邻接表数组
for (size_t i = 0; i < MaxSize; i++) {
//初始化所有元素为null
List[i] = nullptr;
}
}
//图初始化
void GraphInit(Graph& graph){
//动态分配邻接表数组
graph.List = new AdjVertex[MaxSize];
//调用邻接表初始化函数
AdjListInit(graph.List);
//初始化顶点数量和边数量
graph.VertexSize = 0;
graph.EdgeSize = 0;
}
添加顶点
static AdjVertex CreateAdjVertex(VertexValue& value) {
//创建新顶点
Vertex *vertex = new Vertex;
//设置顶点的值
vertex->value = value;
//设置第一条边为null
vertex->First = nullptr;
//返回邻接顶点,实际上就是新顶点的指针
return vertex;
}
void AddVertex(Graph& graph, VertexValue value){
//获取顶点数量的引用
int& VertexSize = graph.VertexSize;
//如果顶点数量达到上限,不再添加
if (VertexSize >= MaxSize) {
return;
}
//获取邻接表的引用
AdjList& List = graph.List;
//调用CreateAdjVertex创建新顶点
AdjVertex adjVertex = CreateAdjVertex(value);
//将新顶点添加到邻接表中
List[VertexSize] = adjVertex;
//更新顶点数量
++VertexSize;
}
添加顶点非常像顺序表添加一样简单
真正的man,不需要绽放光芒也能闪亮

添加完毕后的 图结构:

感觉有点枯燥起来,唉 也不知道为啥总觉得自己提高不上来,可能过于自信了吧 不管怎么样实力永远都是比比不了学历 这我知道,但尝试过去休闲日子,因为自己太失败了,一个不太正常的人,当然我说的是我本人 但有的时候有点怪 怎么说呢看看这个链接我的故事
唉 避免不了的事情 就是这件事情 我虽然放弃了我的学业 当然学习的机会是自己争取,当然这怎么可能一个人呢 当然资源
竞争往往都是给别人,但我敢于投资策略 ,总之一切靠的是人脉网络 我其实写这个博客就是需要这些人脉网络扩大我的就业机遇这才是目的,谢谢你们关注 ,我会继续更新所学到的内容 以及分享一些有趣的话题
添加边
//寻找对应的顶点的索引
static int Location(Graph& graph, VertexValue & value){
const int VertexSize = graph.VertexSize;
for (size_t i = 0; i < VertexSize; i++){
//检查当前顶点的值是否与value相等
const bool result = graph.List[i] ? graph.List[i]->value == value : false;
if (result){
return i;
}
}
return VertexSize;
}
//创建一条新的边
static Edge* CreateEdge(int &AdjVertex,Edge *& First) {
Edge* Newedge = new Edge;
//设置新边的终点顶点索引
Newedge->AdjVertex = AdjVertex;
//将新边插入到第一条边之前
Newedge->next = First;
return Newedge;
}
//将新边插入到邻接表中
static void EdgeLink(Edge* &edge, Edge*& newEdge) {
edge= newEdge;
}
//向图中添加一条边 (- graph: 图的结构体,包含顶点数、边数、邻接表等信息 - VertexValueFirst: 个顶点的值- VertexValueSecond: 第二个顶点的值)
void AddSingleEdge(Graph& graph, VertexValue VertexValueFirst, VertexValue VertexValueSecond) {
const int VertexSize = graph.VertexSize;
int& EdgeSize = graph.EdgeSize;
//查找第一个顶点的索引
int VertexValueFirstIndex = Location(graph, VertexValueFirst);
//查找第二个顶点的索引
int VertexValueSecondIndex = Location(graph, VertexValueSecond);
//如果两个顶点都存在
if (VertexValueFirstIndex != VertexSize && VertexValueSecondIndex != VertexSize) {
//获得第一个顶点
Vertex* VertexFirst = graph.List[VertexValueFirstIndex];
//获得第一个顶点的首条边
Edge* ¤tEdge = VertexFirst->First;
//创建一条新边
Edge* NewEdge = CreateEdge(VertexValueSecondIndex, currentEdge);
//将新边插入到邻接表中
EdgeLink(currentEdge, NewEdge);
++EdgeSize;
}
}

由于边是单向链表 所以前插入法最高效,若你是看不懂需要 复习图的技术点-里的邻接表部分
int AdjVertex;//邻接顶点 代表 邻接表的索引
看深度优先遍历就知道

依次添加后

自定义函数依次添加边 这是演示 一般开发不使用中文命名函数 你们也知道
void 四大ikun连接蔡徐坤(Graph &Graph, VertexValue value[]) {
for (size_t i = 1; i <= 4; i++) {
AddSingleEdge(Graph, value[i], value[0]);
}
}
void 四大ikun互相连接(Graph &Graph, VertexValue value[]) {
AddSingleEdge(Graph, value[1], value[2]);
AddSingleEdge(Graph, value[1], value[3]);
AddSingleEdge(Graph, value[1], value[4]);
AddSingleEdge(Graph, value[2], value[1]);
AddSingleEdge(Graph, value[2], value[3]);
AddSingleEdge(Graph, value[2], value[4]);
AddSingleEdge(Graph, value[3], value[1]);
AddSingleEdge(Graph, value[3], value[2]);
AddSingleEdge(Graph, value[3], value[4]);
AddSingleEdge(Graph, value[4], value[1]);
AddSingleEdge(Graph, value[4], value[2]);
AddSingleEdge(Graph, value[4], value[3]);
}
可能链接可能乱七八糟了 我们不需要理会
接下来说一下深度优先遍历可能需要有段时间 准备! 就这样吧
深度优先遍历
struct DepthFirstSearchFLag {
int index; //当前访问顶点的索引
bool visited[MaxSize]; //标记数组,MaxSize为图的最大顶点数
};
//深度优先搜索遍历图
static void DepthFirstSearch(const Graph& graph, DepthFirstSearchFLag &flag) {
//当前访问的顶点索引
int& index = flag.index;
//如果当前顶点已被访问,返回
if (flag.visited[index]) {
return;
}
//输出当前顶点的值和权重
cout << graph.List[index]->value << " "<< " is " << (graph.List[index]->First->Weight == Ikun::TrueIKun ? " Ikun : " : " kun : ") << graph.List[index]->First->Weight << endl;
//标记当前顶点为已访问
flag.visited[index] = true;
//获得当前顶点的首条边
Edge* current = graph.List[index]->First;
//下一条边的终点顶点索引
int nextIndex;
//遍历邻接表
while (current) {
//获得下一条边的终点顶点索引
nextIndex = current->AdjVertex;
//移到下一条边
current = current->next;
//如果下一顶点未被访问
if (!flag.visited[nextIndex]) {
//访问下一顶点
index = nextIndex;
//递归调用
DepthFirstSearch(graph, flag);
}
}
}
//深度优先搜索图,使用递归实现
void DepthFirstSearch(const Graph& graph) {
//定义结构体,保存搜索状态
//index:当前访问顶点索引
//visited[]:标记所有顶点是否被访问,初始化为false
DepthFirstSearchFLag Flag = {};
//获取图的顶点数
const int VertexSize = graph.VertexSize;
//遍历图的所有顶点,i为顶点索引
for (size_t i = 0; i < VertexSize; i++) {
//如果当前顶点i未被访问
if (!Flag.visited[i]) {
//1. 设置当前顶点索引为i
Flag.index = i;
//2. 递归调用,访问当前顶点i
//在递归调用中,会完成如下操作:
//2.1 输出当前顶点i信息
//2.2 标记当前顶点i为已访问
//2.3 遍历当前顶点i的邻接表
//2.4 如果发现未访问顶点,递归调用访问之
//2.5 返回上一层调用
DepthFirstSearch(graph, Flag);
}
}
//遍历结束,输出一个换行
cout << endl;
}
深度优先遍历图

进入第一次递归:

返回上一层:

进入第二次递归

返回上一层:


进入第三次递归

返回上一层:


进入第四次递归

返回上一层:

循环结束
深度优先遍历结果

- 检查当前顶点是否被访问,如果是则返回。否则打印顶点信息。
if (flag.visited[index]) {
return;
}
cout << graph.list[index]->value << " ";- 将当前顶点标记为已访问。
flag.visited[index] = true;- 指向当前顶点的第一个相邻顶点。如果未访问,则将其索引赋值给index,递归调用深度优先搜索算法。
Edge* current = graph.list[index]->first;
while (current) {
int nextIndex = current->adjVertex;
if (!flag.visited[nextIndex]) {
index = nextIndex;
depthFirstSearch(graph, flag);
}
current = current->next;
}- 直到所有相邻顶点都被访问,返回。重复此过程直到图被完全遍历。
广度优先遍历
static void BreadthFirstSearch(const Graph& graph, BreadthFirstSearchFLag& flag) {
queue<int> vertexIndexQueue;
int& Index = flag.index;
vertexIndexQueue.push(Index);
bool(&visited)[MaxSize] = flag.visited;
while (!vertexIndexQueue.empty()) {
Index = vertexIndexQueue.front();
Edge* current = graph.List[Index]->First;
vertexIndexQueue.pop();
if (!visited[Index]) {
cout << graph.List[Index]->value << " ";
if (current) {
cout << " is First Edge :" << current->AdjVertex << " Weight: " << (current->Weight == Ikun::TrueIKun ? " Ikun : " : " kun : ") << current->Weight << endl;
}
visited[Index] = true;
}
int NextIndex;
while (current) {
NextIndex = current->AdjVertex;
current = current->next;
if (!visited[NextIndex]) {
vertexIndexQueue.push(NextIndex);
}
}
}
}
void BreadthFirstSearch(const Graph& graph){
BreadthFirstSearchFLag Flag = {};
const int VertexSize = graph.VertexSize;
for (size_t i = 0; i < VertexSize; i++) {
if (!Flag.visited[i]) {
Flag.index = i;
BreadthFirstSearch(graph, Flag);
}
}
cout << endl;
}
广度优先遍历图




- 从起点顶点开始,其索引push入队列q,visited数组对应位置置true。
q.push(start);
visited[start] = true;- 队首元素出队,此时index指向当前访问顶点。
int index = q.front();
q.pop();
- 访问此顶点,打印信息。
cout << graph.list[index]->value << " ";
// 打印相邻顶点信息- 当前顶点的相邻顶点索引入队,对应visited位置置true。循环直到相邻顶点为空。
Edge* current = graph.list[index]->first;
while (current) {
int adj = current->adjVertex;
if (!visited[adj]) {
q.push(adj);
visited[adj] = true;
}
current = current->next;
}- 重复步骤2到4,直到队列为空。算法结束。
图的导航-最短路径算法
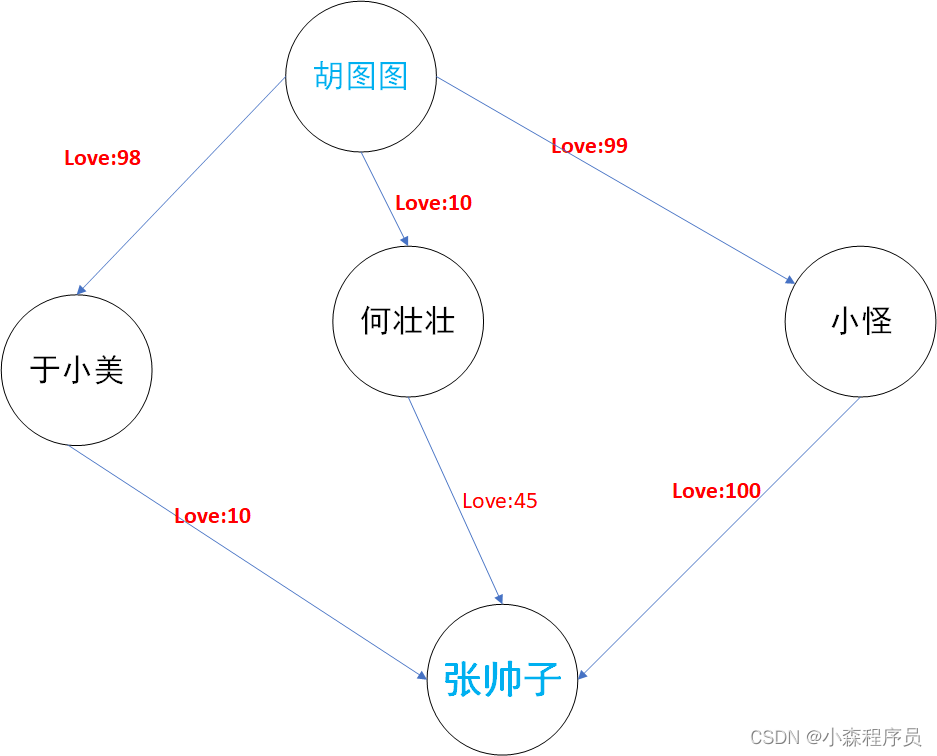
一个 恋爱关系图
胡图图love:98于小美
胡图图love:48何壮壮
胡图图love:99小怪
于小美love:10张帅子
何壮壮love:45张帅子
小怪love:100张帅子
胡图图到张帅子的最短路径
确定不是恋爱路径?
算法实现
先看猛料再看是否实现思路
// 定义深度优先搜索状态
struct DepthFirstSearchFLag {
int index; // 当前索引
bool visited[MaxSize]; // 顶点访问状态
};
// 定义最短路径状态
struct ShortPathFLag {
DepthFirstSearchFLag Flag; // 深度优先搜索状态
int end; // 结束顶点索引
int stepNum; // 步数
int m_Weight; // 当前路径权重
int ArgsWeight; // 参数路径权重
int SevePath[MaxSize]; // 保存路径
int ShortPathValue[MaxSize];// 最短路径值
};
void ShortPath(const Graph& graph, ShortPathFLag &ShortPathFLag) {
int& index = ShortPathFLag.Flag.index;
int& end = ShortPathFLag.end;
auto& visited = ShortPathFLag.Flag.visited;
auto& SevePath = ShortPathFLag.SevePath;
auto& ShortPaths = ShortPathFLag.ShortPathValue;
int& stepNum = ShortPathFLag.stepNum;
int& ArgsWeight = ShortPathFLag.ArgsWeight;
int& Weight = ShortPathFLag.m_Weight;
if (index==end){
for (size_t i = 0; i < stepNum; i++) {
cout << graph.List[SevePath[i]]->value << " ->"; //输出路径
}
cout <<"\t该路径对应的恋爱值 (Love)是:" << ArgsWeight << endl; // 输出对应路径长度
if (Weight < ArgsWeight){
Weight = ArgsWeight;
int conut = stepNum * sizeof(conut);
memcpy(ShortPaths, SevePath, conut);
ArgsWeight = 0;
}
}
int currentIndex = index;
visited[index] = true;
Edge* current = graph.List[index]->First;
while (current) {
currentIndex = current->AdjVertex;
if (!visited[currentIndex]){
visited[currentIndex] = true;
int currentWeight = current->Weight;
SevePath[stepNum++] = currentIndex;
ArgsWeight = ArgsWeight + currentWeight;
index = currentIndex;
ShortPath(graph, ShortPathFLag);
visited[currentIndex] = false;
SevePath[--stepNum] = 0;
}
current = current->next;
}
}
void ShortPath(const Graph& graph, VertexValue VertexValueFirst, VertexValue VertexValueSecond){
ShortPathFLag Flag{};
Flag.m_Weight = 0;
const int VertexSize = graph.VertexSize;
Flag.Flag.index = Location(graph, VertexValueFirst);
Flag.end = Location(graph, VertexValueSecond);
if (Flag.Flag.index != VertexSize && Flag.end!= VertexSize) {
cout << VertexValueFirst << "到" << VertexValueSecond << "最短路径:" << endl;
ShortPath(graph, Flag);
cout << endl;
cout << VertexValueFirst << "到" << VertexValueSecond << "最短路径为恋爱总值:" << Flag.m_Weight << endl;
cout << "路径:"<< VertexValueFirst<<" ";
auto& Path = Flag.ShortPathValue;
int i = 0;
while (i < MaxSize && Path[i]>0) {
cout <<"-> " << graph.List[Path[i]]->value << " ";
i++;
}
cout << endl;
}
}
算法思想
- 获取状态信息,包括当前索引、终点索引、步数等。
int& index = ShortPathFLag.Flag.index;
int& end = ShortPathFLag.end;
auto& visited = ShortPathFLag.Flag.visited;
auto& SevePath = ShortPathFLag.SevePath;
auto& ShortPaths = ShortPathFLag.ShortPathValue;
int& stepNum = ShortPathFLag.stepNum;
int& ArgsWeight = ShortPathFLag.ArgsWeight;
int& Weight = ShortPathFLag.m_Weight;- 如果到达终点,更新最短路径并输出。
if (index==end){
//输出路径
//更新最短路径
}- 获取当前顶点的相邻未访问顶点。
int currentIndex = index;
Edge* current = graph.List[index]->First;
while (current) {
currentIndex = current->AdjVertex;
if (!visited[currentIndex]){
//找到相邻未访问顶点
}
current = current->next;
}- 标记顶点为已访问,更新路径和权重,继续搜索。
visited[currentIndex] = true;
SevePath[stepNum++] = currentIndex;
ArgsWeight = ArgsWeight + current->Weight;
index = currentIndex;
ShortPath(graph, ShortPathFLag);
- 搜索返回后重置状态,继续遍历其他相邻顶点。
visited[currentIndex] = false;
SevePath[–stepNum] = 0;
最短路径算法图

递归调用
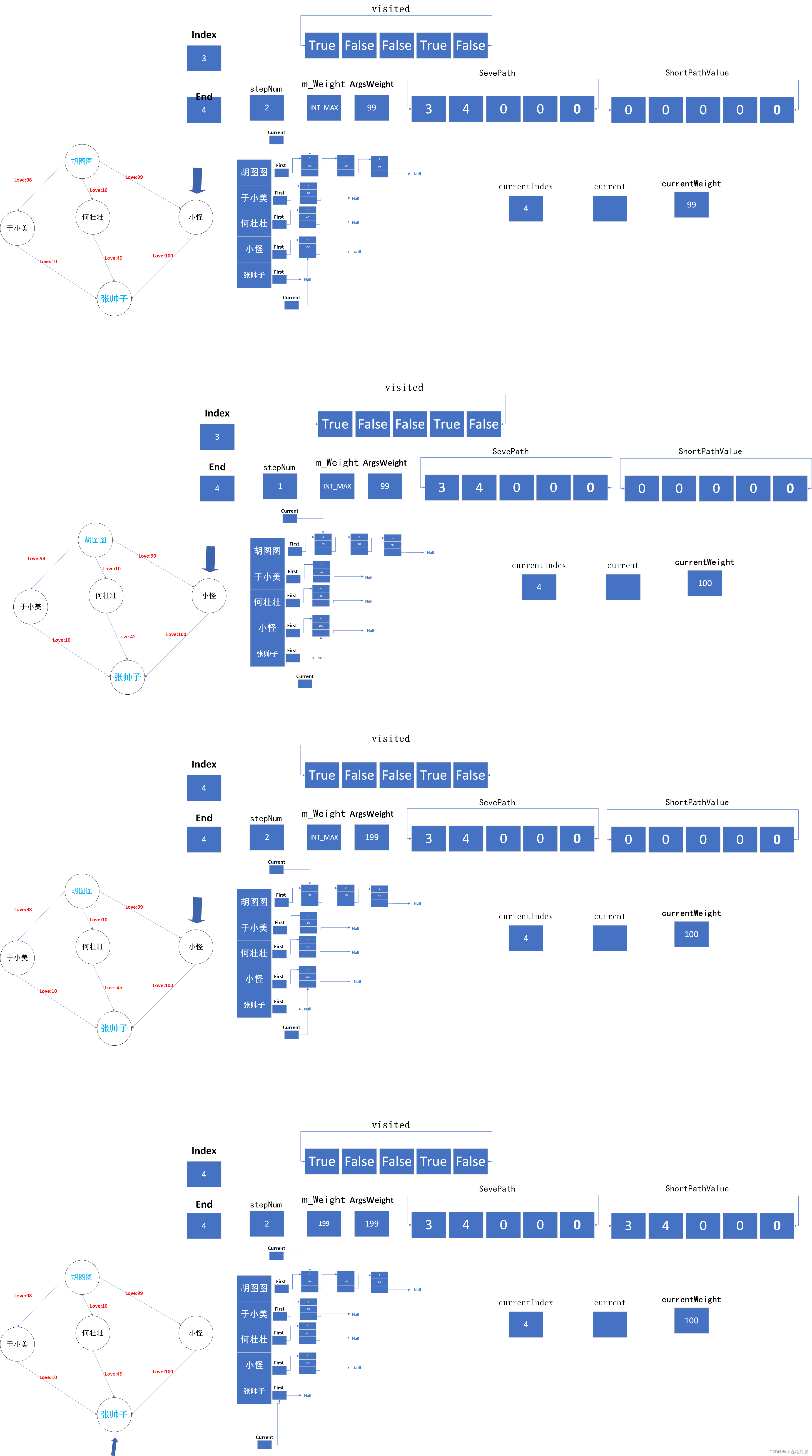
返回上一层递归
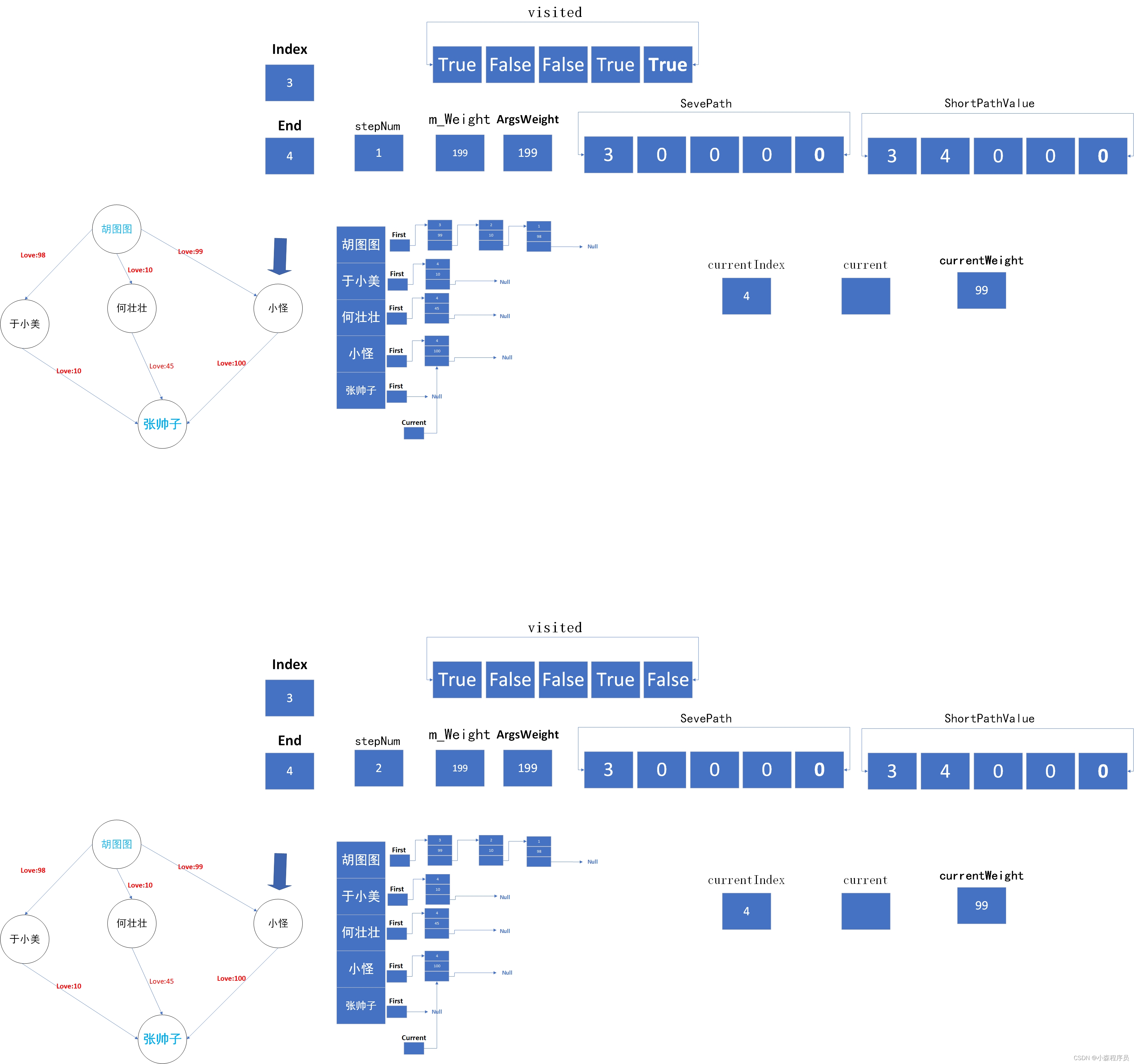
结果
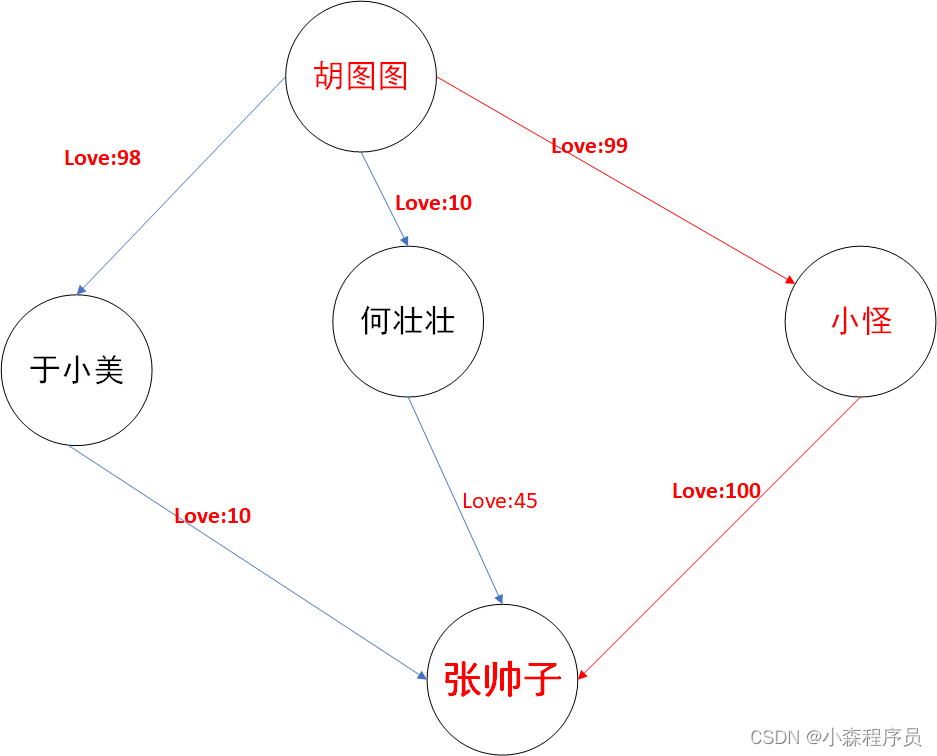
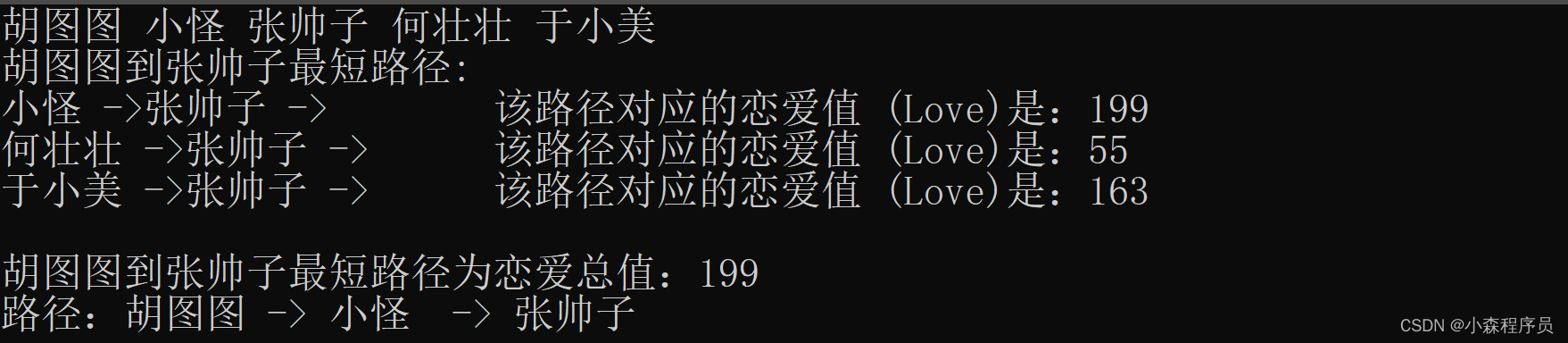





 本文详细介绍了图的概念,包括有向和无向图,通过邻接矩阵和邻接表两种方式表示图结构。接着,展示了如何使用C++实现图的深度优先遍历和广度优先遍历,并探讨了最短路径算法在恋爱关系图中的应用。此外,文章还以蔡徐坤为例,讨论了粉丝群体的网络行为和情感连接。
本文详细介绍了图的概念,包括有向和无向图,通过邻接矩阵和邻接表两种方式表示图结构。接着,展示了如何使用C++实现图的深度优先遍历和广度优先遍历,并探讨了最短路径算法在恋爱关系图中的应用。此外,文章还以蔡徐坤为例,讨论了粉丝群体的网络行为和情感连接。




















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










