算法系列1——Kmeans聚类

K-means聚类算法（事先数据并没有类别之分！所有的数据都是一样的）

1 概述

K-means算法是集简单和经典于一身的基于距离的聚类算法

采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。

该算法认为类簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。

2 核心思想

通过迭代寻找k个类簇的一种划分方案，使得用这k个类簇的均值来代表相应各类样本时所得的总体误差最小。

k个聚类具有以下特点：各聚类本身尽可能的紧凑，而各聚类之间尽可能的分开。

k-means算法的基础是最小误差平方和准则,

其代价函数是：

![在这里插入图片描述](https://img-blog.csdnimg.cn/20210117194458809.png)


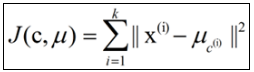
   式中，μc(i)表示第i个聚类的均值。

各类簇内的样本越相似，其与该类均值间的误差平方越小，对所有类所得到的误差平方求和，即可验证分为k类时，各聚类是否是最优的。

上式的代价函数无法用解析的方法最小化，只能有迭代的方法。

3 算法步骤

（1） 随机选取 k个聚类质心点
（2）计算每个点，与K个中心点的距离，然后将每个点聚集到与之最近的中心点
（3）新的聚集出来之后，计算每个聚集的新中心点
（4）迭代步骤2和步骤3，直至满足退出条件（条件有两个：
1聚类中心点不再变化，
2迭代次数达到某个值；
具体计算时，可以取其中一个条件，或者两个条件同时取到）

4 代码实现

import numpy as np
import matplotlib.pyplot as plt

# 计算两点之间的欧式距离
def distance(e1, e2):
    return np.sqrt((e1[0]-e2[0])**2+(e1[1]-e2[1])**2)

# 集合中心,arr是一个包含元组的列表，e就是一个二元组，e[0]是x,e[1]是y
def means(arr):
    return np.array([np.mean([e[0] for e in arr]), np.mean([e[1] for e in arr])])

# arr中距离a最远的元素，用于初始化聚类中心
def farthest