二叉树 概念和结构

1.树概念及结构

这些概念用来形象表示一个树

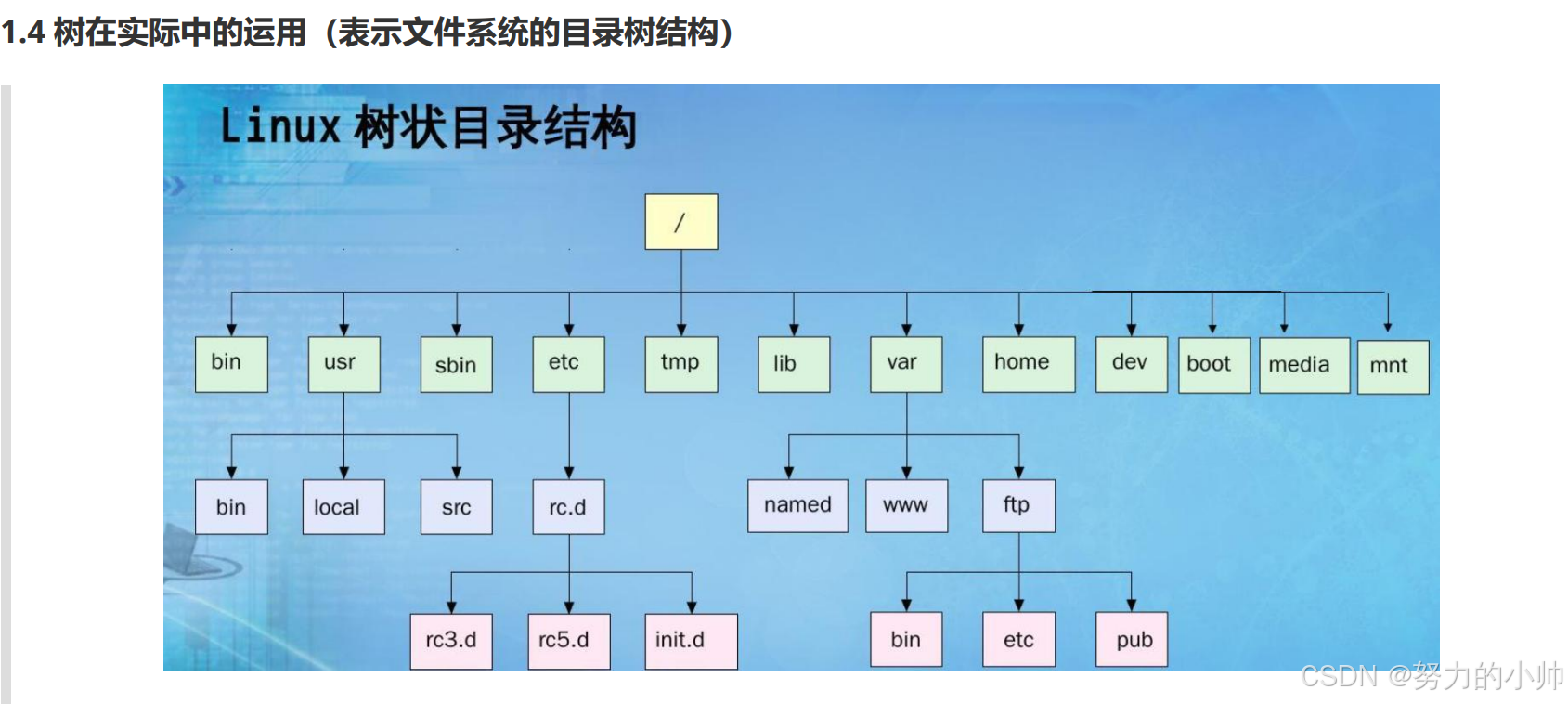
2.二叉树概念及结构

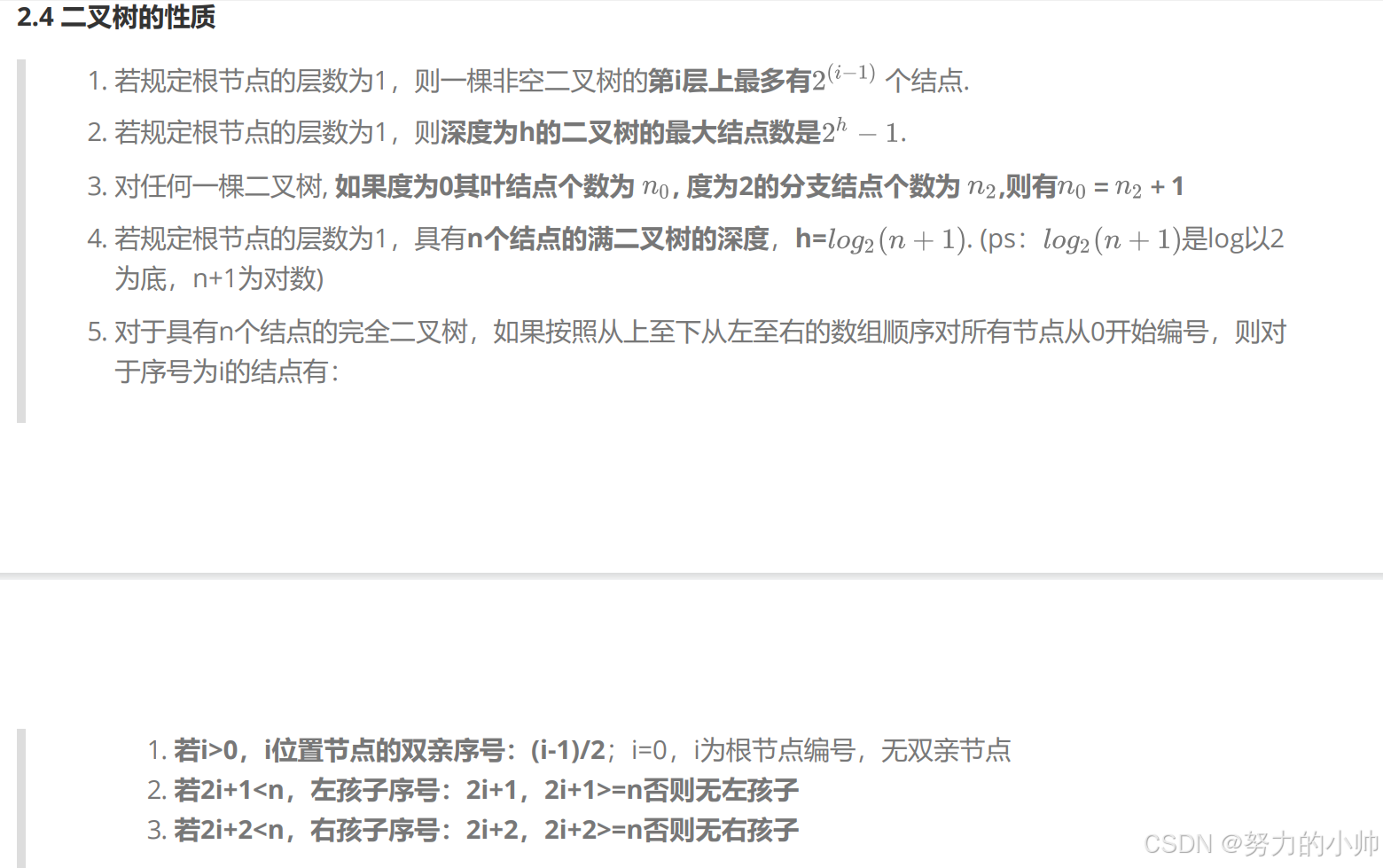
高度为h的完全二叉树，节点数量范围为[2^(h-1),2^h-1]

逻辑结构：想象出来的

物理结构：实实在在在内存中是如何存储的（就是树下面的数组）

表示二叉树的值在数组位置中父子与下标的关系

这里面父亲与孩纸有关系 ：parent = (child-1)/2     leftchild = parent*2+1  rightchild = parent*2+2;

可见数组存储二叉树会浪费许多空间  即只适合存储完全二叉树

在堆中插入元素时要操作的是数组   但在逻辑上看是操作的是二叉树

这种操作叫做向上调整  最多调整h次==logN次

冒泡排序O（N*N）

堆排序O（N*logN）

向下调整建堆： 从下向上看，调整次数少，节点个数多，到最后一多一少

向上调整建堆：从上向下看，调整次数少，节点个数少，到最后两个都多，

3.二叉树顺序结构及实现

堆都是完全二叉树

目前学的二叉树（普通）没有作用，用二叉树来存储数据就更高大上嘛？

我们之前学的数据结构先学的是增删查改   而二叉树不是

但我们给二叉树加一个性质就很有用了 查找*（左子树小于右子树） 搜索的效率很高

交换顺序就可以实现 不同的打印  ——》因为执行是顺序

二叉树是双路递归  

二叉树遍历_牛客题霸_牛客网

这一题也有意思

二叉树的层序遍历

判断是否为完全二叉树

二叉树的销毁就是走一个后续遍历

4.二叉树链式结构及实现

DFS :深度优先遍历（一般用递归）   ：走到无路可走就往回退（最经典为前序遍历）（三种序列都是深度优先遍历  但是要看有没有严格要求什么时候访问节点）

BFS：广度优先遍历（一般用队列） ：对于二叉树就是层序遍历（针对二叉树）