#1.一般线性回归
#方法思路:普通最小二乘法,平方误差最小化
#测试数据:
x = [[0,0],[1,1],[2,2]]
#将列表格式数据转为数组格式
x_1 = np.array(x)
y = [0,1,2]
#定义线性回归模型:
model = linear_model.LinearRegression()
#模型训练:
model.fit(x,y)
#可视化展示:
plt.scatter(x_1[:,0],x_1[:,1],color = 'blue')
plt.show()
#模型系数:
model.coef_
print('模型系数为:',model.coef_)
#--------------示例2:---------------------
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
diabetes = datasets.load_diabetes()
#newaxis:将抽取的数据每个转换为一列
diabetes_x = diabetes.data[:,np.newaxis,2]
#将数据分为训练集与测试集:
diabetes_x_train = diabetes_x[:-20]
diabetes_x_test = diabetes_x[-20:]
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]
#建立回归模型:
model = linear_model.LinearRegression()
#模型训练过程:
model.fit(diabetes_x_train, diabetes_y_train)
#进行数据预测:
diabetes_pred = model.predict(diabetes_x_test)
#模型误差分析:
error = mean_squared_error(diabetes_y_test, diabetes_pred)
r2_score = r2_score(diabetes_y_test, diabetes_pred)
#训练后的系数:
print('系数为:',model.coef_)
print('误差为:',error)
print('拟合度为:',r2_score)
#可视化展示:
plt.scatter(diabetes_x_test, diabetes_y_test, color = 'black')
plt.plot(diabetes_x_test, diabetes_pred, color = 'blue', linewidth = 3)
#去掉x轴坐标;
plt.xticks(())
#去掉y轴坐标:
plt.yticks(())
plt.show()
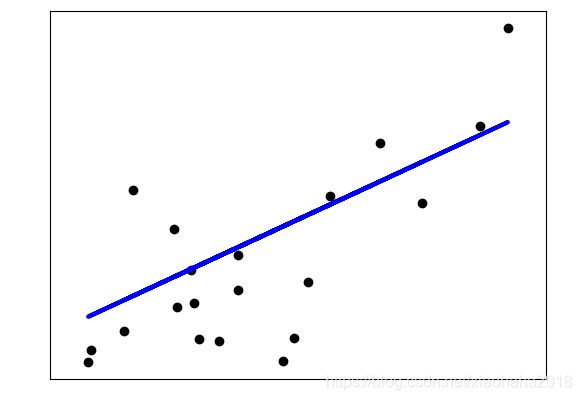





 博客主要介绍一般线性回归,采用普通最小二乘法使平方误差最小化。给出两个示例,包括将列表数据转为数组、定义线性回归模型、模型训练、可视化展示、系数计算、误差分析等操作,还进行了数据预测和拟合度评估。
博客主要介绍一般线性回归,采用普通最小二乘法使平方误差最小化。给出两个示例,包括将列表数据转为数组、定义线性回归模型、模型训练、可视化展示、系数计算、误差分析等操作,还进行了数据预测和拟合度评估。
















 8173
8173

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








