从数学角度分析为什么要戴口罩

很多人不重视不愿意戴口罩，主要是因为他们觉得自己离感染还很远，着是小概率事件。但是，聪明的你却可以通过数学告诉他们：虽然现在是小概率事件，但是要是他们不戴口罩和采取其他控制措施的话。马上就要演变成大概率时间。

具体来说，我们用到的是经典的SIR传染病模型：

SIR Model

其中N为总人口，S为未被感染的人，I为已经被感染的人，R为被治愈的人。

上面三个微分方程假设：

\1. 感染速度正比于总人口，2. 治愈率保持不变。3. 治愈了不会再发病

我们可以用现在的公开数据来模拟一下：

武汉一共有1000万人，假设1/10 100万人有机会接触到冠状病毒，12月8日第一个发病者发病，至今约45天。

我们可以根据公开数据大致算出上述模型的参数：

Beta（感染率/天）=0.00000015

gamma（治愈率/天）= 0.0077266

然后依据以上信息，可以随手写个代码：

R Code

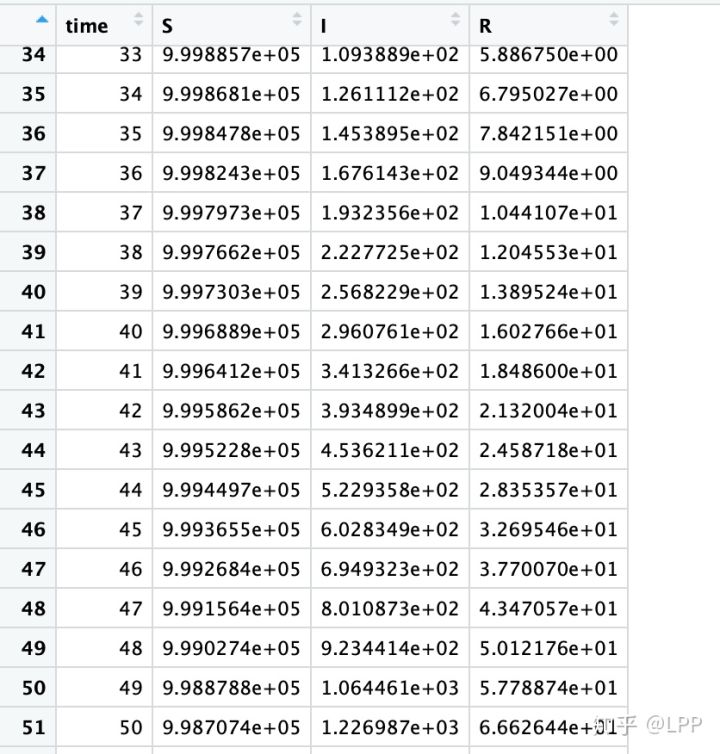S: 未感染人数； I：感染人数 R：治愈人数

我们可以看到第四十五天的时候，程序预测的：感染人数为602，治愈人数为32。和真实数据：确诊644，治愈30还是十分接近的。

然而可怕之处在哪里呢？如果我们现在什么都不做（不戴口罩也不限制出行），那么感染人数会成指数级上升，具体来说：

\1. 第50天感染超过1,000人

\2. 第65天超过10,000人

\3. 82天（3月1日）超过100,000人

\4. 第100天（3月29日）武汉一半的人都感染肺炎

5.第124天（4月12日）达到峰值全武汉79%的人都感染

画个图：

感染人口占总人口比率随时间变化图

我们可以看到70天以前，比率都在1%以内，然而一过70天，比率开始飞速增长到总人口的80%。这样你还觉得是小概率事件吗？可能你说，那我又不在武汉我不怕。可你要这样想啊：武汉12月8日也就只有一个人得病啊，假设今天你城市来了一个病人，那么你的今天难道不是12月8日的武汉吗？？这样你还会觉得离你生活很远吗？

那么戴口罩有什么用呢？

从数学上讲，戴口罩可以显著减少Beta（感染率/天），假设我们戴口罩可以让上面的beta减少y一半的值（变成0.000000075）。那么120天后，感染人数只有不戴口罩的1/100。

并且现实中，口罩的作用还能是使beta（感染率）的值减少一半还多（可能能减少到1/10），那样疫情就变得非常可控了。

所以明白了吗？一定要带口罩！

---

注：上面模型还没有考虑病人的死亡。假设有2.5%的死亡率，都会有2万5千人去世。所以现实情况远远比模型假设的要恐怖。

转载自: https://zhuanlan.zhihu.com/p/103890822

虽说无须指明出处，还是指明一下。

所以还是那句：别以为离你很远，要戴口罩。

答案是戴口罩。。。。