例:
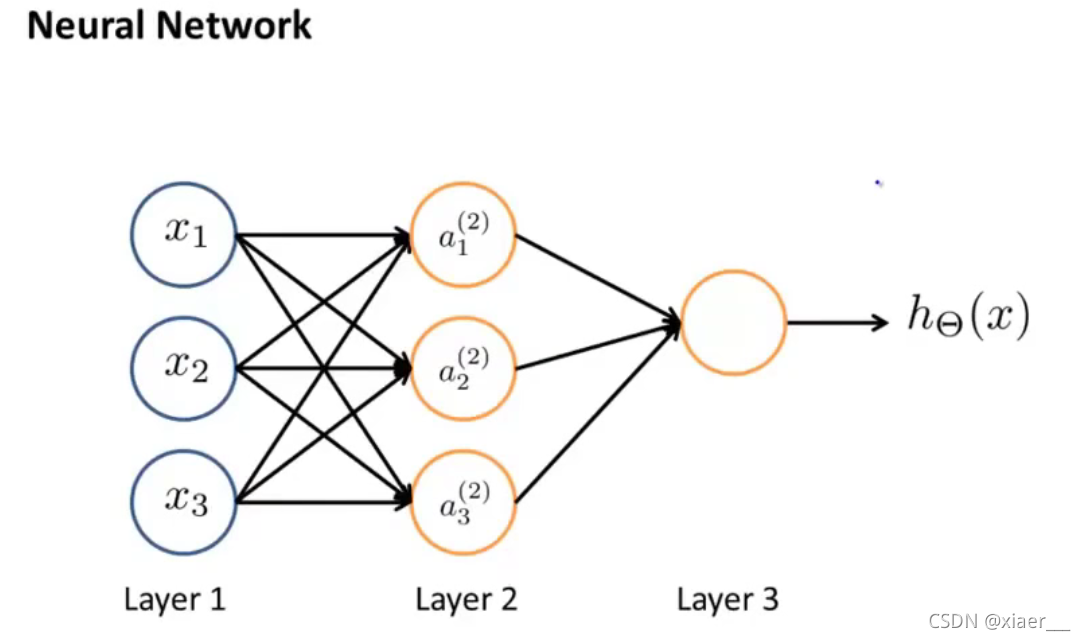
从左到右为输入层(1)、隐藏层(2)、输出层(3),(在整个神经网络中我们还会用到偏置值bias),其中隐藏层可以有多个
算法原理
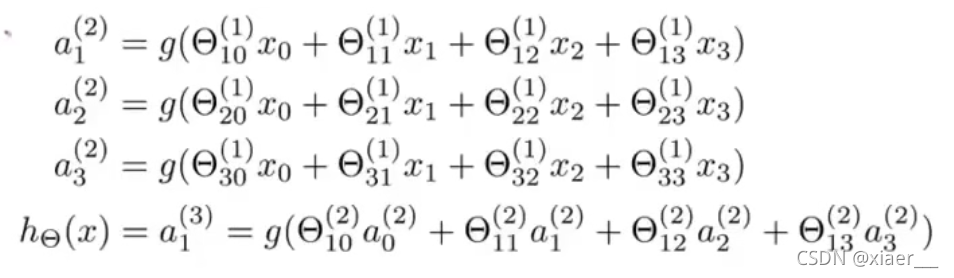
其中上标为层数,下标为该层中的某一个神经元,我们
将公式中的用
替代;
将公式中的用
替代;
将公式中的用
替代;
这样,我们就可以将计算进行向量化:
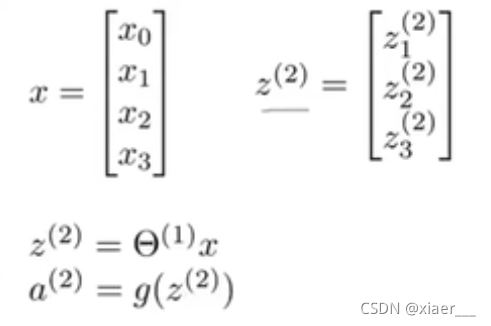
其中z是一个三维向量
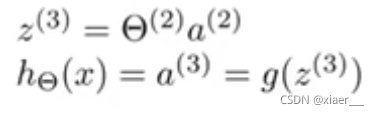
其中考虑到偏置值后,![]() ,加上偏置值,a成为了一个四维向量。其中g为激活函数,通过向量计算得到输出h
,加上偏置值,a成为了一个四维向量。其中g为激活函数,通过向量计算得到输出h
简单的神经网络使用示例
x1与x2的逻辑运算
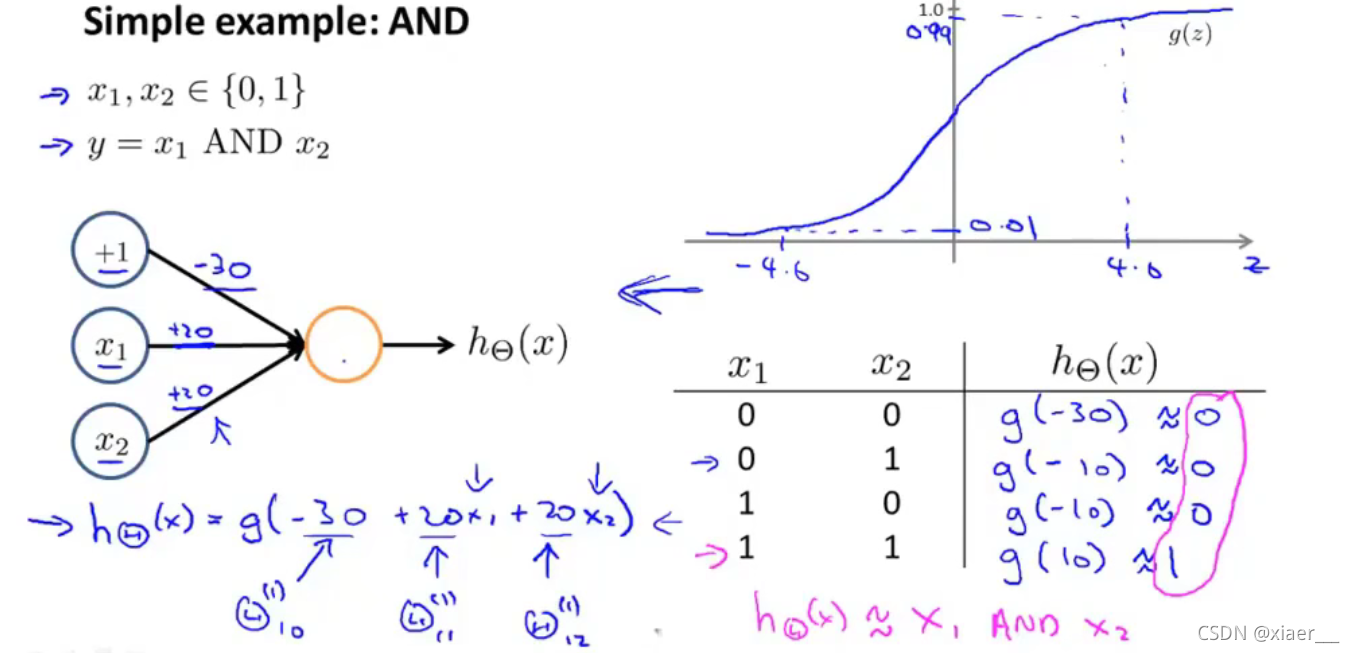
可以通过多层隐藏层来做更为复杂的运算
代价函数
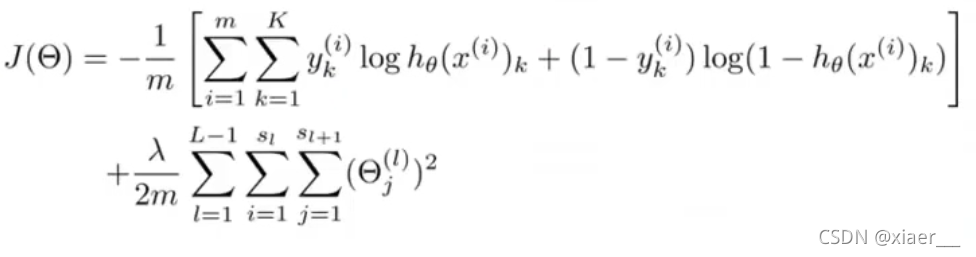
反向传播算法
基于代价函数,定义表示第i层第j个神经元的误差,
对于输出层的神经元: =
而对于隐藏层的神经元:
此算法,将输出层的误差,依次往后传播,直到第二层(没有第一层
,因为第一层是输入层,是数据来源,没有误差),故名反向传播算法
然后:
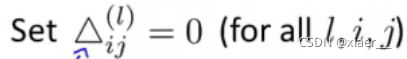
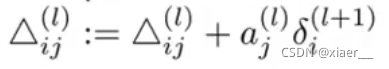
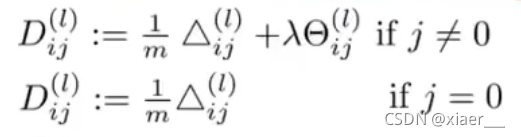
最后计算出的结果D即为损失函数J的偏导数
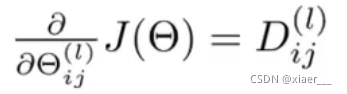





















 7581
7581

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








