Daily AI 20251217 (PyTorch基础回顾2)

CNN

• 输入图像：网络接收的原始图像数据。
• 卷积（Convolution）：使用卷积核（Kernel）在输入图像上滑动，提取特征，生成特征图（Feature Maps）。
• 池化（Pooling）：通常在卷积层之后，通过最大池化或平均池化减少特征图的尺寸，同时保留重要特征，生成池化特征图（Pooled Feature Maps）。
• 特征提取（Feature Extraction）：通过多个卷积和池化层的组合，逐步提取图像的高级特征。
• 展平层（Flatten Layer）：将多维的特征图转换为一维向量，以便输入到全连接层。
• 全连接层（Fully Connected Layer）：类似于传统的神经网络层，用于将提取的特征映射到输出类别。
• 分类（Classification）：网络的输出层，根据全连接层的输出进行分类。
• 概率分布（Probabilistic Distribution）：输出层给出每个类别的概率，表示输入图像属于各个类别的可能性。

输入层-卷积层-非线性激活-池化-归一化层-全连接（将提取的特征图展平为一维向量）-输出层

Normalization Layer and Batch Normalization (BN)

随着网络层数的加深，参数不断更新，每一层输入数据的分布（均值、方差）都在不断剧烈变化。会导致：

• 训练慢：后一层网络必须不断“适应”前一层传来的新分布，导致学习率必须设得很小。
• 梯度消失/爆炸：如果数据分布跑到了激活函数（如Sigmoid/Tanh）的饱和区，梯度会趋近于0，导致网络无法训练；即使是ReLU，数据分布过大也会导致权重更新不稳定。
• 对初始化敏感：如果初始权重没随机好，网络很容易崩。

归一化的作用就是：强行把每一层的输入拉回到一个标准的分布（通常是均值为0，方差为1），让网络在一个稳定的“舒适区”里训练。

能使用大batch_size训练时，适合用Batch Normalization；
当batch_size很小时，适合用Group Normalization；
做 NLP (Transformer)，适合用Layer Normalization；
做风格迁移/生成图像，适合用 Instance Normalization。

Batch Normalization (BN) 的数学原理

$\text{在 CNN 中，BN 的核心特征是：Channel－wise（按通道独立计算）}$
$\text{它在 Batch 维度（N）和空间维度（ H, W ）上进行聚合，为每一个通道 c 计算一组统计量。}$

设 CNN 某一层的输入张量为 $X$ ，输出张量为 $Y$ 。它们的形状均为 $(N,C,H,W)$ ，其中：

• $N$ ：Batch Size（批量大小）
• $C$ ：Channels（通道数／特征图数量）
• $H,W$ ：Height，Width（特征图的高和宽）

使用索引 $(n,c,h,w)$ 来定位张量中的某一个元素值 $x_{n,c,h,w}$ 。
－ n ∈ { 1 , … , N } n \in\{1, \ldots, N\} n∈{1,…,N}
－ c ∈ { 1 , … , C } c \in\{1, \ldots, C\} c∈{1,…,C}
－ h ∈ { 1 , … , H } h \in\{1, \ldots, H\} h∈{1,…,H}
－ w ∈ { 1 , … , W } w \in\{1, \ldots, W\} w∈{1,…,W}

若在一个卷积层之后、激活函数之前插入BN层：

• 对于每一个通道c，计算 batch中所有图像的 对应的通道c中 所有像素值的均值；集合 ${\mathcal{B}}_c$ 包含的元素个数为 $m=N\times H\times W$ 。
• 计算通道均值与方差：在 $(N,H,W)$ 三个维度上求均值与方差：
  $$\begin{gathered} {\mu }_c=\frac{1}{N\cdot H\cdot W}\sum _{n=1}^N\sum _{h=1}^H\sum _{w=1}^W{x}_{n,c,h,w} \\ {\sigma }_c^2=\frac{1}{N\cdot H\cdot W}\sum _{n=1}^N\sum _{h=1}^H\sum _{w=1}^W{\left(x_{n,c,h,w}-{\mu }_c\right)}^2 \end{gathered}$$
• 归一化：对该通道内的每一个元素进行标准化，使其服从 $N(0,1)$ 分布。
  $${\hat{x}}_{n,c,h,w}=\frac{x_{n,c,h,w}-{\mu }_c}{\sqrt{{\sigma }_c^2+ϵ}}$$
• 缩放与平移：引入可学习的参数 ${\gamma }_c$ 和 ${\beta }_c$ 。注意，$\gamma$ 和 $\beta$ 是向量，长度为 $C$ ，即每个通道拥有自己独特的一对 ${\gamma }_c,{\beta }_c$ 。
  $$y_{n,c,h,w}={\gamma }_c\cdot {\hat{x}}_{n,c,h,w}+{\beta }_c$$
• 参数数量：因为有 $C$ 个通道，所以最终网络需要学习 $C$ 个 $\gamma$ 值 和 $C$ 个 $\beta$ 值，以及在推理阶段使用的 $C$ 个全局 running＿mean 和 $C$ 个全局 running＿var 。

Batch Normalization (BN) 训练与推理

训练时

• 使用当前Mini－batch的均值 ${\mu }_{\mathcal{B}}$ 和方差 ${\sigma }_{\mathcal{B}}^2$ 进行归一化。
• 同时，BN层会维护一对全局统计量（Global Statistics）：running＿mean 和 running＿var。它们通过移动平均（Moving Average）的方式不断更新，记录整个数据集的分布特征。
  $$\text{ running-mean }=(1-\text{ momentum })\times \text{ running-mean }+\text{ momentum }\times {\mu }_{\mathcal{B}}$$

推理时

• 直接使用训练期间计算好的 running＿mean 和 running＿var 以及学习到的 $\gamma ,\beta$ 来处理数据。

Batch Normalization (BN) 实现

import torch
import torch.nn as nn

# 假设输入是一个 mini-batch: N=2, C=3, H=2, W=2
input_tensor = torch.randn(2, 3, 2, 2)

# 定义 BN 层，num_features 必须等于输入的通道数 C
# track_running_stats=True 表示会追踪全局均值和方差用于推理
bn_layer = nn.BatchNorm2d(num_features=3, affine=True, track_running_stats=True)

# --- 训练阶段 ---
bn_layer.train() # 开启训练模式
output = bn_layer(input_tensor)

print("Scale (gamma):", bn_layer.weight.data) # 初始通常为全1
print("Shift (beta):", bn_layer.bias.data)    # 初始通常为全0
print("Running Mean:", bn_layer.running_mean) # 初始为0，随训练更新
print("Running Var:", bn_layer.running_var)   # 初始为1，随训练更新

# --- 推理阶段 ---
bn_layer.eval() # 开启评估模式
# 此时 forward 过程不再计算 batch 均值，而是用 running_mean/var
test_output = bn_layer(input_tensor)

Layer Normalization

对每一个样本的所有通道和空间信息进行归一化。
对于输入维度(N-C-H-W)；对于单个样本（此处是单个图片），在(C-H-W)维度上聚合：

• 对于第 $n$ 个样本，计算均值：
  $${\mu }_n=\frac{1}{C\cdot H\cdot W}\sum _{c=1}^C\sum _{h=1}^H\sum _{w=1}^W{x}_{n,c,h,w}$$
• 计算方差
  $${\sigma }_n^2=\frac{1}{C\cdot H\cdot W}\sum _{c=1}^C\sum _{h=1}^H\sum _{w=1}^W{\left(x_{n,c,h,w}-{\mu }_n\right)}^2$$
• 归一化 （这里的 ${\mu }_n$ 和 ${\sigma }_n$ 对同一个样本内的所有 $C$ 个通道都是一样的）
  $${\hat{x}}_{n,c,h,w}=\frac{x_{n,c,h,w}-{\mu }_n}{\sqrt{{\sigma }_n^2+ϵ}}$$
• 缩放与平移
  $$y_{n,c,h,w}={\gamma }_c\cdot {\hat{x}}_{n,c,h,w}+{\beta }_c$$

Group Normalization

GN 是 LN 和 IN 的折中方案，为解决 BN 在小 Batch Size 下性能崩塌的问题。

由于CNN 的通道特征通常不是完全独立的，而是分组的（例如，一组通道提取形状，另一组提取纹理）。GN 顺应了这种“群组特征”。

• 预处理：将通道数 $C$ 分成 $G$ 个组，每组包含 $M=C/G$ 个通道。需要计算当前通道 $c$ 属于哪一个组，记组索引为 $g_c=\lfloor \frac{c}{M}\rfloor$ 。
• 计算范围：对于固定的样本 $n$ 和固定的组 $g$ ，在 $(M,H,W)$ 维度上聚合。即＂一部分通道＋所有空间像素＂。
• 计算均值 对于第 $n$ 个样本的第 $g$ 个组（该组包含的通道集合记为 ${\mathcal{C}}_g$ ）：
  $${\mu }_{n,g}=\frac{1}{M\cdot H\cdot W}\sum _{c\in {\mathcal{C}}_g}\sum _{h=1}^H\sum _{w=1}^W{x}_{n,c,h,w}$$
• 计算方差
  $${\sigma }_{n,g}^2=\frac{1}{M\cdot H\cdot W}\sum _{c\in {\mathcal{C}}_g}\sum _{h=1}^H\sum _{w=1}^W{\left(x_{n,c,h,w}-{\mu }_{n,g}\right)}^2$$
• 归一化（同一个 Group 内的所有通道共用这一个均值和方差）
  $${\hat{x}}_{n,c,h,w}=\frac{x_{n,c,h,w}-{\mu }_{n,g}}{\sqrt{{\sigma }_{n,g}^2+ϵ}}$$
• 缩放平移（$\gamma$ 和 $\beta$ 依然是 Channel－wise 的，每个通道都有自己独立的缩放参数）
  $$y_{n,c,h,w}={\gamma }_c\cdot {\hat{x}}_{n,c,h,w}+{\beta }_c$$

Instance Normalization

把每个样本的每个通道都看作独立的个体；对于固定的样本 $n$ 和固定的通道 $c$，我们只在 $(H,W)$ 空间维度上聚合

为什么 Transformer 需要用 LN 而不是 BN

CNN由于平移不变性（如果在图片的左上角检测到了“边缘”，和在右下角检测到“边缘”，它们应该被同等对待），因此，对于batch所有样本的同一个通道$c$，无论像素在哪个位置 $(h,w)$，都希望用同一组缩放系数 $({\gamma }_c,{\beta }_c)$ 来调整它。

对于NLP-Transformer，输入形状 (batch_size N - sequence length L - embedding dimension D)；需针对 Embedding 向量的每一个元素（Element）都有独立的参数。

• 计算均值：针对第 $n$ 个句子的第 $l$ 个单词，计算其 $D$ 个特征值的平均值：
  $${\mu }_{n,l}=\frac{1}{D}\sum _{d=1}^D{x}_{n,l,d}$$
  结果 ${\mu }_{n,l}$ 是一个标量，它只与当前单词有关，不依赖其他单词，也不依赖 Batch里的其他句子。
• 计算方差
  $${\sigma }_{n,l}^2=\frac{1}{D}\sum _{d=1}^D{\left(x_{n,l,d}-{\mu }_{n,l}\right)}^2$$
• 归一化：对该单词向量的每一个特征 $d$ 进行标准化：
  $${\hat{x}}_{n,l,d}=\frac{x_{n,l,d}-{\mu }_{n,l}}{\sqrt{{\sigma }_{n,l}^2+ϵ}}$$
• 缩放与平移：使用可学习参数 $\gamma$ 和 $\beta$ 进行仿射变换。
  $$y_{n,l,d}={\gamma }_d\cdot {\hat{x}}_{n,l,d}+{\beta }_d,\forall d=0,\cdots ,D-1$$

• 不定长序列与 Padding 问题
  BN的逻辑：BN 需要在 Batch 维度上求均值。而NLP 一个 Batch 里的句子长度不一样，句子 A 有 5 个词，句子 B 有 100 个词。为了凑成 Tensor，短句子必须补 0 。
  如果用 BN，那些大量的Padding 0 会被算进均值和方差里，导致统计量严重偏移，不仅本身算不准，还会把这种偏差＂污染＂给长句子中的有效词。
  LN 只算当前这个单词自己的 $D$ 维向量的均值方差，句子长短、Padding 多少，完全不影响当前这个有效单词的归一化计算。
• Training 与 Inference 的一致性
  在 Transformer-GPT中，推理是自回归的。需通过 $t$ 时刻生成的词，去预测 $t+1$ 时刻。如果使用 BN，推理时需要一个全局统计量。但在 NLP 中，不同长度、不同语义的句子统计特性差异巨大，很难用一个全局统计量概括所有句子的分布。
• Batch Size 的限制
  Transformer 模型通显存占用高。导致训练时的 Batch Size 往往很小；当 Batch Size 很小时，BN 的统计量极其不稳定，会导致模型无法收敛。

默写CNN-MNIST–版本1：

# 导入库
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

from torchvision import datasets, transforms

# import matplotlib.pyplot as plt

'数据加载与预处理'
# data processing
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5,), (0.5,))
                                ])

train_dataset = datasets.MNIST(root='.\data\mnist',
                               train=True, transform=transform, download=False)
test_dataset = datasets.MNIST(root='.\data\mnist',
                              train=False, transform=transform, download=False)

# data loading
train_loader = torch.utils.data.DataLoader(
    dataset=train_dataset, batch_size=32, shuffle=True)

test_loader = torch.utils.data.DataLoader(
    dataset=test_dataset, batch_size=32, shuffle=False)


'模型构建'
class simpleCNN(nn.Module):

    _n_cls = 10

    def __init__(self):
        # py3 特性 自动继承父类
        super().__init__()
        self.conv1 = nn.Conv2d(1, 32, kernel_size=3, stride=1, padding=1)
        self.pooling1 = nn.MaxPool2d(kernel_size=2)
        self.conv2 = nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1)
        self.pooling2 = nn.MaxPool2d(kernel_size=2)
        self.linear1 = nn.Linear(64*7*7, 256)
        self.linear2 = nn.Linear(256, self._n_cls)

    def forward(self, x):

        x = self.conv1(x)
        x = F.relu(x)
        x = self.pooling1(x)
        x = self.conv2(x)
        x = F.relu(x)
        x = self.pooling2(x)
        x = x.view(-1, 64*7*7)
        x = self.linear1(x)
        x = F.relu(x)
        x = self.linear2(x)

        return x

# model initialization
model = simpleCNN()
model.train()

# 定义损失函数与优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=1e-2, momentum=0)

# 训练模型
acc_lis = []
epoch = 5
for ep in range(epoch):
    total_loss = 0
    # count = 0
    for idx, (img, lab) in enumerate(train_loader):

        # forward to generate
        out = model(img)
        loss = criterion(out, lab)
        loss.backward()
        optimizer.step()
        total_loss += loss.item()

        # count += 1
        # if count >= 10:
        #     break

    model.eval()
    correct = 0
    total = 0
    with torch.no_grad():
        for img, lab in test_loader:
            test_out = model(img)
            _, predicted = torch.max(test_out, 1)
            total += lab.size(0)
            correct += (predicted == lab).sum().item()

    acc = 100 * correct / total
    acc_lis.append(acc)
    print(f'round: {ep}, test accuracy = {acc}%')

Hints 1

nn.Conv2d()

self.conv1 = nn.Conv2d(in_channels=1, out_channels=32, kernel_size=3, stride=1, padding=1)

in_channels (输入通道数): （MNIST灰度图 故是1）
out_channels (输出通道数）
kernel_size (卷积核大小)：滑动窗口的大小
stride (步长)：卷积核每次滑动的距离
padding (填充)：在输入图像周围填充 0 的圈数

nn.MaxPool2d()

用于下采样，减少计算量，并提取最显著的特征（即最大值）

self.pooling1 = nn.MaxPool2d(kernel_size=2, stride=2)

kernel_size: 池化窗口的大小

• 在 MaxPool 中，如果不指定 stride，默认值等于 kernel_size。这意味着窗口之间不重叠。
• $2\times 2$ 的池化会让图像的长和宽直接减半

nn.Linear()

用于将提取出的特征矩阵展平并进行分类。

self.linear1 = nn.Linear(in_features=64*7*7, out_features=256)

• in_features: 输入向量的长度，须与上一层输出并Flatten后的元素总数严格匹配。
• out_features: 输出向量的长度。

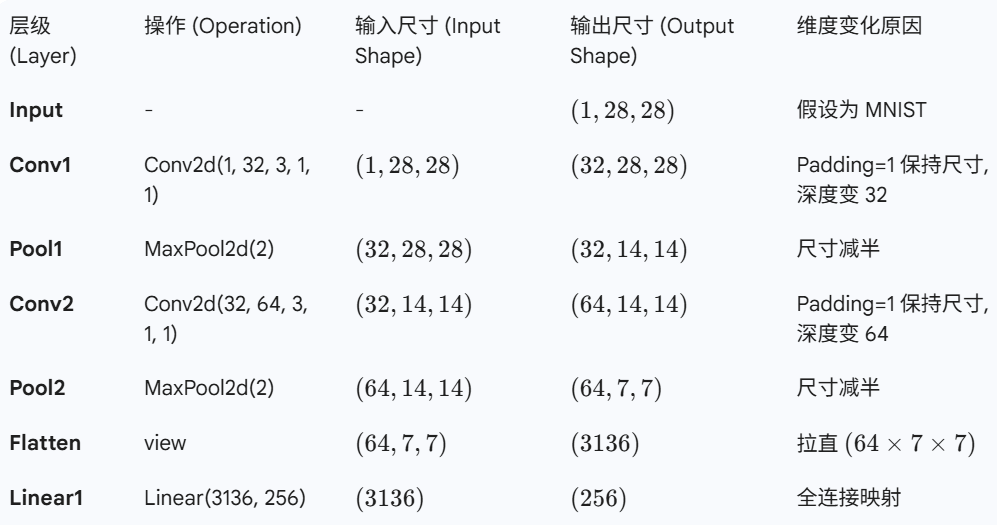
维度推演

初始输入
－形状：（1，28，28）
1．self．conv1（x）

• 参数：$K=3,S=1,P=1$
• 计算：$H_{\text{out }}=\frac{28-3+2\times 1}{1}+1=28$
• 通道数变为了 out＿channels＝32。
• 输出形状：$(32,28,28)$

2．self．pooling1（ x ）

• 参数：$K=2$ ，默认 $S=2$
• 计算：$H_{\text{out }}=\frac{28}{2}=14$
• 通道数不变。
• 输出形状：（ $32,14,14$ ）

3．self．conv2（x）

• 输入通道必须是 32 （匹配上一层）。
• 参数：$K=3,S=1,P=1$（注意这里又是 Padding＝1，Stride＝1，所以长宽不变）
• 计算：$H_{\text{out }}=\frac{14-3+2\times 1}{1}+1=14$
• 通道数变为了 out＿channels $=64$ 。
• 输出形状：（ $64,14,14$ ）

4．self．pooling2（x）

• 参数：$K=2,S=2$
• 计算：$H_{\text{out }}=\frac{14}{2}=7$
• 通道数不变。
• 输出形状：（ $64,7,7$ ）

5．$x.\mathrm{view}(-1,64\ast 7\ast 7)$

• 这里是卷积层到全连接层的过渡。
• 此时的数据形状是（Batch，64，7，7），是一个三维的立方体数据。
• 全连接层只接受一维向量（除了 Batch 维）。
• 需要把 64 个 $7\times 7$ 的特征图全部拉直。
• 总元素数量 $=64\times 7\times 7=3136$ 。

维度匹配

对于卷积层，输出尺寸 $O$ 的计算公式为：
$$O=\frac{I-K+2P}{S}+1$$
其中：$I=$ 输入尺寸，$K=$ 卷积核大小，$P=$ Padding，$S=$ Stride。

当 $kernel\_size=3$ 且 $stride=1$ 时，设置 $padding=1$
可以保持输入和输出的长宽尺寸不变（只有深度变了）
代入公式：O = ( I - 3 + 2*1 ) / 1 + 1 = I

x.view(-1, 6477)

由于x目前的形状为：$$(\text{Batch\_Size},\text{Channel},\text{Height},\text{Width})$$
-1: 代表 “自动计算未知的维度”，PyTorch 会根据元素总数保持不变的原则，自动计算这一维应该是多少，此处，-1 就会自动变成 Batch_Size：$$(Batch\_Size,3136)$$

• .view() 的用法与机制
  $$\begin{gathered} 核心规则：元素总数必须守恒 \\ 变换前的形状乘积，必须等于变换后的形状乘积。 \end{gathered}$$

• 具体示例

x = torch.zeros([2,3,4])

x1 = x.view(-1,24)
'torch.Size([1, 24])'   

# 我想要变成 1 行，长度自动算
x2 = x.view(-1)
'torch.Size([24])'

# 我想要保持第0维(2)不变，后面全部拉直
x3 = x.view(2, -1)
'torch.Size([2, 12])'

# 我想要变成 (4, 6) 的形状
x4 = x.view(4, 6)
'torch.Size([4, 6])'

print(x1.size(),x2.size(),x3.size(),x4.size())

• view(): 要求数据在内存中是连续的 (Contiguous)。如果之前对张量做过 transpose 或 permute（转置/换位）操作，数据在内存里的顺序就乱了，直接用 view 会报错。
• 解决方法: x.contiguous().view(…)
• reshape(): 如果数据不连续，它会自动复制一份新的数据使其连续，然后再变形

Hints 2

model.eval()
    correct = 0
    total = 0
    with torch.no_grad():
        for img, lab in test_loader:
            test_out = model(img)
            # print(test_out)
            _, predicted = torch.max(test_out, 1)
            total += lab.size(0)
            correct += (predicted == lab).sum().item()

    acc = 100 * correct / total
    acc_lis.append(acc)
    print(f'round: {ep}, test accuracy = {acc}%')

model.eval()

Dropout 层在训练时会随机丢弃神经元，但在测试时必须停止丢弃；Batch Normalization 层在训练时使用当前 batch 的均值和方差，而在测试时使用全局统计的均值和方差。

with torch.no_grad():

创建一个上下文环境，在这个缩进块内的所有计算都不会计算梯度；测试阶段只需要前向传播，不需要反向传播，关闭梯度可以大幅提升速度。

for img, lab in test_loader:

从 test_loader 中逐个batch提取数据：32张图，每张图对应 0-9 共 10 个类别的分数）。分数越高的类别，代表模型认为越可能是该数字

img.size(): torch.Size([32, 1, 28, 28])
lab.size(): torch.Size([32])
lab: tensor([7, 2, 1, 0, 4, 1, 4, 9, 5, 9, 0, 6, 9, 0, 1, 5, 9, 7, 3, 4, 9, 6, 6, 5, 4, 0, 7, 4, 0, 1, 3, 1])

test_out = model(img)

输出batch_size个logits向量：

test_out.size(): torch.Size([32, 10])

_, predicted = torch.max(test_out, 1)

找出每张图中分数最高的那个类别的索引。

torch.max(tensor, dim)

torch.max(tensor, dim) 会返回两个值：第一个是最大值本身（用 _ 忽略），第二个是最大值的索引（即模型预测的数字）。

' _ 是一个惯用的占位符变量名，表示“不关心此返回值，后续也不会使用” '

参数 1 表示在第 1 维度（横向，即类别维度）上找最大值。

predicted 就是模型给出的最终答案，例如 [7, 2, 1, …]。

print(predicted)
'tensor([7, 2, 1, 0, 4, 1, 7, 4, 0, 7, 0, 0, 4, 0, 1, 3, 7, 7, 3, 4, 8, 6, 6, 5, 4, 0, 7, 4, 0, 1, 3, 1])'

total += lab.size(0)

累加这一批次的样本数量

lab.size()
'''
返回值：torch.Size 对象: torch.Size([32])
'''

correct += (predicted == lab).sum().item()

• predicted == lab：逐元素比较，生成一个布尔张量（例如 [True, False, True, …]）。
• .sum()：将布尔值求和（True 为 1，False 为 0），得到这一批次猜对的个数（例如 tensor(28)）。
• .item()：将 PyTorch 的 0 维张量（Tensor）转换为标准的 Python 数字（int/float）。如果不加 .item()，累加的将是 Tensor 对象，会导致显存泄露。.item()只适用于包含一个元素的Tensor

'''
当对 Tensor 进行运算（如 sum()）时，PyTorch 会默认构建计算图以便进行反向传播。生成的 Tensor 即使只是一个标量，其也可能挂载 grad_fn

加上 .item()： 把 Tensor 里的数值取出来，变成一个普通的 Python 数字，不包含梯度信息，从而切断了计算图，释放显存，防止多轮训练出现显存溢出
'''

tensor维度定义

$Tensor的维度（从左到右，Dim0,Dim\mathrm{1...}）代表了从宏观到微观的“层级”。$

对于4D [B, C, H, W]
Dim 0 ( B ): Batch Size 图索引
Dim 1 ( C ): Channels 颜色通道（RGB）。
Dim 2 ( H ): Height 图片高
Dim 3 ( W ): Width 图片宽

可视化代码（Gemini）：

import torch
import matplotlib.pyplot as plt
import numpy as np

def visualize_4d_tensor():
    # 1. 定义维度参数
    B, C, H, W = 4, 3, 32, 32
    # Batch=4 (4张图)
    # Channel=3 (RGB 3通道)
    # Height=32, Width=32 (像素大小)

    print(f"创建 4D Tensor，形状为: [{B}, {C}, {H}, {W}]")
    print("-" * 30)

    # 2. 创建模拟数据
    # 为了演示，我们生成随机噪音图
    tensor_4d = torch.rand(B, C, H, W)
    
    # 3. 可视化逻辑
    # 我们将展示每一张图（Dim 0），以及每一张图的每一个通道（Dim 1）
    
    fig, axes = plt.subplots(B, C + 1, figsize=(12, 10))
    # 每一行代表一个 Batch (Dim 0)
    # 前三列代表 R, G, B 通道 (Dim 1)
    # 最后一列代表 合成的彩色图

    for b in range(B): # 遍历 Dim 0 (批次)
        
        # --- 拿出一张完整的图 ---
        single_img_tensor = tensor_4d[b] # 形状变成 [3, 32, 32]
        
        # 这里的技巧：Matplotlib 需要 [H, W, C] 格式，而 PyTorch 是 [C, H, W]
        # 所以我们需要 .permute(1, 2, 0) 交换维度
        img_for_plot = single_img_tensor.permute(1, 2, 0).numpy()
        
        # 显示合成图
        axes[b, C].imshow(img_for_plot)
        axes[b, C].set_title(f"Batch {b}\n(Full Color)", fontsize=10, color='red')
        axes[b, C].axis('off')
        
        # --- 遍历该图的 3 个通道 ---
        for c in range(C): # 遍历 Dim 1 (通道)
            
            # 取出单通道数据，形状 [32, 32]
            channel_img = tensor_4d[b, c, :, :] 
            
            # 显示灰度图（因为单通道本质就是灰度矩阵）
            axes[b, c].imshow(channel_img, cmap='gray')
            axes[b, c].set_title(f"Batch {b}\nChannel {c}", fontsize=10)
            axes[b, c].axis('off')

    plt.tight_layout()
    plt.show()

# 运行可视化
visualize_4d_tensor()