关于LCA（Tarjan+ST）

最新推荐文章于 2025-02-15 15:00:03 发布

原创最新推荐文章于 2025-02-15 15:00:03 发布 · 625 阅读

0 ·

CC 4.0 BY-SA版权

ACM_图论专栏收录该内容

19 篇文章

订阅专栏

本文深入讲解了Tarjan算法，一种解决最近公共祖先(LCA)问题的高效离线算法。通过结合深度优先遍历与并查集，实现了线性的处理时间。文章提供了详细的算法流程与示例代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

又是深夜更新博客。。。为的是写一下今天学的LCA（Least Common Ancestors），也就是最近祖先问题。。。最近祖先也就是离根结点最远的祖先。。。

有两种算法，一种是离线算法：Tarjan算法（突然觉得这个人提出了好多算法。。。），第二种是在线算法：ST算法。

由于今天只看了Tarjan算法、它的一些拓展和RMQ，并没有写ST的模板，再加上没有数据结构的基础。。到现在还不能透彻地了解树、二叉树和各种什么什么的二叉树

这里先贴一下大神的链接，http://dongxicheng.org/structure/lca-rmq/（后面的算法介绍也就用大神的了/。。）接下去先写关于Tarjan算法。。（其实我觉得Tarjan算法更好一

点。。。）

Tarjan

所谓离线算法，是指首先读入所有的询问（求一次LCA叫做一次询问），然后重新组织查询处理顺序以便得到更高效的处理方法。Tarjan算法是一个常见的用于解决LCA问题的离线算法，它结合了深度优先遍历和并查集，整个算法为线性处理时间。

Tarjan算法是基于并查集的，利用并查集优越的时空复杂度，可以实现LCA问题的O(n+Q)算法，这里Q表示询问的次数。更多关于并查集的资料，可阅读这篇文章：《数据结构之并查集》。

同上一个算法一样，Tarjan算法也要用到深度优先搜索，算法大体流程如下：对于新搜索到的一个结点，首先创建由这个结点构成的集合，再对当前结点的每一个子树进行搜索，每搜索完一棵子树，则可确定子树内的LCA询问都已解决。其他的LCA询问的结果必然在这个子树之外，这时把子树所形成的集合与当前结点的集合合并，并将当前结点设为这个集合的祖先。之后继续搜索下一棵子树，直到当前结点的所有子树搜索完。这时把当前结点也设为已被检查过的，同时可以处理有关当前结点的LCA询问，如果有一个从当前结点到结点v的询问，且v已被检查过，则由于进行的是深度优先搜索，当前结点与v的最近公共祖先一定还没有被检查，而这个最近公共祖先的包涵v的子树一定已经搜索过了，那么这个最近公共祖先一定是v所在集合的祖先。

【举例说明】

根据实现算法可以看出，只有当某一棵子树全部遍历处理完成后，才将该子树的根节点标记为黑色（初始化是白色），假设程序按上面的树形结构进行遍历，首先从节点1开始，然后递归处理根为2的子树，当子树2处理完毕后，节点2， 5， 6均为黑色；接着要回溯处理3子树，首先被染黑的是节点7（因为节点7作为叶子不用深搜，直接处理），接着节点7就会查看所有询问(7, x)的节点对，假如存在(7, 5)，因为节点5已经被染黑，所以就可以断定(7, 5)的最近公共祖先就是find(5).ancestor，即节点1（因为2子树处理完毕后，子树2和节点1进行了union，find(5)返回了合并后的树的根1，此时树根的ancestor的值就是1）。有人会问如果没有(7, 5)，而是有(5, 7)询问对怎么处理呢? 我们可以在程序初始化的时候做个技巧，将询问对(a, b)和(b, a)全部存储，这样就能保证完整性。

我觉得上面的文字写的真是太赞了！下面的模板代码是我自己写的

/***************************************************************************************************
查询过程始终是框定在某一棵子树里面的，所以只有两种情况：1.另外一点没有被遍历过，

那么等待下次回溯的时候回溯到要查询的另外一点2.另外一点已经被遍历过，那么就输出

另外一点的祖先节点，而这个祖先节点必定为他们两者的最近祖先节点（原因很简单，这

是dfs，对于这个祖先节点，必然先遍历完它的左子树再遍历它的右子树，此时他的左子树

的所有点都会存有这个祖先节点
******************************************************************************************************/
#include <cstdio>
#include <string.h>
#include <vector>
using namespace std;
int const MAX = 10000;
vector<int> G[MAX];
int fa[MAX];
int vis[MAX];//判断某点是不是回溯到的，如果是回溯到的就进行查询操作
int n, q1, q2;

void init()
{
    for(int i = 1; i <= n; i++){
        vis[i] = 0;
        G[i].clear();
    }
}

int find(int x)//寻找祖先节点
{
    while(x != fa[x])
        x = fa[x];
    return x;
}

void tarjan(int u)
{
    vis[u] = 1;
    fa[u] = u;
    for(int i = 0; i < G[u].size(); i++){
        int v = G[u][i];
        if(!vis[v]){
            tarjan(v);
            fa[v] = u;
        }
    }
    if(u == q1 || u == q2){//这里假设查询q1和q2两点
        if(u == q1 && vis[q2])
            ans = find(q2);
        else if(u == q2 && vis[q1])
            ans = find(q1);
    }
}

经典例题

http://poj.org/problem?id=1330

Nearest Common Ancestors

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 24999		Accepted: 12984

Description

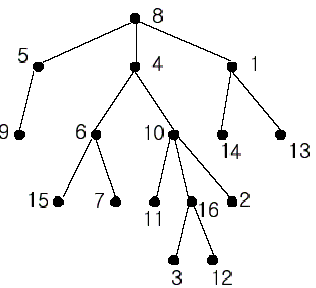
A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:

In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.

Write a program that finds the nearest common ancestor of two distinct nodes in a tree.

Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.

Output

Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.

Sample Input

Sample Output

4
3

这题唯一要注意的是：入度为0的根节点不确定，所以要用in数组来判断

#include <cstdio>
#include <vector>
#include <string.h>
using namespace std;
int const MAX = 10005;
vector<int> G[MAX];
int fa[MAX];
int in[MAX], vis[MAX];
int n;
int q1, q2, ans;
int find(int x)
{
    while(x != fa[x])
        x = fa[x];
    return x;
}

void tarjan(int u)
{
    vis[u] = 1;
    fa[u] = u;
    for(int i = 0; i < G[u].size(); i++){
        int v = G[u][i];
        if(!vis[v]){
            tarjan(v);
            fa[v] = u;
        }
    }
    if(u == q1 || u == q2){
        if(u == q1 && vis[q2])
            ans = find(q2);
        else if(u == q2 && vis[q1])
            ans = find(q1);
    }
}

int main()
{
    int cases;
    scanf("%d", &cases);
    while(cases--){
        memset(vis, 0, sizeof(vis));
        memset(in, 0, sizeof(in));
        scanf("%d", &n);
        for(int i = 1; i <= n; i++)
            G[i].clear();
        for(int i = 1; i < n; i++){
            int u, v;
            scanf("%d %d", &u, &v);
            in[v]++;
            G[u].push_back(v);
            G[v].push_back(u);
        }
        scanf("%d %d", &q1, &q2);
        for(int i = 1; i < n; i++){
            if(!in[i]){
                tarjan(i);
                break;
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

未完待续。。。