D. Sonya and Matrix

D. Sonya and Matrix

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Since Sonya has just learned the basics of matrices, she decided to play with them a little bit.

Sonya imagined a new type of matrices that she called rhombic matrices. These matrices have exactly one zero, while all other cells have the Manhattan distance to the cell containing the zero. The cells with equal numbers have the form of a rhombus, that is why Sonya called this type so.

The Manhattan distance between two cells ($x_1$, $y_1$) and ($x_2$, $y_2$) is defined as $|x_1-x_2|+|y_1-y_2|$. For example, the Manhattan distance between the cells $(5,2)$ and $(7,1)$ equals to $|5-7|+|2-1|=3$.

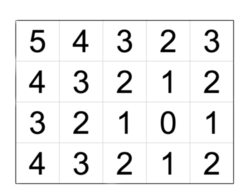Example of a rhombic matrix.

Note that rhombic matrices are uniquely defined by $n$, $m$, and the coordinates of the cell containing the zero.

She drew a $n\times m$ rhombic matrix. She believes that you can not recreate the matrix if she gives you only the elements of this matrix in some arbitrary order (i.e., the sequence of $n\cdot m$ numbers). Note that Sonya will not give you $n$ and $m$, so only the sequence of numbers in this matrix will be at your disposal.

Write a program that finds such an $n\times m$ rhombic matrix whose elements are the same as the elements in the sequence in some order.

Input

The first line contains a single integer $t$ ($1\le t\le {10}^6$) — the number of cells in the matrix.

The second line contains $t$ integers $a_1,a_2,\dots ,a_t$ ($0\le a_i<t$) — the values in the cells in arbitrary order.

Output

In the first line, print two positive integers $n$ and $m$ ($n\times m=t$) — the size of the matrix.

In the second line, print two integers $x$ and $y$ ($1\le x\le n$, $1\le y\le m$) — the row number and the column number where the cell with $0$ is located.

If there are multiple possible answers, print any of them. If there is no solution, print the single integer $-1$.

Examples

input

Copy

20
1 0 2 3 5 3 2 1 3 2 3 1 4 2 1 4 2 3 2 4

output

Copy

4 5
2 2

input

Copy

18
2 2 3 2 4 3 3 3 0 2 4 2 1 3 2 1 1 1

output

Copy

3 6
2 3

input

Copy

6
2 1 0 2 1 2

output

Copy

-1

Note

You can see the solution to the first example in the legend. You also can choose the cell $(2,2)$ for the cell where $0$ is located. You also can choose a $5\times 4$ matrix with zero at $(4,2)$.

In the second example, there is a $3\times 6$ matrix, where the zero is located at $(2,3)$ there.

In the third example, a solution does not exist.

思路：

    设 0的坐标为（x，y），矩阵的大小为（m，n），矩阵第一行第一列为（1，1）(在这里我们要把矩阵翻过来看）；设 a=x-1+y-1 , b=m-x +n-y;

则a表示0到（1，1）的距离，b表示0到m，n的距离，这里注意，很容易知道b的值就是输入数中最大的那一个，因为最大的那个数距离0是最远的。

将a=x-1+y-1 , b=m-x +n-y合并得 a=m+n-2-b;代入a=x-1+y-1中得到y=n+m-b-x; 如果 a[i] != 4*i,x=i;

代码：

#include<bits/stdc++.h>

 using namespace std;
 const int N=1e6+10;
 int a[N],d[N];
 int t;
 int n,m;
 int x,y;
 int b;///矩阵角落到"0"的最大距离
 ///y=n+m-b-x
 int main()
 {
     while(scanf("%d",&t)!=EOF){
         memset(a,0,sizeof(a));
         b=0;
         for(int i=1;i<=t;i++){
             int num;
             scanf("%d",&num);
             a[num]++; //这样a[i]=n 就代表数i有n个
             b=max(b,num);//找最大的那个数
         }
         x=1;///x需要初始化为1,因为x的最小值为1，我们可能在下面的循环中，找不到这样的x
             ///从而导致x的值不确定.eg:1 0这一组数据。
         for(int i=1;i<b;i++)
         if(a[i]!=4*i){  //这个找求x的过程建议结合图理解
             x=i;
             break;
         }
         int flag2=1;
         for(n=1;n<=t;n++){
             if(t%n==0){  //因为m*n=t；n首先得满足是t的因数
             m=t/n;
             y=n+m-b-x;

             memset(d,0,sizeof(d));
             for(int i=1;i<=n;i++){  //因为距离就是数的大小，所以我们验证在当前m,n,x,y下各个坐标到0的距离，即数的大小和个数保存在d中，和原数组做比较。
                 for(int j=1;j<=m;j++){
                     int temp=abs(i-x)+abs(j-y);
                     d[temp]++;   
                 }
             }
             int flag=1;
             for(int i=0;i<=b;i++){///这里i要从0开始比较，因为有可能出现多个"0"的情况.
                 if(a[i]!=d[i]){
                     flag=0;
                     break;
                 }
             }
             if(flag){
                 printf("%d %d\n",n,m);
                 printf("%d %d\n",x,y);
                 flag2=0;
                 break;
             }
             }
         }
         if(flag2)printf("-1\n");
    }

     return 0;
 }